Bạn đang xem Đề cương ôn tập học kỳ 2 Toán 11 năm 2021 – 2022 trường THPT Yên Hòa – Hà Nội. Cập nhật thêm đề thi thử, đề kiểm tra toán, học toán tại Toanpdf.com

TOANPDF.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp lớp 11 đề cương ôn tập học kỳ 2 Toán 11 năm học 2021 – 2022 trường THPT Yên Hòa – Hà Nội.ĐẠI SỐ VÀ GIẢI TÍCH 11:
1 DÃY SỐ – CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN:
+ Phương pháp chứng minh quy nạp.
+ Xác định một dãy số: Tìm các số hạng của một dãy số cho trước, tìm các số hạng của cấp số nhân, cấp số cộng.
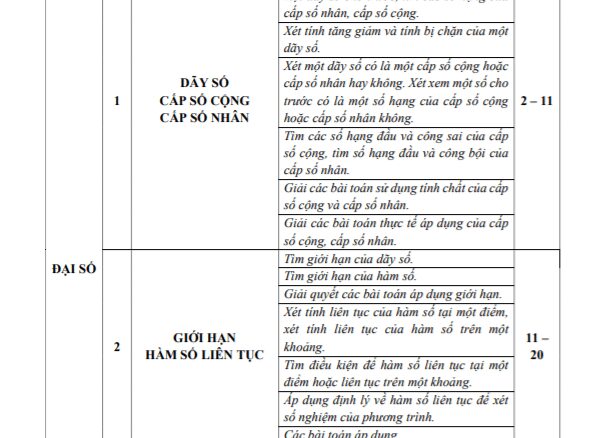
+ Xét tính tăng giảm và tính bị chặn của một dãy số.
+ Xét một dãy số có là một cấp số cộng hoặc cấp số nhân hay không. Xét xem một số cho trước có là một số hạng của cấp số cộng hoặc cấp số nhân không.
+ Tìm các số hạng đầu và công sai của cấp số cộng, tìm số hạng đầu và công bội của cấp số nhân.
+ Giải các bài toán sử dụng tính chất của cấp số cộng và cấp số nhân.
+ Giải các bài toán thực tế áp dụng của cấp số cộng, cấp số nhân.
2 GIỚI HẠN – HÀM SỐ LIÊN TỤC:
+ Tìm giới hạn của dãy số.
+ Tìm giới hạn của hàm số.
+ Giải quyết các bài toán áp dụng giới hạn.
+ Xét tính liên tục của hàm số tại một điểm, xét tính liên tục của hàm số trên một khoảng.
+ Tìm điều kiện để hàm số liên tục tại một điểm hoặc liên tục trên một khoảng.
+ Áp dụng định lý về hàm số liên tục để xét số nghiệm của phương trình.
+ Các bài toán áp dụng.
3 ĐẠO HÀM:
+ Tìm đạo hàm tại một điểm của hàm số.
+ Tìm đạo hàm trên một khoảng của hàm số.
+ Tìm điều kiện để hàm số có đạo hàm.
+ Tìm đạo hàm cấp cao của một hàm số.
+ Bài toán tiếp tuyến của đạo hàm.
+ Bài toán ứng dụng thực tế của đạo hàm.
+ Một số bài toán khác về đạo hàm của hàm số.
HÌNH HỌC 11:
4 VÉC TƠ TRONG KHÔNG GIAN – QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN:
+ Các bài toán về véc tơ trong không gian.
+ Chứng minh hai đường thẳng vuông góc.
+ Chứng minh đường thẳng vuông góc với mặt phẳng.
+ Chứng minh hai mặt phẳng vuông góc.
+ Bài toán về góc: Góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng; góc giữa hai mặt phẳng.
+ Bài toán về khoảng cách: Khoảng cách từ một điểm đến 1 đường thẳng; khoảng cách từ một điểm đến một mặt phẳng; khoảng cách từ một đường thẳng đến một mặt phẳng; khoảng cách giữa hai mặt phẳng; khoảng cách giữa hai đường thẳng chéo nhau.
+ Bài toán về giao điểm của một đường thẳng và một mặt phẳng; bài toán về giao tuyến của hai mặt phẳng; bài toán về thiết diện.
+ Một số bài toán áp dụng quan hệ vuông góc trong không gian.