Tài liệu gồm 61 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Giáo Viên Toán Việt Nam, tuyển tập các bài toán khối đa diện và thể tích khối đa diện trong các đề thi minh họa và đề thi chính thức THPT môn Toán của Bộ Giáo dục và Đào tạo giai đoạn từ năm 2017 đến năm 2021; các bài toán có đáp án và lời giải chi tiết. Tài liệu giúp học sinh lớp 12 tham khảo khi học chương trình Hình học 12 chương 1: Khối đa diện và thể tích khối đa diện và ôn thi tốt nghiệp THPT môn Toán.Trích dẫn tài liệu bài toán khối đa diện và thể tích trong đề thi THPT môn Toán của Bộ GD&ĐT (2017 – 2021):
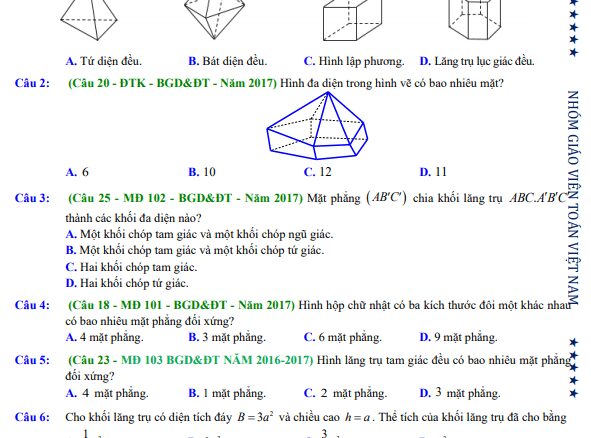
+ Mặt phẳng (AB’C’) chia khối lăng trụ ABC.A’B’C’ thành các khối đa diện nào?
A. Một khối chóp tam giác và một khối chóp ngũ giác. B. Một khối chóp tam giác và một khối chóp tứ giác. C. Hai khối chóp tam giác. D. Hai khối chóp tứ giác.
+ Cho hình chóp đều S ABCD có cạnh đáy bằng a, cạnh bên bằng 2a và O là tâm của đáy. Gọi M, N, P, Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác SAB, SBC, SCD, SDA và S’ là điểm đối xứng với S qua O. S’.MNPQ bằng?
+ Cho khối lăng trụ ABC.A’B’C’, khoảng cách từ C đến đường thẳng BB’ bằng 2, khoảng cách từ A đến các đường thẳng BB’ và CC’ lần lượt bằng 1 và 3, hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm M của B’C’ và A’M = 2. đã cho bằng?

Be the first to comment