Tài liệu gồm 59 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, tổng hợp tóm tắt lý thuyết, bài tập tự luận và bài tập trắc nghiệm chuyên đề Hàm Số Bậc Hai trong chương trình môn Kết Nối Tri Thức Với Cuộc Sống, có đáp án và lời giải chi tiết.I. TÓM TẮT LÝ THUYẾT.
1) Hàm số bậc hai có dạng 2 y ax bx c a b c a 0.
2) Khảo sát sự biến thiên của hàm số bậc hai:
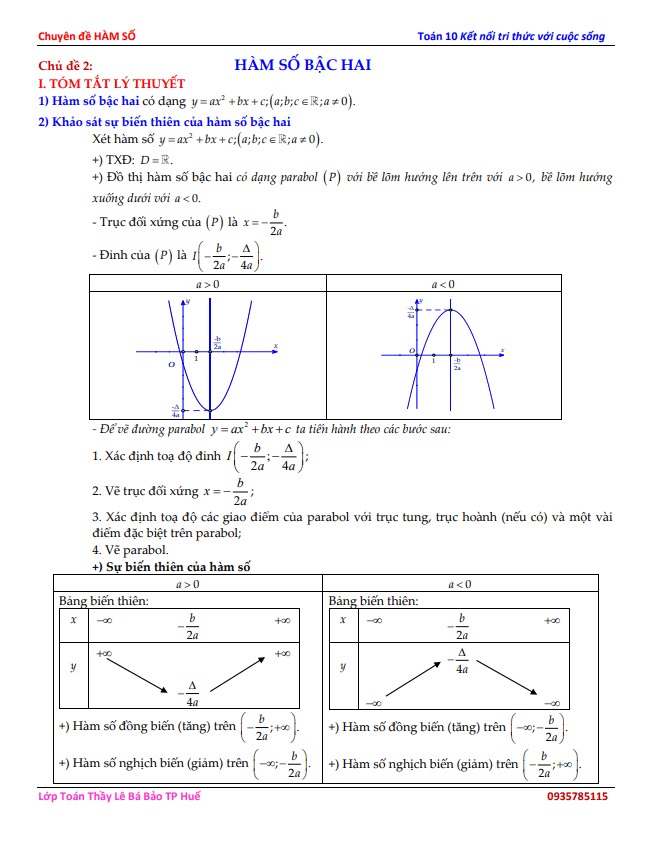
+ Xét hàm số 2 y ax bx c a b c a 0. + TXĐ: D. + Đồ thị hàm số bậc hai có dạng parabol P với bề lõm hướng lên trên với a 0 bề lõm hướng xuống dưới với a 0. Trục đối xứng của P là 2 b x a. Đỉnh của P là 2 4 b I a a.
+ Để vẽ đường parabol 2 y ax bx c ta tiến hành theo các bước sau: 1. Xác định toạ độ đỉnh 2 4 b I a a. 2. Vẽ trục đối xứng 2 b x a. 3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol. 4. Vẽ parabol.
+ Sự biến thiên của hàm số: a 0 a 0. Bảng biến thiên: x 2 b a y 4a. Hàm số đồng biến (tăng) trên 2 b a. Hàm số nghịch biến (giảm) trên 2 b a. Bảng biến thiên: x 2 b a y 4a. Hàm số đồng biến (tăng) trên 2 b a. Hàm số nghịch biến (giảm) trên 2 b a.
+ Nhận xét: Khi a 0: Hàm số có giá trị nhỏ nhất bằng 4a đạt được tại 2 b x a. Khi a 0: Hàm số có giá trị lớn nhất bằng 4a đạt được tại 2 b x a.
II. BÀI TẬP TỰ LUẬN.
III. BÀI TẬP TRẮC NGHIỆM.

Be the first to comment