Bạn đang xem Phương pháp nguyên hàm từng phần. Cập nhật thêm đề thi thử, đề kiểm tra toán, học toán tại Toanpdf.com

Bài viết hướng dẫn tìm nguyên hàm bằng phương pháp nguyên hàm từng phần, đây là dạng toán thường gặp trong chương trình Giải tích 12.I. KIẾN THỨC VẬN DỤNG
1. Định lí: Nếu $u = u(x)$ và $v = v(x)$ là hai hàm số có đạo hàm liên tục trên $K$ thì $int u dv = uv – int v du.$2. Phương pháp chung sử dụng phương pháp nguyên hàm từng phần tìm $int f (x)dx.$
+ Biến đổi $int f (x)dx = int p (x)q(x)dx$, $q(x)$ tìm nguyên hàm dễ hơn $p(x).$
+ Đặt $left{ {begin{array}{*{20}{l}}
{u = p(x)}\
{dv = q(x)dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = p'(x)dx}\
{v = Q(x)}
end{array}} right.$ với $Q(x)$ là một nguyên hàm của $q(x).$
+ $int f (x)dx$ $ = p(x)Q(x) – int Q (x)p'(x)dx.$3. Cách đặt $u$, $dv$ một số trường hợp hay gặp.
Trong bảng bưới đây ta có $p(x)$ là hàm đa thức.
Cách nhớ: Ưu tiên đặt $u$ theo câu: Nhất lô, nhì đa, tam lượng, tứ mũ.II. BÀI TẬP TRẮC NGHIỆM MINH HỌA
Ví dụ 1: Tìm nguyên hàm của hàm số $f(x) = (2x + 1){e^x}.$
A. $int {(2x + 1){e^x}dx} = (2x – 1){e^x} + C.$
B. $int {(2x + 1){e^x}dx} = (2x + 3){e^x} + C.$
C. $int {(2x + 1){e^x}dx} = (2x – 3){e^x} + C.$
D. $int {(2x + 1){e^x}dx} = (2x + 1){e^x} + C.$Lời giải:
Cách 1: Đặt $left{ {begin{array}{*{20}{l}}
{u = 2x + 1}\
{dv = {e^x}dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = 2dx}\
{v = {e^x}}
end{array}} right..$
Khi đó $int {(2x + 1){e^x}dx} $ $ = (2x + 1){e^x} – int 2 {e^x}dx.$
$ = (2x + 1){e^x} – 2{e^x} + C$ $ = (2x – 1){e^x} + C.$
Chọn đáp án A.
Cách 2: Sử dụng bảng: Ta theo dõi lại cách làm trên và bổ sung như sau:
Đặt $left{ {begin{array}{*{20}{l}}
{u = 2x + 1}\
{dv = {e^x}dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = 2dx}\
{v = {e^x}}
end{array}} right..$
Khi đó $int {(2x + 1){e^x}dx} $ $ = (2x + 1){e^x} – int {2{e^x}dx} .$
Đặt $left{ {begin{array}{*{20}{l}}
{u = 2}\
{dv = {e^x}dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = 0dx}\
{v = {e^x}}
end{array}} right..$
Khi đó $int 2 {e^x}dx = 2{e^x} + C.$
$ Rightarrow int {(2x + 1){e^x}dx} $ $ = (2x + 1){e^x} – 2{e^x} + int {0{e^x}dx} $ $ = (2x + 1){e^x} – 2{e^x} + C.$
Từ đó ta có thể trình bày nhanh theo bảng sau:$ Rightarrow int {(2x + 1){e^x}dx} $ $ = (2x + 1){e^x} – 2{e^x}$ $ + int {0{e^x}dx} $ $ = (2x + 1){e^x} – 2{e^x} + C.$
Chọn đáp án A.
Phân tích kết quả:
Cột trái lấy $u$ và đạo hàm đến khi bằng $0$ thì dừng lại.
Ta thấy kết quả bằng nhân chéo theo mũi tên lần 1 trừ nhân chéo theo mũi tên lần 2.
Tương tự nếu có nhiều mũi tên thì ta có kết quả tương tự: nhân chéo lần 1 trừ nhân chéo lần 2 cộng nhân chéo lần 3 trừ nhân chéo lần 4 ….Ví dụ 2: Tìm nguyên hàm của hàm số $f(x) = {x^2}{e^{ – x}}.$
A. $int {{x^2}} {e^{ – x}}dx = left( {{x^2} + 2x + 2} right){e^{ – x}} + C.$
B. $int {{x^2}} {e^{ – x}}dx = left( { – {x^2} + 2x – 2} right){e^{ – x}} + C.$
C. $int {{x^2}} {e^{ – x}}dx = left( {{x^2} – 2x + 2} right){e^{ – x}} + C.$
D. $int {{x^2}} {e^{ – x}}dx = left( { – {x^2} – 2x – 2} right){e^{ – x}} + C.$Lời giải:
Cách 1:
Đặt $left{ {begin{array}{*{20}{l}}
{u = {x^2}}\
{dv = {e^{ – x}}dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = 2xdx}\
{v = – {e^{ – x}}}
end{array}} right..$
Khi đó $int {{x^2}} {e^{ – x}}dx = – {x^2}{e^{ – x}} + int 2 x{e^{ – x}}dx.$
Đặt $left{ {begin{array}{*{20}{l}}
{u = 2x}\
{dv = {e^{ – x}}dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = 2dx}\
{v = – {e^{ – x}}}
end{array}} right..$
Khi đó $int 2 x{e^{ – x}}dx$ $ = – 2x{e^{ – x}} + int 2 {e^{ – x}}dx$ $ = – 2x{e^{ – x}} – 2{e^{ – x}} + C.$
$ Rightarrow int {{x^2}} {e^{ – x}}dx$ $ = – {x^2}{e^{ – x}} – 2x{e^{ – x}} – 2{e^{ – x}} + C$ $ = left( { – {x^2} – 2x – 2} right){e^{ – x}} + C.$
Chọn đáp án D.
Cách 2: Sử dụng bảng: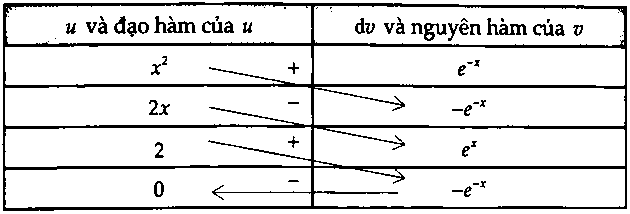$ Rightarrow int {{x^2}} {e^{ – x}}dx$ $ = – {x^2}{e^{ – x}} – 2x{e^{ – x}} – 2{e^{ – x}} + C$ $ = left( { – {x^2} – 2x – 2} right){e^{ – x}} + C.$
Chọn đáp án D.Ví dụ 3: Cho $int {(5x + 1){e^{ – x}}dx} $ $ = (mx + n){e^x} + C$ với $m$, $n$ là các số nguyên, $C$ là hằng số. Tính $S = 3m + n.$
A. $S=-15.$
B. $S=21.$
C. $S=-21.$
D. $S=15.$Lời giải:
Cách 1:
Đặt $left{ {begin{array}{*{20}{l}}
{u = 5x + 1}\
{dv = {e^{ – x}}dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = 5dx}\
{v = – {e^{ – x}}}
end{array}} right..$
Khi đó $int {(5x + 1){e^{ – x}}dx} $ $ = – (5x + 1){e^{ – x}} + int {5{e^{ – x}}} .$
$ = – (5x + 1){e^{ – x}} – 5{e^{ – x}} + C$ $ = ( – 5x – 6){e^{ – x}} + C.$
$ Rightarrow m = – 5$, $n = – 6$ $ Rightarrow S = 3m + n = – 21.$
Chọn đáp án C.
Cách 2: Sử dụng bảng:$ Rightarrow int {{x^2}} {e^{ – x}}dx$ $ = – (5x + 1){e^{ – x}} – 5{e^{ – x}} + C$ $ = ( – 5x – 6){e^{ – x}} + C.$
Chọn đáp án C.Ví dụ 4: Cho $int {(3x + 2){e^{ – 2x}}dx} $ $ = (mx + n){e^x} + C$ với $m$, $n$ là các số hữu tỉ, $C$ là hằng số. Tính $S = m – n.$
A. $S=-10.$
B. $S = frac{1}{4}.$
C. $S = frac{5}{4}.$
D. $S=10.$Lời giải:
Sử dụng bảng:$ Rightarrow int {(3x + 2){e^{ – 2x}}dx} $ $ = – frac{1}{2}(3x + 2){e^{ – 2x}} – frac{3}{4}{e^{ – 2x}} + C$ $ = left( { – frac{3}{2}x – frac{7}{4}} right){e^{ – 2x}} + C.$
$ Rightarrow m = – frac{3}{2}$, $n = – frac{7}{4}$ $ Rightarrow S = m – n = frac{1}{4}.$
Chọn đáp án B.Ví dụ 5: Cho $int {left( {{x^2} + x – 1} right){e^x}dx} $ $ = left( {m{x^2} + nx + p} right){e^x} + C$ với $m$, $n$, $p$ là các số nguyên, $C$ là hằng số. Tính $S = m + n + p.$
A. $S=2.$
B. $S=0.$
C. $S=-2.$
D. $S=3.$Lời giải:
Sử dụng bảng:$int {left( {{x^2} + x – 1} right){e^x}dx} $ $ = left( {{x^2} + x – 1} right){e^x}$ $ – (2x + 1){e^x} + 2{e^x} + C$ $ = left( {{x^2} – x} right){e^x} + C.$
$ Rightarrow m = 1$, $n = – 1$, $p = 0$ $ Rightarrow S = m + n + p = 0.$
Chọn đáp án B.Ví dụ 6: Cho $F(x) = frac{1}{4}{x^4} + frac{1}{3}{x^3}$ là một nguyên hàm của hàm số $xf(x).$ Tìm nguyên hàm của hàm số $f'(x){e^x}.$
A. $int {f’} (x){e^x}dx = (2x – 1){e^x} + C.$
B. $int {f’} (x){e^x}dx = (2x + 1){e^x} + C.$
C. $int {f’} (x){e^x}dx = (2x – 3){e^x} + C.$
D. $int {f’} (x){e^x}dx = (2x + 3){e^x} + C.$Lời giải:
Ta có $F(x) = frac{1}{4}{x^4} + frac{1}{3}{x^3}$ $ Rightarrow F'(x) = {x^3} + {x^2}.$
Theo đề bài suy ra $F'(x) = xf(x)$ $ Rightarrow f(x) = {x^2} + x$ $ Rightarrow f'(x) = 2x + 1.$
Suy ra $int {f’} (x){e^x}dx = int {(2x + 1){e^x}dx.} $
Đặt $left{ {begin{array}{*{20}{l}}
{u = 2x + 1}\
{dv = {e^x}}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = 2dx}\
{v = {e^x}}
end{array}} right..$
$ Rightarrow int {f’} (x){e^x}dx$ $ = int {(2x + 1){e^x}dx} $ $ = (2x + 1){e^x} – 2int {{e^x}} dx$ $ = (2x + 1){e^x} – 2{e^x} + C.$
$ = (2x – 1){e^x} + C.$
Chọn đáp án A.Ví dụ 7: Cho $F(x) = {x^3} + frac{1}{x}$ là một nguyên hàm của hàm số $frac{{ – 1}}{{{x^2}}} + xf(x).$ Tìm nguyên hàm của hàm số $f(x){e^{ – x}}.$
A. $int f (x){e^{ – x}}dx = – 3x{e^{ – x}} + 3{e^{ – x}} + C.$
B. $int f (x){e^{ – x}}dx = – 3x{e^{ – x}} – 3{e^{ – x}} + C.$
C. $int f (x){e^{ – x}}dx = 3x{e^{ – x}} – 3{e^{ – x}} + C.$
D. $int f (x){e^{ – x}}dx = 3x{e^{ – x}} + 3{e^{ – x}} + C.$Lời giải:
Ta có $F(x) = {x^3} + frac{1}{x}$ $ Rightarrow F'(x) = 3{x^2} – frac{1}{{{x^2}}}.$
Theo đề suy ra $F'(x) = – frac{1}{{{x^2}}} + xf(x)$ $ Rightarrow – frac{1}{{{x^2}}} + 3{x^2} = – frac{1}{{{x^2}}} + xf(x)$ $ Rightarrow f(x) = 3x.$
Suy ra $int f (x){e^{ – x}}dx = int 3 x{e^{ – x}}dx.$
Đặt $left{ {begin{array}{*{20}{l}}
{u = 3x}\
{dv = {e^{ – x}}}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = 3dx}\
{v = – {e^{ – x}}}
end{array}} right..$
$ Rightarrow int f (x){e^{ – x}}dx$ $ = int 3 x{e^{ – x}}dx = – 3x{e^{ – x}} + 3int {{e^{ – x}}} dx$ $ = – 3x{e^{ – x}} – 3{e^{ – x}} + C.$
Chọn đáp án B.Ví dụ 8: Cho $F(x) = (x – 1){e^x}$ là một nguyên hàm của hàm số $f(x){e^{2x}}.$ Tìm nguyên hàm của hàm số $f'(x){e^{2x}}.$
A. $int {f’} (x){e^{2x}}dx = (x – 2){e^x} + C.$
B. $int {f’} (x){e^{2x}}dx = frac{{2 – x}}{2}{e^x} + C.$
C. $int {f’} (x){e^{2x}}dx = (2 – x){e^x} + C.$
D. $int {f’} (x){e^{2x}}dx = (4 – 2x){e^x} + C.$Lời giải:
Ta có $F(x) = (x – 1){e^x}$ $ Rightarrow F'(x) = x{e^x}.$
Theo đề suy ra $F'(x) = f(x){e^{2x}}$ $ Rightarrow x{e^x} = f(x){e^{2x}}.$
$ Rightarrow f(x) = x{e^{ – x}}$ $ Rightarrow f'(x) = (1 – x){e^{ – x}}.$
$int {f’} (x){e^{2x}}dx$ $ = int {(1 – x){e^x}dx} .$
Đặt $left{ {begin{array}{*{20}{l}}
{u = 1 – x}\
{dv = {e^x}dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = – dx}\
{v = {e^x}}
end{array}} right..$
$ Rightarrow int {f’} (x){e^{2x}}dx$ $ = (1 – x){e^x} + int {{e^x}} dx$ $ = (1 – x){e^x} + {e^x} + C$ $ = (2 – x){e^x} + C.$
Chọn đáp án C.Ví dụ 9: Tìm nguyên hàm của hàm số $f(x) = (3x + 5)sin x.$
A. $int {(3x + 5)} sin xdx$ $ = – (3x + 5)cos x + 3sin x + C.$
B. $int {(3x + 5)} sin xdx$ $ = (3x + 5)cos x – 3sin x + C.$
C. $int {(3x + 5)} sin xdx$ $ = – (3x + 5)sin x + 3cos x + C.$
D. $int {(3x + 5)} sin xdx$ $ = (3x + 5)sin x – 3cos x + C.$Lời giải:
Cách 1:
Đặt $left{ {begin{array}{*{20}{l}}
{u = 3x + 5}\
{dv = sin xdx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = 3dx}\
{v = – cos x}
end{array}} right..$
Khi đó $int {(3x + 5)} sin xdx$ $ = – (3x + 5)cos x – int {( – 3cos x)dx} .$
$ = – (3x + 5)cos x + 3sin x + C.$
Chọn đáp án A.
Cách 2: Sử dụng bảng:$int {(3x + 5)} sin xdx$ $ = – (3x + 5)cos x + 3sin x + C.$
Chọn đáp án A.Ví dụ 10: Cho $int {(2x + 1)} sin 3xdx$ $ = (mx + n)cos 3x + psin 3x + C$ với $m$, $n$, $p$ là các số hữu tỉ, $C$ là hằng số. Tính $S = m – 2n + p.$
A. $S = frac{2}{9}.$
B. $S = frac{9}{2}.$
C. $S = frac{{11}}{9}.$
D. $S = frac{{11}}{2}.$Lời giải:
Sử dụng bảng:$ Rightarrow int {(2x + 1)} sin 3xdx$ $ = – (2x + 1)frac{1}{3}cos 3x + frac{2}{9}sin 3x + C.$
$ = left( { – frac{2}{3}x – frac{1}{3}} right)cos 3x + frac{2}{9}sin 3x + C.$
$ Rightarrow m = – frac{2}{3}$, $n = – frac{1}{3}$, $p = frac{2}{9}$ $ Rightarrow S = m – 2n + p = frac{2}{9}.$
Chọn đáp án A.Ví dụ 11: Cho $int {left( {{x^2} – x + 2} right)} sin xdx$ $ = left( {m{x^2} + nx + p} right)cos x$ $ + (qx + r)sin x + C$ với $m$, $n$, $p$, $q$ là các số nguyên, $C$ là hằng số. Tính $S = m + n + p + q + r.$
A. $S=0.$
B. $S=1.$
C. $S=2.$
D. $S=3.$Lời giải:
Sử dụng bảng:$int {left( {{x^2} – x + 2} right)} sin xdx$ $ = – left( {{x^2} – x + 2} right)cos x$ $ + (2x – 1)sin x$ $ + 2cos x + C.$
$ = left( { – {x^2} + x} right)cos x + (2x – 1)sin x + C$ $ Rightarrow m = – 1$, $n = 1$, $p = 0$, $q = 2$, $r = – 1.$
$ Rightarrow S = m + n + p + q + r = 1.$
Chọn đáp án B.Ví dụ 12: Cho $int {(3x + 4)} cos xdx$ $ = (mx + n)sin x + pcos x + C$ với $m$, $n$, $p$ là các số nguyên, $C$ là hằng số. Tính $S = m + n + p.$
A. $S=8.$
B. $S=9.$
C. $S=10.$
D. $S=11.$Lời giải:
Sử dụng bảng: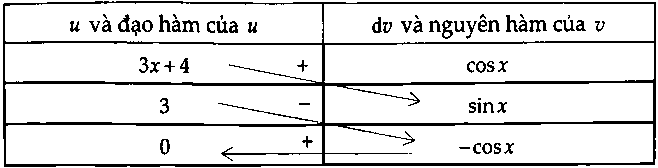$int {(3x + 4)} cos xdx$ $ = (3x + 4)sin x + 3cos x + C$ $ Rightarrow m = 3$, $n = 4$, $p = 3.$
$ Rightarrow S = m + n + p = 10.$
Chọn đáp án C.Ví dụ 13: Cho $int {(3x + 2)} cos 3xdx$ $ = (mx + n)sin 3x + pcos 3x + C$ với $m$, $n$, $p$ là các số hữu tỉ, $C$ là hằng số. Tính $S = m – n + p.$
A. $S=0.$
B. $S=1.$
C. $S=2.$
D. $S=3.$Lời giải:
Sử dụng bảng:$int {(3x + 4)} cos xdx$ $ = frac{1}{3}(3x + 2)sin 3x + frac{1}{3}cos 3x + C.$
$ = left( {x + frac{2}{3}} right)sin 3x + frac{1}{3}cos 3x + C.$
$ Rightarrow m = 1$, $n = frac{2}{3}$, $p = frac{1}{3}$ $ Rightarrow S = m + n + p = 2.$Ví dụ 14: Cho $int {left( {2{x^2} + x + 1} right)} cos 2xdx$ $ = left( {m{x^2} + nx + p} right)sin 2x$ $ + (qx + r)cos 2x + C$ với $m$, $n$, $p$, $q$ là các số hữu tỉ, $C$ là hằng số. Tính $S = m.n.p.q.r.$Lời giải:
Sử dụng bảng:$int {left( {2{x^2} + x + 1} right)} cos 2xdx$ $ = frac{1}{2}left( {2{x^2} + x + 1} right)sin 2x$ $ + frac{1}{4}(4x + 1)cos 2x$ $ – frac{1}{2}sin 2x + C.$
$ = left( {{x^2} + frac{1}{2}x} right)sin 2x$ $ + left( {x + frac{1}{4}} right)cos 2x + C$ $ Rightarrow m = 1$, $n = frac{1}{2}$, $p = 0$, $q = 1$, $r = frac{1}{4}.$
$ Rightarrow S = m.n.p.q.r = 0.$
Chọn đáp án B.Ví dụ 15: Cho $int {(2x – 5)} {cos ^2}xdx$ $ = left( {m{x^2} + nx} right)$ $ + (px + q)sin 2x$ $ + rcos 2x + C$ với $m$, $n$, $p$, $q$, $r$, $h$ là các số hữu tỉ, $C$ là hằng số. Tính $S = m + n + p + q + r.$
A. $S = – frac{5}{2}.$
B. $S = 0.$
C. $S = frac{5}{4}.$
D. $S = frac{5}{8}.$Lời giải: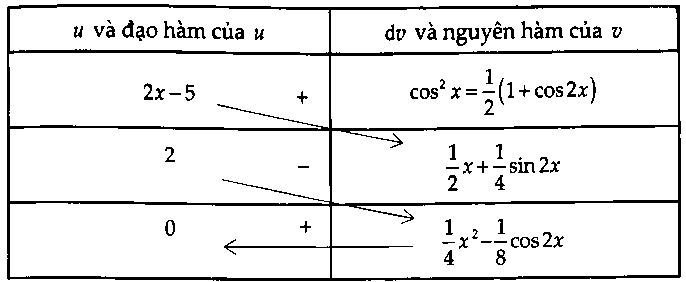$int {(2x – 5)} {cos ^2}xdx$ $ = (2x – 5)left( {frac{1}{2}x + frac{1}{4}sin 2x} right)$ $ – 2left( {frac{1}{4}{x^2} – frac{1}{8}cos 2x} right) + C.$
$ = left( {frac{{{x^2}}}{2} – frac{5}{2}x} right)$ $ + left( {frac{x}{2} – frac{5}{4}} right)sin 2x$ $ + frac{1}{4}cos 2x + C.$
$ Rightarrow m = frac{1}{2}$, $n = – frac{5}{2}$, $p = frac{1}{2}$, $q = – frac{5}{4}$, $r = frac{1}{4}.$
$ Rightarrow S = m + n + p + q + r = – frac{5}{2}.$
Chọn đáp án A.Ví dụ 16: Cho $int 1 6x{sin ^2}2xdx$ $ = m{x^2} + mxsin 4x$ $ + pcos 4x + C$ với $m$, $n$, $p$ là các số hữu tỉ, $C$ là hằng số. Tính $S= m.n.p.$
A. $S=-6.$
B. $S=4.$
C. $S=5.$
D. $S=8.$Lời giải:$int 1 6x{sin ^2}2xdx$ $ = 16xleft( {frac{1}{2}x – frac{1}{8}sin 4x} right)$ $ – 16left( {frac{1}{4}{x^2} + frac{1}{{32}}cos 4x} right) + C.$
$ = 4{x^2} – 2xsin 4x – frac{1}{2}cos 4x + C$ $ Rightarrow m = 4$, $n = – 2$, $p = – frac{1}{2}.$
$ Rightarrow S = m.n.p = 4.$
Chọn đáp án B.Ví dụ 17: Cho $int {frac{{2x + 1}}{{{{cos }^2}x}}} dx$ $ = (mx + n)tan x$ $ + pln |cos x| + C$ với $m$, $n$, $p$ là các số nguyên, $C$ là hằng số. Tính $S = m + n + p.$
A. $S=2.$
B. $S=3.$
C. $S=4.$
D. $S=5.$Lời giải:$int {frac{{2x + 1}}{{{{cos }^2}x}}dx} $ $ = (2x + 1)tan x$ $ + 2ln |cos x| + C.$
$ Rightarrow m = 2$, $n = 1$, $p = 2.$
$ Rightarrow S = m + n + p = 5.$
Chọn đáp án D.Ví dụ 18: Cho $int {frac{{9x + 2}}{{{{sin }^2}3x}}dx} $ $ = (mx + n)cot 3x$ $ + pln |sin 3x| + C$ với $m$, $n$, $p$ là các số hữu tỉ, $C$ là hằng số. Tính $S= m.n.p.$
A. $S=0.$
B. $S=2.$
C. $S=4.$
D. $S=6.$Lời giải:$int {frac{{9x + 2}}{{{{sin }^2}3x}}dx} $ $ = left( { – 3x – frac{2}{3}} right)cot 3x$ $ + ln |sin 3x| + C$ $ Rightarrow m = – 3$, $n = – frac{2}{3}$, $p = 1.$
$ Rightarrow S = m.n.p = 2.$
Chọn đáp án B.Ví dụ 19: Cho $int {sin } sqrt x dx$ $ = msqrt x cos sqrt x + nsin sqrt x + C$ với $m$, $n$ là các số nguyên, $C$ là hằng số. Trong mặt phẳng tọa độ $Oxy$, điểm $M(m;n)$ là đỉnh của parabol nào sau đây?
A. $y = {x^2} + 4x + 6.$
B. $y = – {x^2} – 4x + 1.$
C. $y = {x^2} + 4x + 3.$
D. $y = 2{x^2} + 8x + 3.$Lời giải:
Cách 1:
Đặt $left{ {begin{array}{*{20}{l}}
{u = 2sqrt x }\
{dv = frac{1}{{2sqrt x }}sin sqrt x dx = sin sqrt x d(sqrt x )}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{1}{{sqrt x }}dx}\
{v = – cos sqrt x }
end{array}} right..$
Khi đó $int {sin } sqrt x dx$ $ = int 2 sqrt x .frac{1}{{2sqrt x }}sin sqrt x dx$ $ = – 2sqrt x cos sqrt x + int {frac{1}{{sqrt x }}} cos sqrt x dx.$
$ = – 2sqrt x cos sqrt x $ $ + 2int {cos } sqrt x d(sqrt x )$ $ = – 2sqrt x cos sqrt x + 2sin sqrt x + C.$
$ Rightarrow m = – 2$, $n = 2$ $ Rightarrow M( – 2;2)$ là đỉnh của parabol $y = {x^2} + 4x + 6.$
Chọn đáp án A.
Cách 2: Sử dụng bảng: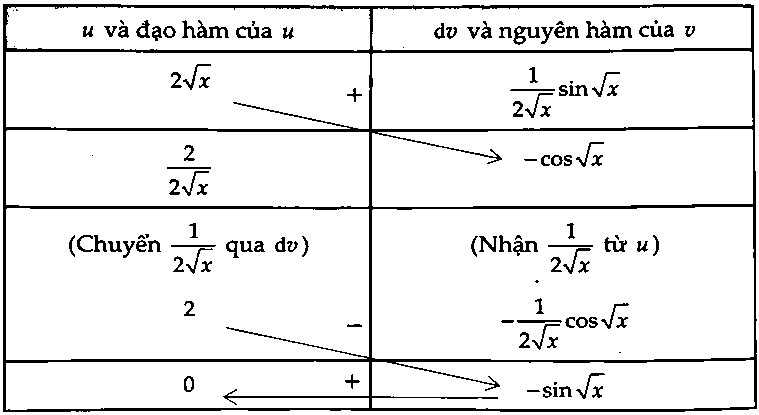$int {sin } sqrt x dx$ $ = int 2 sqrt x .frac{1}{{2sqrt x }}sin sqrt x dx$ $ = – 2sqrt x cos sqrt x + 2sin sqrt x + C.$
Chọn đáp án A.
Chú ý: Khi sử dụng bảng ta có thể dừng lại một bước nào đó chuyển một phần từ $u$ sang $dv$ hoặc ngược lại rồi làm tiếp.Ví dụ 20: Cho $int {sqrt x } sin sqrt x dx$ $ = (mx + n)cos sqrt x $ $ + psqrt x sin sqrt x + C$ với $m$, $n$, $p$ là các số nguyên, $C$ là hằng số. Trong hệ trục tọa độ $Oxyz$, điểm $M(m;n;p)$ thuộc mặt phẳng có phương trình nào sau đây?
A. $x + y – z + 2 = 0.$
B. $x – y – z – 2 = 0.$
C. $x + y = 0.$
D. $x + z = 0.$Lời giải:
$int {sqrt x } sin sqrt x dx$ $ = int 2 xfrac{1}{{2sqrt x }}sin sqrt x dx.$$int {sqrt x } sin sqrt x dx$ $ = – 2xcos sqrt x $ $ + 4sqrt x sin sqrt x $ $ + 4cos sqrt x + C.$
$ = ( – 2x + 4)cos sqrt x + 4sqrt x sin sqrt x + C$ $ Rightarrow m = – 2$, $n = 4$, $p = 4.$
$ Rightarrow M( – 2;4;4)$ thuộc mặt phẳng $x + y – z + 2 = 0.$
Chọn đáp án A.Ví dụ 21: Cho $F(x) = 2x{e^x}$ là một nguyên hàm của hàm số ${e^x}f(x).$ Tìm nguyên hàm của hàm số $f(x)sin x.$
A. $int f (x)sin xdx$ $ = (2x + 2)cos x – 2sin x + C.$
B. $int f (x)sin xdx$ $ = (2x + 2)cos x + 2sin x + C.$
C. $int f (x)sin xdx$ $ = – (2x + 2)cos x – 2sin x + C.$
D. $int f (x)sin xdx$ $ = – (2x + 2)cos x + 2sin x + C.$Lời giải:
Ta có $F(x) = 2x{e^x}$ $ Rightarrow F'(x) = 2{e^x} + 2x{e^x}.$
Theo đề suy ra $F'(x) = {e^x}f(x)$ $ Rightarrow f(x) = 2x + 2.$
Suy ra $int f (x)sin xdx$ $ = int {(2x + 2)} sin xdx.$
Đặt $left{ {begin{array}{*{20}{l}}
{u = 2x + 2}\
{dv = sin xdx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = 2dx}\
{v = – cos x}
end{array}} right..$
$ Rightarrow int f (x)sin xdx$ $ = – (2x + 2)cos x + 2int {cos xdx} $ $ = – (2x + 2)cos x + 2sin x + C.$
Chọn đáp án D.Ví dụ 22: Cho $F(x) = frac{1}{4}{x^4} – frac{1}{3}{x^3}$ là một nguyên hàm của hàm số $xf(x).$ Tìm nguyên hàm của hàm số $f'(x)cos x.$
A. $int {f’} (x)cos xdx$ $ = (2x – 1)sin x – 2cos x + C.$
B. $int {f’} (x)cos xdx$ $ = (2x – 1)sin x + 2cos x + C.$
C. $int {f’} (x)cos xdx$ $ = (1 – 2x)sin x + 2cos x + C.$
D. $int {f’} (x)cos xdx$ $ = (1 – 2x)sin x – 2cos x + C.$Lời giải:
Ta có $F(x) = frac{1}{4}{x^4} – frac{1}{3}{x^3}$ $ Rightarrow F'(x) = {x^3} – {x^2}.$
Theo đề suy ra $F'(x) = xf(x)$ $ Rightarrow f(x) = {x^2} – x$ $ Rightarrow f'(x) = 2x – 1.$
Suy ra $int {f’} (x)cos xdx$ $ = int {(2x – 1)} cos xdx.$
Đặt $left{ {begin{array}{*{20}{l}}
{u = 2x – 1}\
{dv = cos xdx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = 2dx}\
{v = sin x}
end{array}} right..$
$ Rightarrow int {f’} (x)cos xdx$ $ = (2x – 1)sin x – 2int {sin xdx} $ $ = (2x – 1)sin x + 2cos x + C.$
Chọn đáp án B.Ví dụ 23: Tính nguyên hàm của hàm số $f(x) = ln x$?
A. $int {ln xdx} = frac{{{{ln }^2}x}}{2} + C.$
B. $int {ln xdx} = frac{1}{x} + C.$
C. $int {ln xdx} = xln x – x + C.$
D. $int {ln xdx} = xln x + x + C.$Lời giải:
Cách 1: Đặt $left{ {begin{array}{*{20}{l}}
{u = ln x}\
{dv = dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{1}{x}dx}\
{v = x}
end{array}} right..$
Khi đó $int {ln xdx} = xln x – int d x$ $ = xln x – x + C.$
Chọn đáp án C.
Cách 2: Sử dụng bảng:$int {ln xdx} = xln x – int d x$ $ = xln x – x + C.$
Chọn đáp án C.Ví dụ 24: Cho $int {(4x + 2)} ln xdx$ $ = left( {m{x^2} + nx + p} right)ln x$ $ + q{x^2} + rx + C$ với $m$, $n$, $p$, $q$, $r$ là các số nguyên, $C$ là hằng số. Tính $S = m + n + p + q + r.$
A. $S = 1.$
B. $S=2.$
C. $S=7.$
D. $S=6.$Lời giải:$int {(4x + 2)} ln xdx$ $ = left( {2{x^2} + 2x} right)ln x$ $ – left( {{x^2} + 2x} right) + C.$
$ Rightarrow m = 2$, $n = 2$, $p = 0$, $q = – 1$, $r = – 2$ $ Rightarrow S = m + n + p + q + r = 1.$
Chọn đáp án A.Ví dụ 25: Cho $int x {ln ^2}xdx$ $ = frac{1}{m}{x^2}{ln ^2}x + frac{1}{n}{x^2}ln x$ $ + frac{1}{p}{x^2} + C$ với $m$, $n$, $p$ là các số nguyên, $C$ là hằng số. Tính $S=m+n-p.$
A. $S=0.$
B. $S=-4.$
C. $S=8.$
D. $S=4.$Lời giải:$int x {ln ^2}xdx$ $ = frac{{{x^2}}}{2}{ln ^2}x – frac{{{x^2}}}{2}ln x + frac{{{x^2}}}{4} + C$ $ Rightarrow m = 2$, $n = – 2$, $p = 4.$
$ Rightarrow S = m + n – p = – 4.$
Chọn đáp án B.Ví dụ 26: Cho $int {(6x + 1)} ln (x + 1)dx$ $ = left( {m{x^2} + nx} right)ln (x + 1)$ $ + p{x^2} + qx + rln (x + 1) + C$ với $m$, $n$, $p$, $q$, $r$ là các số hữu tỉ, $C$ là hằng số. Tính $S = m + n + p + q + r.$
A. $S = frac{3}{2}.$
B. $S = – frac{3}{2}.$
C. $S = frac{1}{2}.$
D. $S = frac{5}{2}.$Lời giải:$int {(6x + 1)} ln (x + 1)dx$ $ = left( {3{x^2} + x} right)ln (x + 1)$ $ – frac{{3{x^2}}}{2} + 2x – 2ln (x + 1) + C.$
$ Rightarrow m = 3$, $n = 1$, $p = – frac{3}{2}$, $q = 2$, $r = – 2$ $ Rightarrow S = m + n + p + q + r = frac{5}{2}.$
Chọn đáp án D.Ví dụ 27: Cho $F(x) = frac{1}{{2{x^2}}}$ là một nguyên hàm của hàm số $frac{{f(x)}}{x}.$ Tìm nguyên hàm của hàm số $f'(x)ln x.$
A. $int {f’} (x)ln xdx$ $ = – left( {frac{{ln x}}{{{x^2}}} + frac{1}{{2{x^2}}}} right) + C.$
B. $int {f’} (x)ln xdx$ $ = frac{{ln x}}{{{x^2}}} + frac{1}{{{x^2}}} + C.$
C. $int {f’} (x)ln xdx$ $ = – left( {frac{{ln x}}{{{x^2}}} + frac{1}{{{x^2}}}} right) + C.$
D. $int {f’} (x)ln xdx$ $ = frac{{ln x}}{{{x^2}}} + frac{1}{{2{x^2}}} + C.$Lời giải:
Ta có $F(x) = frac{1}{{2{x^2}}}$ $ Rightarrow F'(x) = – frac{1}{{{x^3}}}.$
Theo đề suy ra $F'(x) = frac{{f(x)}}{x}$ $ Rightarrow f(x) = – frac{1}{{{x^2}}}.$
Đặt $left{ {begin{array}{*{20}{l}}
{u = ln x}\
{dv = f'(x)dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{1}{x}dx}\
{v = f(x) = – frac{1}{{{x^2}}}}
end{array}} right..$
Đặt $left{ {begin{array}{*{20}{l}}
{u = ln x}\
{dv = f'(x)dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{1}{x}dx}\
{v = f(x) = – frac{1}{{{x^2}}}}
end{array}} right..$
$ Rightarrow int {f’} (x)ln xdx$ $ = – frac{{ln x}}{{{x^2}}} + int {frac{1}{{{x^3}}}dx} $ $ = – frac{{ln x}}{{{x^2}}} – frac{1}{{2{x^2}}} + C$ $ = – left( {frac{{ln x}}{{{x^2}}} + frac{1}{{2{x^2}}}} right) + C.$
Chọn đáp án A.Ví dụ 28: Cho $int {frac{{ln x}}{{{x^2}}}dx} = frac{a}{x}ln x + frac{b}{x} + C$ với $a$, $b$ là các số nguyên, $C$ là hằng số. Trong mặt phẳng tọa độ $Oxy$, điểm $M(a;b)$ nằm trên đồ thị hàm số nào sau đây?
A. $y=x.$
B. $y=2x+3.$
C. $y = {x^2}.$
D. $y=3x +1.$Lời giải: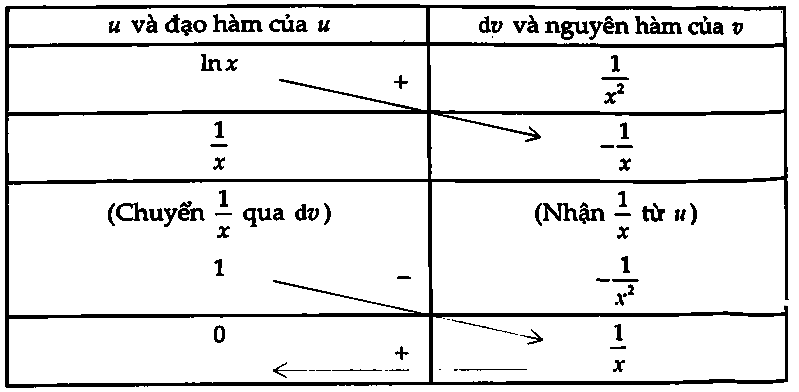$int {frac{{ln x}}{{{x^2}}}dx} $ $ = – frac{1}{x}ln x – frac{1}{x} + C$ $ Rightarrow a = – 1$, $b = – 1.$
$ Rightarrow M( – 1; – 1)$ thuộc đường thẳng $y = x.$
Chọn đáp án A.Ví dụ 29: Cho $int {frac{{1 + {x^2}}}{{{x^3}}}} ln xdx$ $ = frac{1}{m}{ln ^2}x + frac{1}{n}.frac{{ln x}}{{{x^2}}}$ $ + frac{1}{p}.frac{1}{{{x^2}}} + C$ với $m$, $n$, $p$ là các số nguyên, $C$ là hằng số. Trong không gian với hệ trục tọa độ $Oxyz$, tính khoảng cách $h$ từ điểm $M(m;n;p)$ đến gốc tọa độ.
A. $h = sqrt 6 .$
B. $h=2.$
C. $h = 2sqrt 6 .$
D. $h = 3sqrt 6 .$Lời giải:
Ta có $int {frac{{1 + {x^2}}}{{{x^3}}}} ln xdx$ $ = int {frac{{ln x}}{{{x^3}}}dx} + int {frac{{ln x}}{x}dx} .$
+ $int {frac{{ln x}}{x}dx} $ $ = int {ln xd(ln x)} = frac{{{{ln }^2}x}}{2} + {C_1}.$
+ Sử dụng bảng tính $int {frac{{ln x}}{{{x^3}}}dx.} $$ Rightarrow int {frac{{ln x}}{{{x^3}}}dx} $ $ = – frac{{ln x}}{{2{x^2}}} – frac{1}{{4{x^2}}} + {C_2}.$
$int {frac{{1 + x}}{{{x^2}}}} ln xdx$ $ = frac{{{{ln }^2}x}}{2} – frac{{ln x}}{{2{x^2}}} – frac{1}{{4{x^2}}} + C$ $ Rightarrow m = 2$, $n = – 2$, $p = – 4.$
$ Rightarrow M(2; – 2; – 4).$
$ Rightarrow h = OM$ $ = sqrt {{{(2 – 0)}^2} + {{( – 2 – 0)}^2} + {{( – 4 – 0)}^2}} $ $ = 2sqrt 6 .$
Chọn đáp án C.Ví dụ 30: Cho $F(x) = – frac{1}{{3{x^3}}}$ là một nguyên hàm của hàm số $frac{{f(x)}}{x}.$ Tìm nguyên hàm của hàm số $f'(x)ln x.$
A. $int {f’} (x)ln xdx = frac{{ln x}}{{{x^3}}} + frac{1}{{5{x^5}}} + C.$
B. $int {f’} (x)ln xdx = frac{{ln x}}{{{x^3}}} – frac{1}{{5{x^5}}} + C.$
C. $int {f’} (x)ln xdx = frac{{ln x}}{{{x^3}}} + frac{1}{{3{x^3}}} + C.$
D. $int {f’} (x)ln xdx = – frac{{ln x}}{{{x^3}}} + frac{1}{{3{x^3}}} + C.$Lời giải:
Ta có $F(x) = – frac{1}{{3{x^3}}}$ $ Rightarrow F'(x) = frac{{3{x^2}}}{{3{x^6}}} = frac{1}{{{x^4}}}.$
Theo đề suy ra $F'(x) = frac{{f(x)}}{x}$ $ Rightarrow f(x) = frac{1}{{{x^3}}}.$
Đặt $left{ {begin{array}{*{20}{l}}
{u = ln x}\
{dv = f'(x)dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{1}{x}dx}\
{v = f(x) = frac{1}{{{x^3}}}}
end{array}} right..$
$ Rightarrow int {f’} (x)ln xdx$ $ = frac{{ln x}}{{{x^3}}} – int {frac{1}{{{x^4}}}dx} $ $ = frac{{ln x}}{{{x^3}}} + frac{1}{{3{x^3}}} + C.$
Chọn đáp án C.