Tài liệu gồm 31 trang, được biên soạn bởi Nhóm Word – Biên Soạn Tài Liệu, hướng dẫn phương pháp giải bài toán xác định hệ số của hàm số nhất biến khi biết bảng biến thiên hoặc đồ thị; đây là dạng toán trắc nghiệm vận dụng – vận dụng cao (VD – VDC) thường xuất hiện trong chương trình Giải tích 12 chương 1 và đề thi tốt nghiệp Trung học Phổ thông Quốc gia môn Toán.Nội dung tài liệu xác định hệ số của hàm số nhất biến khi biết bảng biến thiên hoặc đồ thị:
A. BÀI TẬP MẪU
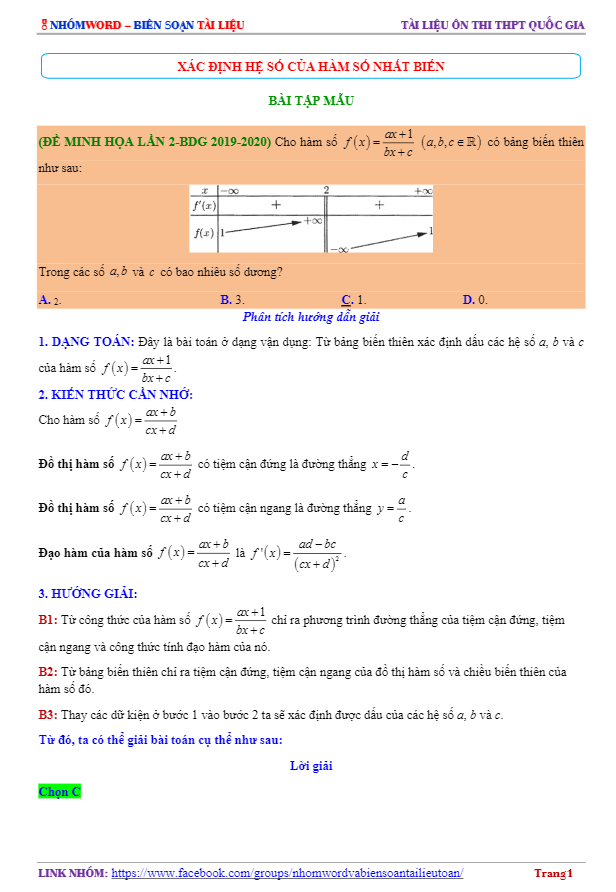
Cho hàm số f(x) = (ax + 1)/(bx + c) có bảng biến thiên như sau. Trong các số a, b và c có bao nhiêu số dương?
B. PHÂN TÍCH HƯỚNG DẪN GIẢI
1. Dạng toán: Đây là bài toán ở dạng vận dụng. Từ bảng biến thiên xác định dấu các hệ số a, b và c của hàm số f(x) = (ax + 1)/(bx + c).
2. Kiến thức cần nhớ:
Cho hàm số y = (ax + b)/(cx + d). Ta có:
+ Đồ thị hàm số y = (ax + b)/(cx + d) có tiệm cận đứng là đường thẳng x = -d/c.
+ Đồ thị hàm số y = (ax + b)/(cx + d) có tiệm cận ngang là đường thẳng y = a/c.
+ Đạo hàm của hàm số y = (ax + b)/(cx + d) là y’ = (ad – bc)/(cx + d)^2.
3. Hướng giải:
+ Bước 1: Từ công thức của hàm số f(x) = (ax + 1)/(bx + c) chỉ ra phương trình đường thẳng của tiệm cận đứng, tiệm cận ngang và công thức tính đạo hàm của nó.
+ Bước 2: Từ bảng biến thiên chỉ ra tiệm cận đứng, tiệm cận ngang của đồ thị hàm số và chiều biến thiên của hàm số đó.
+ Bước 3: Thay các dữ kiện ở bước 1 vào bước 2 ta sẽ xác định được dấu của các hệ số a, b và c.
C. BÀI TẬP TƯƠNG TỰ VÀ PHÁT TRIỂN
[ads]
Xem thêm:
+
+

Be the first to comment