Bạn đang xem Chuyên đề hàm số và đồ thị dành cho học sinh trung bình – yếu – Dương Minh Hùng. Cập nhật thêm đề thi thử, đề kiểm tra toán, học toán tại Toanpdf.com

Tài liệu gồm 148 trang, được biên soạn bởi thầy giáo Dương Minh Hùng, hướng dẫn giải các bài toán trắc nghiệm thuộc chuyên đề hàm số và đồ thị, dành cho học sinh trung bình – yếu, ôn thi THPT Quốc gia môn Toán năm học 2020 – 2021.Bài 1. Sự đồng biến và nghịch biến của hàm số.
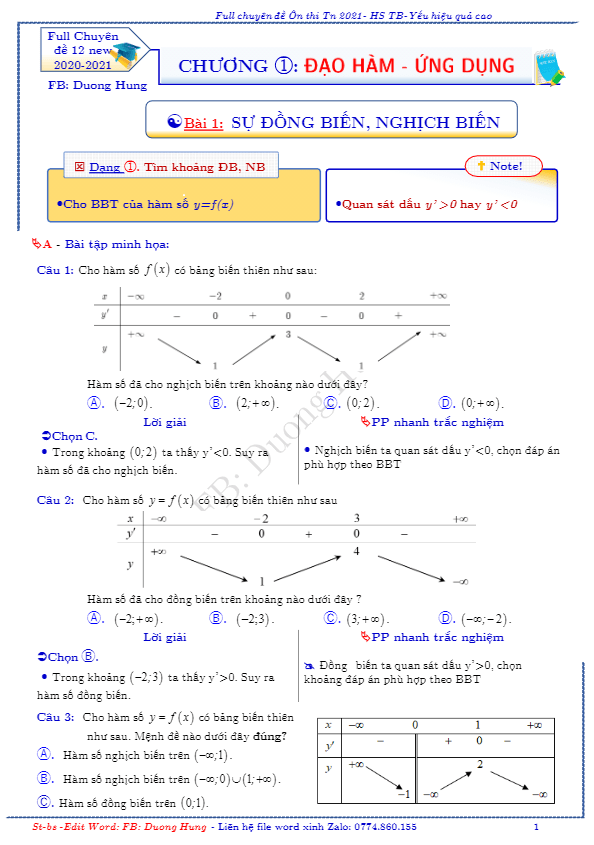
+ Dạng toán 1. Đề bài cho bảng biến thiên của hàm số y = f(x).
+ Dạng toán 2. Đề bài cho đồ thị của hàm số y = f(x).
+ Dạng toán 3. Đề bài cho hàm số y = f(x) tường minh.
+ Dạng toán 4. Đề bài cho hàm số y = f'(x).
+ Dạng toán 5. Đề bài cho đồ thị hàm số y = f'(x).
+ Dạng toán 6. Bài toán đồng biến / nghịch biến của hàm số chứa tham số.
Bài 2. Cực trị của hàm số.
+ Dạng toán 1. Tìm cực trị của hàm số.
+ Dạng toán 2. Đề bài cho đồ thị của hàm số y = f(x).
+ Dạng toán 3. Đề bài cho hàm số y = f(x) tường minh.
+ Dạng toán 4. Đề bài cho đồ thị hàm số y = f'(x).
+ Dạng toán 5. Tìm tham số m để hàm số đạt cực trị tại điểm cho trước.
+ Dạng toán 6. Tìm tham số m để hàm số bậc ba có cực trị thỏa điều kiện.
+ Dạng toán 7. Tìm tham số m để hàm số trùng phương có cực trị thỏa điều kiện.
Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
+ Dạng toán 1. Đề bài cho đồ thị của hàm số y = f(x).
+ Dạng toán 2. Đề bài cho bảng biến thiên của hàm số y = f(x).
+ Dạng toán 3. Đề bài cho đồ thị của hàm số y = f'(x).
+ Dạng toán 4. Tìm GTLN – GTNN của hàm số trên đoạn [a;b].
+ Dạng toán 5. Tìm GTLN – GTNN của hàm số trên khoảng (a;b).
+ Dạng toán 6. Tìm tham số m để hàm số đạt GTLN – GTNN bằng k.
+ Dạng toán 7. Ứng dụng GTLN – GTNN vào phương trình, bất phương trình chứa tham số.
Bài 4. Đường tiệm cận của đồ thị hàm số.
+ Dạng toán 1. Tìm tiệm cận bằng định nghĩa, bảng biến thiên hoặc đồ thị.
+ Dạng toán 2. Tìm số tiệm cận của những hàm số tường minh thường gặp.
+ Dạng toán 3. Tìm giá trị của tham số để đồ thị hàm số có số tiệm cận thỏa điều kiện.
Bài 5. Đồ thị hàm số bậc ba.
+ Dạng toán 1. Nhận dạng hàm số bậc ba khi cho đồ thị hàm số.
+ Dạng toán 2. Biện luận số nghiệm của phương trình bằng đồ thị hàm số.
+ Dạng toán 3. Sự tương giao của hai đồ thị (liên quan đến tọa độ giao điểm).
+ Dạng toán 4. Xác định hệ số a, b, c, d từ đồ thị hàm số bậc ba.
Bài 6. Đồ thị hàm số trùng phương.
+ Dạng toán 1. Nhận dạng hàm số trùng phương khi cho đồ thị hàm số.
+ Dạng toán 2. Biện luận số nghiệm của phương trình bằng đồ thị hàm số.
+ Dạng toán 3. Sự tương giao của hai đồ thị (liên quan đến tọa độ giao điểm).
+ Dạng toán 4. Xác định hệ số a, b, c từ đồ thị hàm trùng phương.
Bài 7. Đồ thị hàm số phân thức hữu tỉ.
+ Dạng toán 1. Nhận dạng hàm số phân thức hữu tỉ khi cho đồ thị hàm số.
+ Dạng toán 2. Sự tương giao của hai đồ thị (liên quan đến tọa độ giao điểm).
+ Dạng toán 3. Xác định hệ số a, b, c, d từ đồ thị hàm số hữu tỷ.
+ Dạng toán 4. Tìm điều kiện tham số m thỏa điều kiện cho trước.
Bài 8. Tiếp tuyến của đồ thị hàm số.
+ Dạng toán 1. Tiếp tuyến tại tiếp điểm của đồ thị.
+ Dạng toán 2. Tiếp tuyến của đồ thị biết hệ số góc k.
+ Dạng toán 3. Bài toán tìm tham số m, diện tích tam giác.Xem thêm: