Tài liệu gồm 126 trang, được biên soạn bởi thầy giáo Diệp Tuân, tổng hợp lý thuyết, phân dạng toán và chọn lọc bài tập cực trị của hàm số, giúp học sinh học tốt chương trình Giải tích 12 chương 1: .A. LÝ THUYẾT
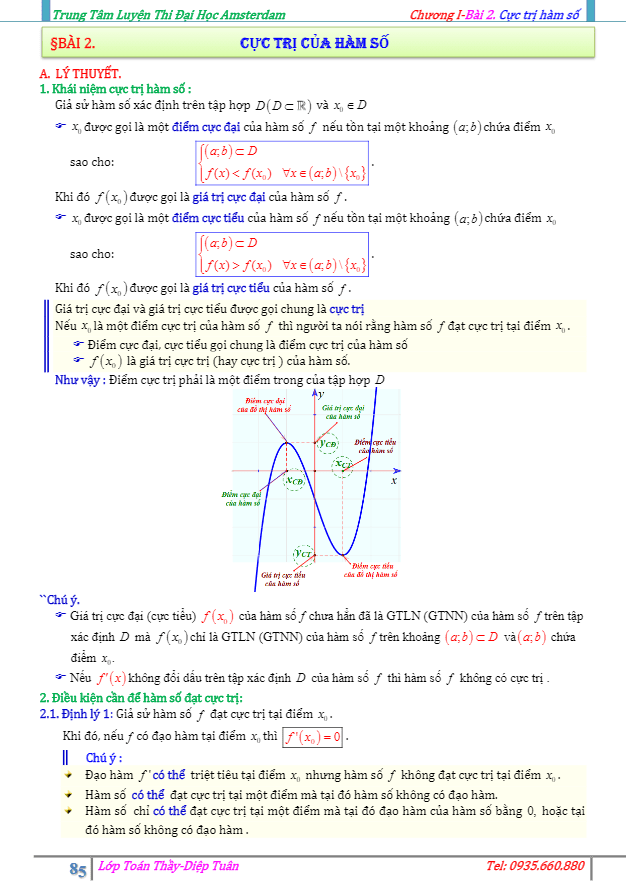
1. Khái niệm cực trị hàm số.
2. Điều kiện cần để hàm số đạt cực trị.
3. Điều kiện đủ để hàm số đạt cực trị.
B. PHƯƠNG PHÁP GIẢI TOÁN
Dạng toán 1. Tìm các điểm cực trị của hàm số.
Dạng toán 2. Định tham số m để hàm số f(x) đạt cực trị.
+ Loại 1. Định tham số m để hàm số f(x) đạt cực trị tại điểm x0 cho trước.
+ Loại 2. Định tham số m để hàm số f(x) có cực trị (không có điều kiện).
+ Loại 3. Định tham số m để hàm số f(x) có cực trị thỏa mãn điều kiện cho trước (có điều kiện).
[ads]
Dạng toán 3. Ứng dụng cực trị giải phương trình, bất phương trình, hệ phương trình đại số.
Dạng toán 4. Xác định cực trị của hàm hợp y = f(u(x)) khi biết đồ thị, bảng biến thiên của f(x), f'(x).
Dạng toán 5. Cực trị của hàm số trị tuyệt đối.
+ Loại 1. Cho hàm số y = f(x) có số điểm cực trị a, suy ra số điểm cực trị của hàm số y = |f(x)| hoặc y = |f(x ± a)|.
+ Loại 2. Cho hàm số y = f(x) có số điểm cực trị dương a, suy ra số điểm cực trị của y = f(|x|).
+ Loại 3. Số điểm cực trị của hàm số y = f(|ax + b| + c|) bằng 2k + 1.Bài tập trong mỗi dạng toán được chia thành các mức độ nhận thức: nhận biết (NB), thông hiểu (TH), vận dụng (VD) và vận dụng cao (VDC).Xem thêm:

Be the first to comment