
Bài viết hướng dẫn phương pháp giải và biện luận các dạng phương trình lượng giác cơ bản trong chương trình Đại số và Giải tích 11.I. PHƯƠNG PHÁP GIẢI VÀ BIỆN LUẬN CÁC DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
Bài toán 1: Giải và biện luận phương trình: $sin x = m.$
PHƯƠNG PHÁP CHUNG: Ta biện luận theo các bước sau:
Bước 1: Nếu $|m| > 1$ phương trình vô nghiệm.
Bước 2: Nếu $|m| le 1$, xét hai khả năng:
+ Khả năng 1: Nếu $m$ được biểu diễn qua $sin $ của góc đặc biệt, giả sử $alpha $, khi đó phương trình có dạng:
$sin x = sin alpha $ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = alpha + 2kpi }\
{x = pi – alpha + 2kpi }
end{array}} right.$, $k in Z.$
+ Khả năng 2: Nếu $m$ không biểu diễn được qua $sin $ của góc đặc biệt, khi đó đặt $m = sin alpha $, ta được:
$sin x = sin alpha $ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = alpha + 2kpi }\
{x = pi – alpha + 2kpi }
end{array}} right.$, $k in Z.$
Trong cả hai trường hợp ta đều kết luận phương trình có hai họ nghiệm.
Đặc biệt:
$sin x = 0 Leftrightarrow x = kpi $, $k in Z.$
$sin x = 1 Leftrightarrow x = frac{pi }{2} + 2kpi $, $k in Z.$
$sin x = – 1 Leftrightarrow x = – frac{pi }{2} + 2kpi $, $k in Z.$Ví dụ 1: Giải các phương trình sau:
a. $sin x = frac{1}{3}.$
b. $sin left( {2x – frac{pi }{4}} right) + sin left( {3x + frac{pi }{3}} right) = 0.$a. Đặt $frac{1}{3} = sin alpha $, khi đó:
$sin x = sin alpha $ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = alpha + 2kpi }\
{x = pi – alpha + 2kpi }
end{array}} right.$, $k in Z.$
Vậy phương trình có hai họ nghiệm.
b. Ta có: $sin left( {2x – frac{pi }{4}} right) + sin left( {3x + frac{pi }{3}} right) = 0$ $ Leftrightarrow sin left( {2x – frac{pi }{4}} right) = – sin left( {3x + frac{pi }{3}} right)$ $ Leftrightarrow sin left( {2x – frac{pi }{4}} right) = sin left( { – 3x – frac{pi }{3}} right)$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{2x – frac{pi }{4} = – 3x – frac{pi }{3} + 2kpi }\
{2x – frac{pi }{4} = pi – left( { – 3x – frac{pi }{3}} right) + 2kpi }
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = – frac{pi }{{60}} + frac{{2kpi }}{5}}\
{x = – frac{{19pi }}{{12}} – 2kpi }
end{array}} right.$, $k in Z.$
Vậy phương trình có hai họ nghiệm.Ví dụ 2: Giải phương trình: $sin (pi sin 2x) = 1.$Ta có: $sin (pi sin 2x) = 1$ $ Leftrightarrow pi sin 2x = frac{pi }{2} + 2kpi $ $ Leftrightarrow sin 2x = frac{1}{2} + 2k$, $k in Z$ $(1).$
Phương trình $(1)$ có nghiệm khi và chỉ khi:
$left| {frac{1}{2} + 2k} right| le 1$ $ Leftrightarrow – frac{3}{4} le k le frac{1}{4}$ $ Leftrightarrow k = 0.$
Khi đó $(1)$ có dạng:
$sin 2x = frac{1}{2}$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{2x = frac{pi }{6} + 2lpi }\
{2x = frac{{5pi }}{6} + 2lpi }
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = frac{pi }{{12}} + lpi }\
{x = frac{{5pi }}{{12}} + lpi }
end{array}} right.$, $l in Z.$
Vậy phương trình có hai họ nghiệm.Bài toán 2: Giải và biện luận phương trình: $cos x = m.$
PHƯƠNG PHÁP CHUNG: Ta biện luận theo các bước sau:
Bước 1: Nếu $|m| > 1$ thì phương trình vô nghiệm.
Bước 2: Nếu $|m| le 1$, xét hai trường hợp:
+ Khả năng 1: Nếu $m$ được biểu diễn qua $cos $ của góc đặc biệt, giả sử $alpha $, khi đó phương trình có dạng:
$cos x = cos alpha $ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = alpha + 2kpi }\
{x = – alpha + 2kpi }
end{array}} right.$, $k in Z.$
+ Khả năng 2: Nếu $m$ không biểu diễn được qua $cos $ của góc đặc biệt, khi đó đặt $m = cos alpha $, ta được:
$cos x = cos alpha $ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{x = alpha + 2kpi }\
{x = – alpha + 2kpi }
end{array}} right.$, $k in Z.$
Trong cả hai trường hợp ta đều kết luận phương trình có hai họ nghiệm.
Đặc biệt:
$cos x = 0 Leftrightarrow x = frac{pi }{2} + kpi $, $k in Z.$
$cos x = 1 Leftrightarrow x = 2kpi $, $k in Z.$
$cos x = – 1 Leftrightarrow x = pi + 2kpi $, $k in Z.$Ví dụ 3: Giải các phương trình sau:
a. $sin 3x = cos 2x.$
b. $cos left( {2x – frac{pi }{4}} right) + sin left( {x + frac{pi }{4}} right) = 0.$a. Ta có:
$sin 3x = cos 2x$ $ Leftrightarrow sin 3x = sin left( {frac{pi }{2} – 2x} right)$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{3x = frac{pi }{2} – 2x + 2kpi }\
{3x = pi – left( {frac{pi }{2} – 2x} right) + 2kpi }
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = frac{pi }{{10}} + frac{{2kpi }}{5}}\
{x = frac{pi }{2} + 2kpi }
end{array}} right.$, $k in Z.$
Vậy phương trình có hai họ nghiệm.
b. Ta có:
$cos left( {2x – frac{pi }{4}} right) + sin left( {x + frac{pi }{4}} right) = 0$ $ Leftrightarrow cos left( {2x – frac{pi }{4}} right) = – sin left( {x + frac{pi }{4}} right)$ $ Leftrightarrow cos left( {2x – frac{pi }{4}} right) = cos left( {x + frac{pi }{4} + frac{pi }{2}} right)$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{2x – frac{pi }{4} = x + frac{{3pi }}{4} + 2kpi }\
{2x – frac{pi }{4} = – x – frac{{3pi }}{4} + 2kpi }
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = pi + 2kpi }\
{x = – frac{pi }{6} + frac{{2kpi }}{3}}
end{array}} right.$, $k in Z.$
Vậy phương trình có hai họ nghiệm.Ví dụ 4: Giải phương trình: $cos left[ {frac{pi }{2}cos left( {x – frac{pi }{4}} right)} right] = frac{{sqrt 2 }}{2}.$Phương trình tương đương với:
$left[ {begin{array}{*{20}{l}}
{frac{pi }{2}cos left( {x – frac{pi }{4}} right) = frac{pi }{4} + 2kpi }\
{frac{pi }{2}cos left( {x – frac{pi }{4}} right) = – frac{pi }{4} + 2kpi }
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{cos left( {x – frac{pi }{4}} right) = frac{1}{2} + 4k:left( 1 right)}\
{cos left( {x – frac{pi }{4}} right) = – frac{1}{2} + 4k:left( 2 right)}
end{array}} right.$, $k in Z.$|
Phương trình $(1)$ có nghiệm khi và chỉ khi:
$left| {frac{1}{2} + 4k} right| le 1$ $ Leftrightarrow – frac{3}{8} le k le frac{1}{8}$ $ Leftrightarrow k = 0.$
Khi đó $(1)$ có dạng:
$cos left( {x – frac{pi }{4}} right) = frac{1}{2}$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x – frac{pi }{4} = frac{pi }{3} + 2lpi }\
{x – frac{pi }{4} = – frac{pi }{3} + 2lpi }
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = frac{{7pi }}{{12}} + 2lpi }\
{x = – frac{pi }{{12}} + 2lpi }
end{array}} right.$, $l in Z$ $(3).$
Phương trình $(2)$ có nghiệm khi và chỉ khi:
$left| { – frac{1}{2} + 4k} right| le 1$ $ Leftrightarrow – frac{1}{8} le k le frac{3}{8}$ $ Leftrightarrow k = 0.$
Khi đó $(2)$ có dạng:
$cos left( {x – frac{pi }{4}} right) = – frac{1}{2}$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x – frac{pi }{4} = frac{{2pi }}{3} + 2lpi }\
{x – frac{pi }{4} = – frac{{2pi }}{3} + 2lpi }
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = frac{{11pi }}{{12}} + 2lpi }\
{x = – frac{{5pi }}{{12}} + 2lpi }
end{array}} right.$, $l in Z$ $(4).$
Kết hợp $(3)$ và $(4)$, ta được:
$left[ {begin{array}{*{20}{l}}
{x = frac{{11pi }}{{12}} + lpi }\
{x = frac{{7pi }}{{12}} + lpi }
end{array}} right.$, $l in Z.$
Vậy phương trình có hai họ nghiệm.Bài toán 3: Giải và biện luận phương trình: $tan x = m.$
PHƯƠNG PHÁP CHUNG: Ta biện luận theo các bước sau:
Đặt điều kiện:
$cos x ne 0 Leftrightarrow x ne frac{pi }{2} + kpi $, $k in Z.$
Xét hai khả năng:
+ Khả năng 1: Nếu $m$ được biểu diễn qua $tan $ của góc đặc biệt, giả sử $alpha $, khi đó phương trình có dạng:
$tan x = tan alpha $ $ Leftrightarrow x = alpha + kpi $, $k in Z.$
+ Khả năng 2: Nếu $m$ không biểu diễn được qua $tan $ của góc đặc biệt, khi đó đặt $m = tan alpha $, ta được:
$tan x = tan alpha $ $ Leftrightarrow x = alpha + kpi $, $k in Z.$
Trong cả hai trường hợp ta đều kết luận phương trình có một họ nghiệm.
Nhận xét: Như vậy với mọi giá trị của tham số phương trình luôn có nghiệm.Ví dụ 5: Giải phương trình: $tan left[ {frac{pi }{4}(cos x + sin x)} right] = 1.$Điều kiện: $cos left[ {frac{pi }{4}(cos x + sin x)} right] ne 0$ $(*).$
Phương trình tương đương với:
$frac{pi }{4}(cos x + sin x) = frac{pi }{4} + kpi $ $ Leftrightarrow cos x + sin x = 1 + 4k$, $k in Z$ $(1).$
Phương trình $(1)$ có nghiệm khi và chỉ khi:
$left| {1 + 4k} right| le sqrt 2 $ $ Leftrightarrow – frac{{sqrt 2 + 1}}{4} le k le frac{{sqrt 2 – 1}}{4}$ $ Leftrightarrow k = 0.$
Khi đó $(1)$ có dạng:
$cos x + sin x = 1$ $ Leftrightarrow sqrt 2 sin left( {x + frac{pi }{4}} right) = 1$ $ Leftrightarrow sin left( {x + frac{pi }{4}} right) = frac{{sqrt 2 }}{2}$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x + frac{pi }{4} = frac{pi }{4} + 2lpi }\
{x + frac{pi }{4} = frac{{3pi }}{4} + 2lpi }
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 2lpi }\
{x = frac{pi }{2} + 2lpi }
end{array}} right.$, $l in Z$ thoả mãn $(*).$
Vậy phương trình có hai họ nghiệm.Bài toán 4: Giải và biện luận phương trình: $cot x = m.$
PHƯƠNG PHÁP CHUNG: Ta biện luận theo các bước sau:
Đặt điều kiện:
$sin x ne 0 Leftrightarrow x ne kpi $, $k in Z.$
Xét hai khả năng:
+ Khả năng 1: Nếu $m$ được biểu diễn qua $cot $ của góc đặc biệt, giả sử $alpha $, khi đó phương trình có dạng:
$cot x = cot alpha Leftrightarrow x = alpha + kpi $, $k in Z.$
+ Khả năng 2: Nếu $m$ không biểu diễn được qua $cot $ của góc đặc biệt, khi đó đặt $m = cot alpha $, ta được:
$cot x = cot alpha Leftrightarrow x = alpha + kpi $, $k in Z.$
Trong cả hai trường hợp ta đều kết luận phương trình có một họ nghiệm.
Nhận xét: Như vậy với mọi giá trị của tham số phương trình luôn có nghiệm.Ví dụ 6: Giải các phương trình sau:
a. $cot left( {frac{pi }{4} – x} right) = frac{1}{{sqrt 3 }}.$
b. $cos x = sqrt 3 sin x.$a. Điều kiện:
$sin left( {frac{pi }{4} – x} right) ne 0$ $ Leftrightarrow frac{pi }{4} – x ne kpi $ $ Leftrightarrow x ne frac{pi }{4} – kpi $, $k in Z$ $(*).$
Ta có:
$cot left( {frac{pi }{4} – x} right) = cot frac{pi }{3}$ $ Leftrightarrow frac{pi }{4} – x = frac{pi }{3} + kpi $ $ Leftrightarrow x = – frac{pi }{{12}} – kpi $, $k in Z$ thoả mãn điều kiện $(*).$
Vậy phương trình có một họ nghiệm.
b. Ta có:
$cos x = sqrt 3 sin x$ $ Leftrightarrow cot x = sqrt 3 = cot frac{pi }{6}$ $ Leftrightarrow x = frac{pi }{6} + kpi $, $k in Z.$
Vậy phương trình có một họ nghiệm. Bài toán 5: Biện luận theo $m$ số nghiệm thuộc $(alpha ,beta )$ của phương trình lượng giác cơ bản.
PHƯƠNG PHÁP CHUNG: Giả sử với phương trình: $sin x = m.$
Ta lựa chọn một trong hai cách sau:
Cách 1: Thực hiện theo các bước sau:
+ Bước 1: Biểu diễn $(alpha ,beta )$ trên đường tròn đơn vị thành cung $widehat {AB}.$
+ Bước 2: Tịnh tiến đường thẳng $m$ song song với trục cosin, khi đó số giao điểm của nó với cung $widehat {AB}$ bằng số nghiệm thuộc $(alpha ,beta )$ của phương trình.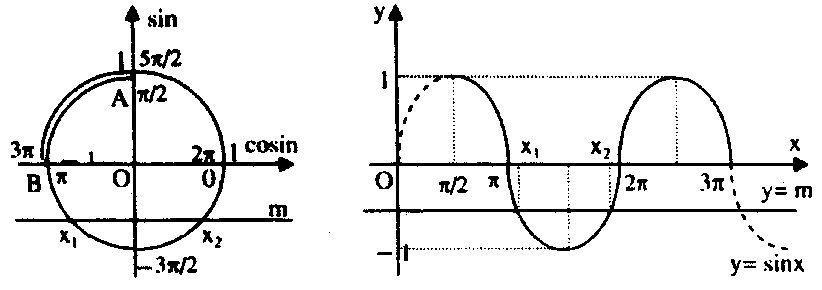 Cách 2: Thực hiện theo các bước sau:
Cách 2: Thực hiện theo các bước sau:
+ Bước 1: Vẽ đồ thị hàm số $y = sin x$, lấy trên $(alpha ,beta ).$
+ Bước 2: Tịnh tiến đường thẳng $y = m$ song song với trục $Ox$, khi đó số giao điểm của nó với phần đồ thị hàm số $y = sin x$ bằng số nghiệm thuộc $(alpha ,beta )$ của phương trình.
Chú ý: Phương pháp trên được mở rộng tự nhiên cho:
1. Phương trình $cos x = m$, với lưu ý khi sử dụng cách 1 ta tịnh tiến đường thẳng $m$ song song với trục sin.
2. Với các phương trình $tan x = m$ và $cot x = m$ ta chỉ có thể sử dụng cách 2.Ví dụ 7: Biện luận theo $m$ số nghiệm thuộc $left( {frac{pi }{6},frac{{8pi }}{3}} right)$ của phương trình $sin x = m.$Ta lựa chọn một trong hai cách biểu diễn: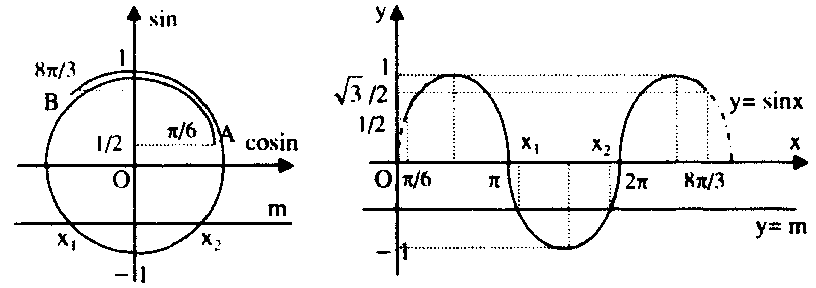 Kết luận: đặt $D = left( {frac{pi }{6},frac{{8pi }}{3}} right)$, ta có:
Kết luận: đặt $D = left( {frac{pi }{6},frac{{8pi }}{3}} right)$, ta có:
+ Với $|m| > 1$, phương trình vô nghiệm.
+ Với $m =-1$, phương trình có một nghiệm thuộc $D.$
+ Với $ – 1 < m < frac{1}{2}$ hoặc $m=1$, phương trình có hai nghiệm phân biệt thuộc $D.$
+ Với $frac{1}{2} le m < frac{{sqrt 3 }}{2}$, phương trình có ba nghiệm phân biệt thuộc $D.$
+ Với $frac{{sqrt 3 }}{2} le m < 1$, phương trình có bốn nghiệm phân biệt thuộc $D.$Ví dụ 8: Biện luận theo $m$ số nghiệm thuộc $left( { – frac{{5pi }}{4},pi } right)$ của phương trình: $(m + 1)sin x = (m – 1)cos x$ $(1).$Biến đổi phương trình về dạng:
$sin x + cos x = m(cos x – sin x)$ $ Leftrightarrow sqrt 2 sin left( {x + frac{pi }{4}} right) = msqrt 2 cos left( {x + frac{pi }{4}} right)$ $ Leftrightarrow tan left( {x + frac{pi }{4}} right) = m.$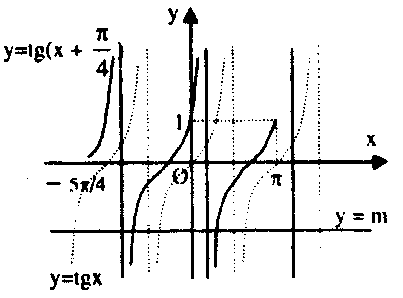 Ta có kết luận:
Ta có kết luận:
+ Với $m ge 1$ hoặc $m le 0$, phương trình có hai nghiệm phân biệt thuộc $D.$
+ Với $0 < m < 1$, phương trình có ba nghiệm phân biệt thuộc $D.$II. CÁC BÀI TOÁN THI
Bài 1: (ĐHSP II – 2000): Tìm các nghiệm nguyên của phương trình:
$cos left[ {frac{pi }{8}left( {3x – sqrt {9{x^2} + 160x + 800} } right)} right] = 1.$Biến đổi tương đương phương trình về dạng:
$frac{pi }{8}left( {3x – sqrt {9{x^2} + 160x + 800} } right) = 2kpi $ $ Leftrightarrow sqrt {9{x^2} + 160x + 800} = 3x – 16k$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{3x – 16k ge 0}\
{9{x^2} + 160x + 800 = {{(3x – 16k)}^2}}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{x ge frac{{16k}}{3},k in Z}\
{(3k + 5)x = 8{k^2} – 25}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{frac{{8{k^2} – 25}}{{3k + 5}} ge frac{{16k}}{3},k in Z}\
{x = frac{{8{k^2} – 25}}{{3k + 5}}}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{k < – frac{5}{3},k in Z:left( 1 right)}\
{9x = 24k – 40 – frac{{25}}{{3k + 5}}:left( 2 right)}
end{array}} right..$
Muốn $x$ nguyên thì trước hết từ $(2)$ ta phải có:
$frac{{25}}{{3k + 5}} in Z$ $ Leftrightarrow 3k + 5$ là ước của $25$ $mathop Leftrightarrow limits^{left( 1 right)} left[ {begin{array}{*{20}{l}}
{3k + 5 = – 1}\
{3k + 5 = – 5}\
{3k + 5 = – 25}
end{array}} right.$ $mathop Leftrightarrow limits^{k in Z} left[ {begin{array}{*{20}{l}}
{k = – 2}\
{k = – 10}
end{array}} right..$
+ Với $k = – 2$, ta được $x= – 7.$
+ Với $k = -10$, ta được $x = -31.$
Vậy phương trình có hai nghiệm nguyên $x = -7$ và $x = – 31.$ Bài 2: (Đại học tổng hợp Lômônốp – 1982): Giải phương trình:
$sqrt { – {x^8} + 3{x^4} – 2} .sin left[ {pi left( {16{x^2} + 2x} right] = 0} right..$Biến đổi tương đương phương trình về dạng:
$left[ {begin{array}{*{20}{l}}
{ – {x^8} + 3{x^4} – 2 = 0:left( 1 right)}\
{left{ {begin{array}{*{20}{l}}
{ – {x^8} + 3{x^4} – 2 > 0:left( 2 right)}\
{sin left[ {pi left( {16{x^2} + 2x} right)} right] = 0:left( 3 right)}
end{array}} right.}
end{array}} right.$
Giải $(1)$ bằng cách đặt $t = {x^4}$, điều kiện $t ge 0$, ta được:
$(1) Leftrightarrow {t^2} – 3t + 2 = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{t = 1}\
{t = 2}
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{{x^4} = 1}\
{{x^4} = 2}
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = pm 1}\
{x = pm sqrt[4]{2}}
end{array}} right..$
Giải $(2)$, dựa vào lời giải của $(1)$ ta được:
$(2) Leftrightarrow 1 < t < 2$ $ Leftrightarrow 1 < {x^4} < 2$ $ Leftrightarrow 1 < |x| < sqrt[4]{2}$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{ – sqrt[4]{2} < x < – 1}\
{1 < x < sqrt[4]{2}}
end{array}} right..$
Giải $(3)$, ta có:
$(3) Leftrightarrow pi left( {16{x^2} + 2x} right) = kpi $ $ Leftrightarrow 16{x^2} + 2x – k = 0$ $(4).$
Phương trình $(4)$ có nghiệm khi:
$Delta’ ge 0$ $ Leftrightarrow 1 + 16k ge 0$ $ Leftrightarrow k ge – frac{1}{{16}}$ $mathop Leftrightarrow limits^{k in Z} k ge 0.$
Khi đó $(4)$ có nghiệm: ${x_{1,2}} = frac{{ – 1 pm sqrt {1 + 16k} }}{{16}}.$
Để nghiệm ${x_1} = frac{{ – 1 + sqrt {1 + 16k} }}{{16}}$ $( ge 0)$ thoả mãn $(2)$ điều kiện là:
$1 < frac{{ – 1 + sqrt {1 + 16k} }}{{16}} < sqrt[4]{2}$ $ Leftrightarrow 17 < sqrt {1 + 16k} < 1 + 16sqrt[4]{2}$ $ Leftrightarrow 18 < k < 16sqrt 2 + 2sqrt[4]{2}$ $mathop Leftrightarrow limits^{k in Z} k = { 19,20,21,22,23,24,25} .$
Để nghiệm ${x_2} = frac{{ – 1 – sqrt {1 + 16k} }}{{16}}$ $(<0)$ thoả mãn $(2)$ điều kiện là:
$ – sqrt[4]{2} < frac{{ – 1 – sqrt {1 + 16k} }}{{16}} < – 1$ $ Leftrightarrow 15 < sqrt {1 + 16k} < 16sqrt[4]{2} – 1$ $ Leftrightarrow 14 < k < 16sqrt 2 – 2sqrt[4]{2}$ $mathop Leftrightarrow limits^{k in Z} k = { 15,16,17,18,19,20} .$
Vậy phương trình có các nghiệm:
$x = left{ { pm 1, pm sqrt[4]{2}} right}$ $ cup left{ {x = frac{{ – 1 + sqrt {1 + 16k} }}{{16}}|k = overline {19,25} } right}$ $ cup left{ {x = frac{{ – 1 – sqrt {1 + 16k} }}{{16}}|k = overline {15,20} } right}.$Bài 3: Giải và biện luận phương trình: $frac{{{a^2}}}{{1 – {{tan }^2}x}} = frac{{{{sin }^2}x + {a^2} – 2}}{{cos 2x}}.$Điều kiện:
$left{ {begin{array}{*{20}{l}}
{cos x ne 0}\
{1 – {{tan }^2}x ne 0}\
{cos 2x ne 0}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{cos x ne 0}\
{1 – {{tan }^2}x ne 0}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{cos x ne 0}\
{tan x ne pm 1}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{x ne frac{pi }{2} + kpi }\
{x ne pm frac{pi }{4} + kpi }
end{array}} right.$, $k in Z.$
Biến đổi phương trình về dạng:
$frac{{{a^2}}}{{1 – {{tan }^2}x}} = frac{{{{sin }^2}x + {a^2} – 2}}{{{{cos }^2}x – {{sin }^2}x}}$ $ Leftrightarrow frac{{{a^2}}}{{1 – {{tan }^2}x}} = frac{{{{tan }^2}x + left( {{a^2} – 2} right)left( {1 + {{tan }^2}x} right)}}{{1 – {{tan }^2}x}}$ $ Leftrightarrow left( {{a^2} – 1} right){tan ^2}x = 2$ $(1).$
Với ${a^2} – 1 = 0 Leftrightarrow a = pm 1$, khi đó $(1)$ vô nghiệm.
Với ${a^2} – 1 ne 0 Leftrightarrow a ne pm 1$, khi đó $(1)$ có dạng:
${tan ^2}x = frac{2}{{{a^2} – 1}}$ $(2).$
Để $(2)$ có nghiệm và thoả mãn điều kiện ta cần có:
$left{ {begin{array}{*{20}{l}}
{frac{2}{{{a^2} – 1}} ge 0}\
{frac{2}{{{a^2} – 1}} ne 1}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{|a| > 1}\
{a ne pm sqrt 3 }
end{array}} right..$
Khi đó: $(2) Leftrightarrow tan x = pm tan alpha $ $ Leftrightarrow x = pm alpha + kpi $, $k in Z.$
Kết luận:
+ Với $|a| le 1$ hoặc $a = pm sqrt 3 $, phương trình vô nghiệm.
+ Với $a in ( – infty , – 1) cup (1, + infty )backslash left{ { pm sqrt 3 } right}$, phương trình có hai họ nghiệm.III. BÀI TẬP ĐỀ NGHỊ
Bài tập 1: Giải các phương trình sau:
a. $sin (pi cos 2x) = 1.$
b. $cos (pi cos 3x) = 1.$Bài tập 2: Giải các phương trình sau:
a. $cos (pi sin x) = 1.$
b. $sin frac{pi }{x} = cos (pi x).$
c. $cos left[ {frac{pi }{2}cos left( {x – frac{pi }{4}} right)} right] = frac{1}{2}.$Bài tập 3: Giải các phương trình sau:
a. $tan left[ {frac{pi }{4}(cos x – sin x)} right] = 1.$
b. $cot left[ {frac{pi }{4}(cos x + sin x)} right] = 1.$Bài tập 4: Giải và biện luận các phương trình sau:
a. $cos (x + alpha ) + cos (x – alpha ) = 2cos alpha .$
b. $sin (x + alpha ) + cos (x – alpha ) = 1 + sin alpha .$
c. $(m + 1)sin 2x + 1 – {m^2} = 0.$
d. $(m + 2)tan 2x – sqrt m = 0.$Bài tập 5: Biện luận theo $m$ số nghiệm của phương trình:
a. $sin x = m$ với $x in left( { – frac{pi }{4},frac{{4pi }}{3}} right].$
b. $sin left( {2x – frac{pi }{4}} right) = m$ với $x in left[ { – frac{pi }{{24}},frac{{19pi }}{8}} right].$
c. $cos left( {x – frac{pi }{3}} right) = m$ với $x in left[ {frac{{5pi }}{6},frac{{13pi }}{6}} right].$
d. $cot left( {x – frac{pi }{4}} right) = m$ với $x in left( { – frac{{5pi }}{4},pi } right).$

Be the first to comment