
Tài liệu hướng dẫn phương pháp tính góc giữa hai mặt phẳng cắt nhau trong không gian, đây là một nội dung rất quan trọng trong chương trình Hình học 11 chương 3. Kiến thức và các ví dụ minh họa trong bài viết được tham khảo từ các tài liệu hình học không gian được chia sẻ trên TOANPDF.com.Bài toán: Cho hai mặt phẳng $(α)$ và $(β)$ cắt nhau, tính góc giữa hai mặt phẳng $(α)$ và $(β).$Ta áp dụng một trong các phương pháp sau đây:Phương pháp 1
Dựng hai đường thẳng $a$, $b$ lần lượt vuông góc với hai mặt phẳng $left( alpha right)$ và $left( beta right)$. Khi đó, góc giữa hai mặt phẳng $left( alpha right)$ và $left( beta right)$ là $left( {widehat {left( alpha right),left( beta right)}} right) = left( {widehat {a,b}} right).$ Tính góc $left( {widehat {a,b}} right).$Phương pháp 2
+ Xác định giao tuyến $c$ của hai mặt phẳng $left( alpha right)$ và $left( beta right).$
+ Dựng hai đường thẳng $a$, $b$ lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến $c$ tại một điểm trên $c.$ Khi đó: $left( {widehat {left( alpha right),left( beta right)}} right) = left( {widehat {a,b}} right).$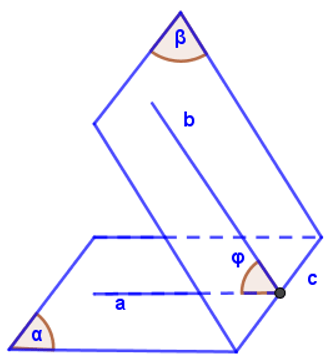 Hiểu cách khác: Ta xác định mặt phẳng phụ $left( gamma right)$ vuông góc với giao tuyến $c$ mà $left( alpha right) cap left( gamma right) = a$, $left( beta right) cap left( gamma right) = b.$ Suy ra $left( {widehat {left( alpha right),left( beta right)}} right) = left( {widehat {a,b}} right).$Phương pháp 3 (trường hợp đặc biệt)
Hiểu cách khác: Ta xác định mặt phẳng phụ $left( gamma right)$ vuông góc với giao tuyến $c$ mà $left( alpha right) cap left( gamma right) = a$, $left( beta right) cap left( gamma right) = b.$ Suy ra $left( {widehat {left( alpha right),left( beta right)}} right) = left( {widehat {a,b}} right).$Phương pháp 3 (trường hợp đặc biệt) Nếu có một đoạn thẳng nối hai điểm $A$, $B$ $left( {A in left( alpha right), B in left( beta right)} right)$ mà $AB bot left( beta right)$ thì qua $A$ hoặc $B$ ta dựng đường thẳng vuông góc với giao tuyến $c$ của hai mặt phẳng tại $H.$ Khi đó $left( {widehat {left( alpha right),left( beta right)}} right) = widehat {AHB}.$Ví dụ 1. Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy $ABCD$ bằng $a$ và $SA = SB = SC = SD = a.$ Tính $cosin$ góc giữa hai mặt phẳng $left( {SAB} right)$ và $left( {SAD} right).$
Nếu có một đoạn thẳng nối hai điểm $A$, $B$ $left( {A in left( alpha right), B in left( beta right)} right)$ mà $AB bot left( beta right)$ thì qua $A$ hoặc $B$ ta dựng đường thẳng vuông góc với giao tuyến $c$ của hai mặt phẳng tại $H.$ Khi đó $left( {widehat {left( alpha right),left( beta right)}} right) = widehat {AHB}.$Ví dụ 1. Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy $ABCD$ bằng $a$ và $SA = SB = SC = SD = a.$ Tính $cosin$ góc giữa hai mặt phẳng $left( {SAB} right)$ và $left( {SAD} right).$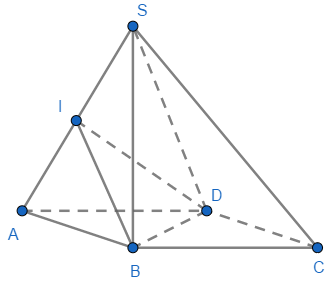 Gọi $I$ là trung điểm $SA.$ Do tam giác $SAD$ và $SAB$ đều nên:
Gọi $I$ là trung điểm $SA.$ Do tam giác $SAD$ và $SAB$ đều nên:
$left{ begin{array}{l}
BI bot SA\
DI bot SA
end{array} right.$ $ Rightarrow left( {widehat {left( {SAB} right),left( {SAD} right)}} right) = left( {widehat {BI,DI}} right).$
Áp dụng định lý $cosin$ cho tam giác $BID$ ta có:
$cos widehat {BID} = frac{{I{B^2} + I{D^2} – B{D^2}}}{{2IB.ID}}$ $ = frac{{{{left( {frac{{sqrt 3 }}{2}a} right)}^2} + {{left( {frac{{sqrt 3 }}{2}a} right)}^2} – {{left( {asqrt 2 } right)}^2}}}{{2.frac{{sqrt 3 }}{2}a.frac{{sqrt 3 }}{2}a}}$ $ = – frac{1}{3}.$
Vậy $cos left( {widehat {left( {SAB} right),left( {SAD} right)}} right) = frac{1}{3}.$Ví dụ 2. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là nửa lục giác đều nội tiếp đường tròn đường kính $AB = 2a$, $SA$ vuông góc với $left( {ABCD} right)$ và $SA = asqrt 3 .$ Tính góc giữa hai mặt phẳng $left( {SBC} right)$ và $left( {SCD} right).$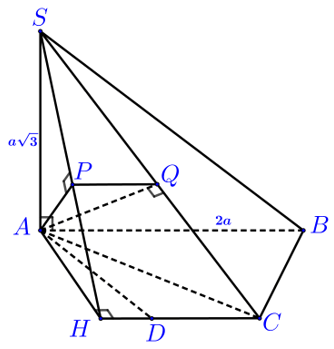 Vì $ABCD$ là nửa lục giác đều nên $AD = DC = CB = a.$
Vì $ABCD$ là nửa lục giác đều nên $AD = DC = CB = a.$
Dựng đường thẳng đi qua $A$ và vuông góc với $left( {SCD} right).$
Trong mặt phẳng $left( {ABCD} right)$ dựng $AH bot CD$ tại $H$ $ Rightarrow CD bot left( {SAH} right).$
Trong mặt phẳng $left( {SAH} right)$ dựng $AP bot SH$ $ Rightarrow CD bot AP$ $ Rightarrow AP bot left( {SCD} right).$
Dựng đường thẳng đi qua $A$ và vuông góc với $left( {SBC} right).$
Trong mặt phẳng $left( {SAC} right)$ dựng $AQ bot SC.$
Lại có $AQ bot BC$ vì $left{ begin{array}{l}
BC bot AC\
BC bot SA
end{array} right.$ $ Rightarrow BC bot left( {SAC} right)$ $ Rightarrow BC bot AQ.$
Vậy $AQ bot left( {SBC} right).$Suy ra góc giữa hai mặt phẳng $left( {SBC} right)$ và $left( {SCD} right)$ là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng ấy là $AP$ và $AQ.$
Ta tính góc $widehat {PAQ}$, có $AH = sqrt {A{D^2} – H{D^2}} $ $ = sqrt {{a^2} – frac{{{a^2}}}{4}} = frac{{asqrt 3 }}{2}.$
$ Rightarrow frac{1}{{A{P^2}}} = frac{1}{{A{S^2}}} + frac{1}{{A{H^2}}}$ $ Rightarrow AP = frac{{asqrt 3 }}{{sqrt 5 }}.$
Tam giác $SAC$ vuông cân tại $A$ $ Rightarrow AQ = frac{{SC}}{2} = frac{{asqrt 6 }}{2}.$
$Delta APQ$ vuông tại $P$ $ Rightarrow cos widehat {PAQ} = frac{{AP}}{{AQ}} = frac{{sqrt {10} }}{5}$ $ Rightarrow widehat {PAQ}$ $ = arccos frac{{sqrt {10} }}{5}.$Ví dụ 3. Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân với $BA = BC = a$, $SA bot left( {ABC} right)$, $SA = a.$ Gọi $E, F$ lần lượt là trung điểm của các cạnh $AB, AC.$ Tính $cosin$ góc giữa hai mặt phẳng $left( {SEF} right)$ và $left( {SBC} right).$
Nhận xét: Giao tuyến của hai mặt phẳng $left( {SEF} right)$ và $left( {SBC} right)$ là đường thẳng $St$ đi qua $S$ và song song với $EF$ và $BC$ nên ta xác định hai đường thẳng qua $S$ và lần lượt nằm trong hai mặt phẳng $left( {SEF} right)$ và $left( {SBC} right)$ và cùng vuông góc với $St$ (ta đi chứng minh hai đường thẳng đó là $SE$ và $SB$).Vì $left{ begin{array}{l}
EF subset left( {SEF} right)\
BC subset left( {SBC} right)\
EF {rm{//}} BC
end{array} right. $ $⇒$ giao tuyến của $left( {SEF} right)$ và $left( {SBC} right)$ là đường thẳng qua $S$, song song với $BC$, là $St.$Ta có $left{ begin{array}{l}
BC bot AB\
BC bot SAleft( {vì SA bot left( {ABC} right)} right)
end{array} right. $ $ Rightarrow BC bot left( {SAB} right)$ $ Rightarrow BC bot SB$ hay $St bot SB.$
Tương tự $EF bot left( {SAE} right)$ $ Rightarrow EF bot SE$ mà $EF {rm{//}} St$ $ Rightarrow St bot SE.$
Vậy $SB$ và $SE$ cùng đi qua $S$ và cùng vuông góc với $St$ nên góc giữa hai mặt phẳng $left( {SEF} right)$ và $left( {SBC} right)$ bằng góc giữa hai đường thẳng $SB$ và $SE.$
Ta tính góc $widehat {BSE}.$
Có $SE = sqrt {S{A^2} + A{E^2}} = frac{{asqrt 5 }}{2}$; $SB = sqrt {S{A^2} + A{B^2}} = asqrt 2 $; $BE = frac{a}{2}.$
Theo định lí $cosin$ ta có: $cos widehat {BSE} = frac{{S{E^2} + S{B^2} – B{E^2}}}{{2.SE.SB}}$ $ = frac{3}{{sqrt {10} }}$ $ Rightarrow widehat {BSE} = arccos frac{3}{{sqrt {10} }}.$Ví dụ 4. Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $B$, $SA = a$ và $SA bot left( {ABC} right)$, $AB = BC = a.$ Tính góc giữa hai mặt phẳng $left( {SAC} right)$ và $left( {SBC} right).$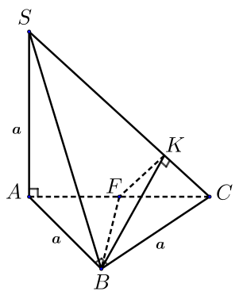
Nhận xét: Ta áp dụng phương pháp 3 (trường hợp đặc biệt).Ta có $left( {SAC} right) cap left( {SBC} right) = SC.$
Gọi $F$ là trung điểm $AC$ $ Rightarrow BF bot left( {SAC} right).$
Dựng $BK bot SC$ tại $K$ $ Rightarrow SC bot left( {BKF} right)$ $ Rightarrow widehat {left( {left( {SAC} right),left( {SBC} right)} right)}$ $ = widehat {left( {KB,KF} right)} = widehat {BKF}.$
$Delta CFK sim Delta CSA Rightarrow frac{{FK}}{{FC}} = frac{{SA}}{{SC}}$ $ Rightarrow FK = frac{{FC.SA}}{{SC}}$ $ = frac{{frac{{asqrt 2 }}{2}.a}}{{asqrt 3 }} = frac{a}{{sqrt 6 }}.$
$Delta BFK$ vuông tại $F$ $ Rightarrow tan widehat {BKF} = frac{{FB}}{{FK}}$ $ = frac{{frac{{asqrt 2 }}{2}}}{{frac{a}{{sqrt 6 }}}} = sqrt 3 $ $ Rightarrow widehat {BKF} = 60^circ $ $ = widehat {left( {left( {SAC} right),left( {SBC} right)} right)}.$Ví dụ 5. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là nửa lục giác đều nội tiếp đường tròn đường kính $AB = 2a$, $SA$ vuông góc với $left( {ABCD} right)$ và $SA = asqrt 3 .$ Tính $tan$ của góc giữa hai mặt phẳng $left( {SAD} right)$ và $left( {SBC} right).$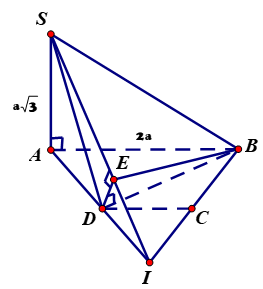
Gọi $I = AD cap BC$, $ABCD$ là nửa lục giác đều nên $AD = DC = CB = a$, $AI = IB = a.$
$left( {SAD} right) cap left( {SBC} right) = SI$ $ Rightarrow left{ begin{array}{l}
BD bot SA\
BD bot AD
end{array} right.$ $ Rightarrow BD bot left( {SAD} right) Rightarrow BD bot SI.$
Vì vậy theo trường hợp đặc biệt ta chỉ cần dựng $DE bot SI$ với $E in SI.$
Khi đó, $SI bot left( {BED} right)$ $ Rightarrow left( {widehat {left( {SAD} right),left( {SSBC} right)}} right) = left( {widehat {EB,ED}} right)$ $ = widehat {BED}$ (Vì $Delta BED$ vuông tại $D$).
$Delta AIB$ đều nên $BD = asqrt 3 .$
$SI = sqrt {S{A^2} + A{I^2}} = asqrt 7 .$
Hai tam giác vuông $SAI$ và $DEI$ đồng dạng nên: $frac{{DE}}{{SA}} = frac{{DI}}{{SI}} Rightarrow DE = frac{{asqrt 3 }}{{sqrt 7 }}.$
$Delta BDE$ vuông tại $D$ $ Rightarrow tan widehat {BED} = frac{{BD}}{{DE}} = sqrt 7 .$Ví dụ 6. Cho tam giác $ABC$ vuông cân tại $A$ có $AB = a$, trên đường thẳng $d$ vuông góc với $left( {ABC} right)$ tại điểm $A$ ta lấy một điểm $D.$ Tính góc giữa hai mặt phẳng $left( {ABC} right)$ và $left( {DBC} right)$, trong trường hợp $left( {DBC} right)$ là tam giác đều.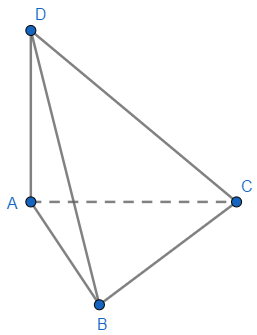
Gọi $varphi $ là góc giữa hai mặt phẳng $left( {ABC} right)$ và $left( {DBC} right).$
Theo công thức diện tích hình chiếu của đa giác, ta có: ${S_{Delta ABC}} = {S_{Delta DBC}}.cosvarphi .$
Mà: ${S_{ΔDBC}} = frac{1}{2}DB.DC.sin {60^0}$ $ = frac{1}{2}asqrt 2 .asqrt 2 .frac{{sqrt 3 }}{2} = frac{{{a^2}sqrt 3 }}{2}.$
Mặt khác: ${S_{ΔABC}} = frac{1}{2}AB.AC = frac{1}{2}{a^2}.$
$ Rightarrow cos varphi = frac{{{S_{ΔABC}}}}{{{S_{ΔDBC}}}} = frac{{sqrt 3 }}{3}$ $ Rightarrow varphi = arccos frac{{sqrt 3 }}{3}.$Ví dụ 7. Cho lăng trụ đứng $OAB.O’A’B’$ có các đáy là các tam giác vuông cân $OA = OB = a, AA’ = asqrt 2 .$ Gọi $M, P$ lần lượt là trung điểm các cạnh $OA, AA’.$ Tính diện tích thiết diện khi cắt lăng trụ bởi $left( {B’MP} right).$
Gọi $R$ là giao điểm của $MP$ và $OO’$, $Q$ là giao điểm của $B’R$ với $OB.$
Thiết diện là tứ giác $MPB’Q$, ta có: $frac{{OQ}}{{O’B’}} = frac{{RO}}{{RO’}} = frac{1}{3}$ $ Rightarrow OQ = frac{a}{3}.$
Tứ giác $AMQB$ là hình chiếu vuông góc của tứ giác $PMQB’$ trên mặt phẳng $left( {OAB} right)$ nên: ${S_{PMQB’}} = frac{{{S_{AMQB}}}}{{cos varphi }}.$
Với $varphi $ là góc tạo bởi hai mặt phẳng $left( {OAB} right)$ và $left( {MPB’Q} right).$
Ta có: ${S_{AMQB}} = {S_{OAB}} – {S_{OMQ}}$ $ = frac{1}{2}{a^2} – frac{1}{{12}}{a^2} = frac{5}{{12}}{a^2}.$
Hạ $OH bot MQ$, ta có: $left{ begin{array}{l}
MQ bot OH\
MQ bot OR
end{array} right. Rightarrow MQ bot left( {OHR} right).$
Vậy: $varphi = widehat {OHR}$ ($widehat {OHR}$ nhọn).
Ta có: $cos varphi = coswidehat {OHR} = frac{{OH}}{{RH}}$ $ = frac{{OH}}{{sqrt {O{H^2} + O{R^2}} }}$ $ = frac{{frac{a}{{sqrt {13} }}}}{{sqrt {frac{{{a^2}}}{{13}} + frac{{{a^2}}}{2}} }} = frac{{sqrt 2 }}{{sqrt {15} }}.$
Vậy: ${S_{PMQB’}} = frac{{5{a^2}sqrt {15} }}{{12sqrt 2 }}.$Ví dụ 8. Cho lăng trụ đứng $ABC.A’B’C’$ có đáy $ABC$ là một tam giác cân với $AB = AC = a,widehat {BAC} = {120^0},$ cạnh bên $BB’ = a.$ Gọi $I$ là trung điểm $CC’.$ Chứng minh rằng tam giác $AB’I$ vuông ở $A$. Tính $cosin$ của góc giữa hai mặt phẳng $left( {ABC} right)$ và $left( {AB’I} right).$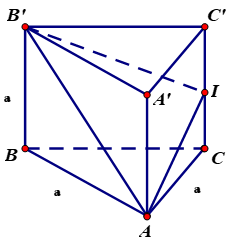
Áp dụng định lý $cosin$ cho $Delta ABC$ ta có: $B{C^2} = {a^2} + {a^2} – 2{a^2}{rm{cos}}{120^0}$ $ = 3{a^2}.$
Áp dụng định lý Py-ta-go cho các tam giác:
$Delta B’BA$: $B'{A^2} = 2{a^2}.$
$Delta ICA$: $A{I^2} = {a^2} + {left( {frac{1}{2}} right)^2} = frac{{5{a^2}}}{4}.$
$Delta B’C’I$: $B'{I^2} = 3{a^2} + frac{{{a^2}}}{4} = frac{{13{a^2}}}{4}.$
Ta có: $B'{A^2} + A{I^2} = 2{a^2} + frac{{5{a^2}}}{4}$ $ = frac{{13{a^2}}}{4} = B'{I^2} Rightarrow Delta AB’I$ vuông ở $A.$
Ta có: ${S_{Delta AB’I}} = frac{1}{2}AI.AB’$ $ = frac{1}{2}.frac{{asqrt 5 }}{2}.asqrt 2 = frac{{{a^2}sqrt {10} }}{4}.$
${S_{Delta ABC}} = frac{1}{2}{a^2}sin {120^0} = frac{{{a^2}sqrt 3 }}{4}.$
Gọi $varphi $ là góc giữa hai mặt phẳng $left( {ABC} right)$ và $left( {AB’I} right).$ Khi đó:
$cosvarphi = frac{{{S_{Delta ABC}}}}{{{S_{Delta ABI’}}}}$ $ = frac{{frac{{{a^2}sqrt 3 }}{4}}}{{frac{{{a^2}sqrt {10} }}{4}}} = frac{{sqrt 3 }}{{sqrt {10} }} = frac{{sqrt {30} }}{{10}}.$

Be the first to comment