
Bài viết hướng dẫn phương pháp giải một số dạng toán thường gặp liên quan đến bất phương trình bậc hai trong chương trình Đại số 10 chương 4.A. LÝ THUYẾT CẦN NẮM VỮNG
1. Định nghĩa và cách giải bất phương trình bậc hai
+ Bất phương trình bậc hai (ẩn $x$) là bất phương trình có một trong các dạng $fleft( x right)>0$, $f(x)<0$, $f(x)ge 0$, $f(x)le 0$ trong đó $f(x)$ là một tam thức bậc hai.
+ Để giải bất phương trình bậc hai, ta áp dụng định lí về .
2. Ứng dụng giải toán: Giải bất phương trình tích, thương chứa các tam thức bậc hai bằng cách lập bảng xét dấu.B. CÁC DẠNG TOÁN BẤT PHƯƠNG TRÌNH BẬC HAI
Dạng toán 1. Giải bất phương trình bậc hai.
Ví dụ 1. Giải các bất phương trình sau:
a) $-3{{x}^{2}}+2x+1<0.$
b) ${{x}^{2}}+x-12<0.$
c) $5{{x}^{2}}-6sqrt{5}x+9>0.$
d) $-36{{x}^{2}}+12x-1ge 0.$a) Tam thức $f(x)=-3{{x}^{2}}+2x+1$ có $a=-3<0$ và có hai nghiệm ${{x}_{1}}=-frac{1}{3}$, ${{x}_{2}}=1.$
($f(x)$ cùng dấu với hệ số $a$).
Suy ra $-3{{x}^{2}}+2x+1<0$ $Leftrightarrow x<-frac{1}{3}$ hoặc $x>1.$
Vậy tập nghiệm của bất phương trình: $S=(-infty ;-frac{1}{3})cup (1;+infty ).$
b) Tam thức $fleft( x right)={{x}^{2}}+x-12$ có $a=1>0$ và có hai nghiệm ${{x}_{1}}=-4$, ${{x}_{2}}=3.$
($f(x)$ trái dấu với hệ số $a$).
Suy ra ${{x}^{2}}+x-12<0$ $Leftrightarrow -4<x<3.$
Vậy tập nghiệm của bất phương trình là $text{S}=left( -4;3 right).$
c) Tam thức $fleft( x right)=5{{x}^{2}}-6sqrt{5}x+9$ có $a=5>0$ và $Delta =0.$
($f(x)$ cùng dấu với hệ số $a$).
Suy ra $5{{x}^{2}}-6sqrt{5}x+9>0$ $Leftrightarrow xne frac{3sqrt{5}}{5}.$
Vậy tập nghiệm của bất phương trình là $text{S}=mathbb{R}backslash left{ frac{3sqrt{5}}{5} right}.$
d) Tam thức $fleft( x right)=-36{{x}^{2}}+12x-1$ có $a=-36<0$ và $Delta =0.$
$fleft( x right)$ âm với $forall xne frac{1}{6}$ và $fleft( frac{1}{6} right)=0.$
Suy ra $-36{{x}^{2}}+12x-1ge 0$ $Leftrightarrow x=frac{1}{6}.$
Vậy tập nghiệm của bất phương trình là $text{S}=left{ frac{1}{6} right}.$Ví dụ 2. Tìm $m$ để phương trình sau có nghiệm:
a) ${{x}^{2}}-mx+m+3=0.$
b) $(1+m){{x}^{2}}-2mx+2m=0.$a) Phương trình có nghiệm khi và chỉ khi $Delta ge 0$ $Leftrightarrow {{m}^{2}}-4left( m+3 right)ge 0$ $Leftrightarrow {{m}^{2}}-4m-12ge 0$ $Leftrightarrow left[ begin{matrix}
mge 6 \
mle -2 \
end{matrix} right.$
Vậy với $min (-infty ;-2]cup [6;+infty )$ thì phương trình có nghiệm.
b)
+ Với $m=-1$ phương trình trở thành $2x-2=0$ $Leftrightarrow x=1$ suy ra $m=-1$ thỏa mãn yêu cầu bài toán.
+ Với $mne -1$ phương trình có nghiệm khi và chỉ khi $Delta’ ge 0$ $Leftrightarrow {{m}^{2}}-2mleft( 1+m right)ge 0$ $Leftrightarrow {{m}^{2}}+2mle 0$ $Leftrightarrow -2le mle 0.$
Vậy với $-2le mle 0$ thì phương trình có nghiệm.Ví dụ 3. Tìm $m$ để mọi $xin left[ -1;1 right]$ đều là nghiệm của bất phương trình $3{{x}^{2}}-2left( m+5 right)x-{{m}^{2}}+2m+8le 0.$Ta có $3{{x}^{2}}-2left( m+5 right)x-{{m}^{2}}+2m+8=0$ $Leftrightarrow x=m+2$ hoặc $x=frac{4-m}{3}.$
+ Với $m+2>frac{4-m}{3}$ $Leftrightarrow 3m+6>4-m$ $Leftrightarrow m>-frac{1}{2}$, ta có:
Bất phương trình $Leftrightarrow frac{4-m}{3}le xle m+2.$
Vậy tập nghiệm của bất phương trình là $left[ frac{4-m}{3};m+2 right].$
Suy ra mọi $xin left[ -1;1 right]$ đều là nghiệm của bất phương trình khi và chỉ khi $left[ -1;1 right]subset left[ frac{4-m}{3};m+2 right]$ $Leftrightarrow left{ begin{matrix}
-1ge frac{4-m}{3} \
1le m+2 \
end{matrix} right.$ $Leftrightarrow left{ begin{matrix}
mge 7 \
mge -1 \
end{matrix} right.$ $Leftrightarrow mge 7.$
Kết hợp với điều kiện $m>-frac{1}{2}$ ta có $mge 7$ thỏa mãn yêu cầu bài toán.
+ Với $m+2<frac{4-m}{3}$ $Leftrightarrow m<-frac{1}{2}$, ta có:
Bất phương trình $Leftrightarrow m+2le xle frac{4-m}{3}.$
Vậy tập nghiệm của bất phương trình là $left[ m+2;frac{4-m}{3} right].$
Suy ra mọi $xin left[ -1;1 right]$ đều là nghiệm của bất phương trình khi và chỉ khi $left[ -1;1 right]subset left[ m+2;frac{4-m}{3} right]$ $Leftrightarrow left{ begin{matrix}
-1ge m+2 \
1le frac{4-m}{3} \
end{matrix} right.$ $Leftrightarrow left{ begin{matrix}
mle -3 \
mle 1 \
end{matrix} right.$ $Leftrightarrow mle -3.$
Kết hợp với điều kiện $m<-frac{1}{2}$ ta có $mle -3$ thỏa mãn yêu cầu bài toán.
+ Với $m=-frac{1}{2}$ ta có bất phương trình $Leftrightarrow x=frac{3}{2}$ nên $m=-frac{1}{2}$ không thỏa mãn yêu cầu bài toán.
Vậy $min (-infty ;-3]cup [7;+infty )$ là giá trị cần tìm.Ví dụ 4. Giải và biện luận bất phương trình $(m+1){{x}^{2}}-2(2m-1)x-4m+2<0.$Với $m=-1$, bất phương trình trở thành $6x+6<0$ $Leftrightarrow x<-1.$
Với $mne -1$ ta có $g(x)=(m+1){{x}^{2}}-2(2m-1)x-4m+2$ là tam thức bậc hai có: $a=m+1$ $Delta’=8{{m}^{2}}-2m-1.$
Bảng xét dấu: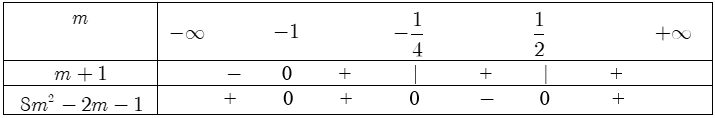 + Xét $-frac{1}{4}le mle frac{1}{2}$ $Rightarrow left{ begin{align}
+ Xét $-frac{1}{4}le mle frac{1}{2}$ $Rightarrow left{ begin{align}
& a>0 \
& Delta’le 0 \
end{align} right.$ $Rightarrow g(x)ge 0$, $forall xin R$ $Rightarrow$ bất phương trình vô nghiệm.
+ Xét $left[ begin{align}
& m>frac{1}{2} \
& -1<m<-frac{1}{4} \
end{align} right.$ $Rightarrow left{ begin{align}
& a>0 \
& Delta’>0 \
end{align} right.$ $Rightarrow $ $S=({{x}_{1}};{{x}_{2}})$, với: ${{x}_{1}}=frac{2m-1-sqrt{(2m-1)(m+1)}}{m+1}$, ${{x}_{2}}=frac{2m-1+sqrt{(2m-1)(m+1)}}{m+1}.$
+ Xét $m<-1$ $Rightarrow left{ begin{align}
& a<0 \
& Delta’>0 \
end{align} right.$ $Rightarrow $ $S=(-infty ;{{x}_{1}})cup ({{x}_{2}};+infty ).$
Kết luận:
$m=-1$ bất phương trình có tập nghiệm là $text{S}=left( -infty ;-1 right).$
$-frac{1}{4}le mle frac{1}{2}$ bất phương trình có tập nghiệm là $text{S}=varnothing .$
$left[ begin{align}
& m>frac{1}{2} \
& -1<m<-frac{1}{4} \
end{align} right.$ bất phương trình có tập nghiệm là $S=({{x}_{1}};{{x}_{2}}).$
$m<-1$ bất phương trình có tập nghiệm là $S=(-infty ;{{x}_{1}})cup ({{x}_{2}};+infty ).$Dạng toán 2. Giải hệ bất phương trình bậc hai một ẩn.
Ví dụ 5. Giải các hệ bất phương trình sau:
a) $left{ begin{align}
& 2{{x}^{2}}+9x+7>0 \
& {{x}^{2}}+x-6<0 \
end{align} right.$
b) $left{ begin{align}
& 2{{x}^{2}}+x-6>0 \
& 3{{x}^{2}}-10x+3ge 0 \
end{align} right.$
c) $left{ begin{matrix}
-{{x}^{2}}+5x-4ge 0 \
{{x}^{2}}+x-13le 0 \
end{matrix} right.$
d) $left{ begin{align}
& {{x}^{2}}+4x+3ge 0 \
& 2{{x}^{2}}-x-10le 0 \
& 2{{x}^{2}}-5x+3>0 \
end{align} right.$a) Ta có $left{ begin{align}
& 2{{x}^{2}}+9x+7>0 \
& {{x}^{2}}+x-6<0 \
end{align} right.$ $Leftrightarrow left{ begin{matrix}
left[ begin{matrix}
xge -1 \
xle -frac{7}{2} \
end{matrix} right. \
-3<x<2 \
end{matrix} right.$ $Leftrightarrow -1<x<2.$
Vậy tập nghiệm hệ bất phương trình là $S=left( -1;2 right).$
b) Ta có $left{ begin{align}
& 2{{x}^{2}}+x-6ge 0 \
& 3{{x}^{2}}-10x+3>0 \
end{align} right.$ $Leftrightarrow left{ begin{matrix}
left[ begin{matrix}
xge frac{3}{2} \
xle -2 \
end{matrix} right. \
left[ begin{matrix}
x>3 \
x<frac{1}{3} \
end{matrix} right. \
end{matrix} right.$ $Leftrightarrow left[ begin{matrix}
x>3 \
xle -2 \
end{matrix} right.$
Vậy tập nghiệm hệ bất phương trình là $S=(-infty ;-2]cup (3;+infty ).$
c) Ta có $left{ begin{matrix}
-{{x}^{2}}+5x-4ge 0 \
{{x}^{2}}+x-13le 0 \
end{matrix} right.$ $Leftrightarrow left{ begin{matrix}
1le xle 4 \
frac{-1-sqrt{53}}{2}le xle frac{-1+sqrt{53}}{2} \
end{matrix} right.$ $Leftrightarrow 1le xle frac{-1+sqrt{53}}{2}.$
Vậy tập nghiệm hệ bất phương trình là $S=left[ 1;frac{-1+sqrt{53}}{2} right].$
d) Ta có $left{ begin{align}
& {{x}^{2}}+4x+3ge 0 \
& 2{{x}^{2}}-x-10le 0 \
& 2{{x}^{2}}-5x+3le 0 \
end{align} right.$ $Leftrightarrow left{ begin{align}
& left[ begin{matrix}
xge -1 \
xle -3 \
end{matrix} right. \
& -2le xle frac{5}{2} \
& 1le xle frac{3}{2} \
end{align} right.$ $Leftrightarrow 1le xle frac{3}{2}.$
Vậy tập nghiệm hệ bất phương trình là $S=left[ 1;frac{3}{2} right].$Ví dụ 6. Cho hệ bất phương trình $left{ begin{matrix}
m{{x}^{2}}-x-5le 0 \
left( 1-m right){{x}^{2}}+2mx+m+2ge 0 \
end{matrix} right.$
a) Giải hệ bất phương trình khi $m=1.$
b) Tìm $m$ để hệ bất phương trình nghiệm đúng với mọi $x.$a) Khi $m=1$ hệ bất phương trình trở thành:
$left{ begin{matrix}
{{x}^{2}}-x-5le 0 \
2x+3ge 0 \
end{matrix} right.$ $Leftrightarrow left{ begin{matrix}
frac{1-sqrt{21}}{2}le xle frac{1+sqrt{21}}{2} \
xge -frac{3}{2} \
end{matrix} right.$ $Leftrightarrow frac{1-sqrt{21}}{2}le xle frac{1+sqrt{21}}{2}.$
Vậy tập nghiệm hệ bất phương trình là $S=left[ frac{1-sqrt{21}}{2};frac{1+sqrt{21}}{2} right].$
b)
+ Khi $m=0$ hệ bất phương trình trở thành $left{ begin{matrix}
-x-5le 0 \
{{x}^{2}}+2ge 0 \
end{matrix} right.$ do đó $m=0$ không thỏa mãn yêu cầu bài toán.
+ Khi $m=1$ theo câu a ta thấy cũng không thỏa mãn yêu cầu bài toán.
+ Khi $left{ begin{matrix}
mne 0 \
mne 1 \
end{matrix} right.$ ta có hệ bất phương trình nghiệm đúng với mọi $x$ khi và chỉ khi các bất phương trình trong hệ bất phương trình nghiệm đúng với mọi $x.$
$Leftrightarrow left{ begin{matrix}
left{ begin{matrix}
m<0 \
{{Delta }_{1}}=1+20mle 0 \
end{matrix} right. \
left{ begin{matrix}
1-m>0 \
Delta {{‘}_{2}}={{m}^{2}}-left( 1-m right)left( m+2 right)le 0 \
end{matrix} right. \
end{matrix} right.$ $Leftrightarrow left{ begin{align}
& m<0 \
& mle -frac{1}{20} \
& m<1 \
& 2{{m}^{2}}+m-2le 0 \
end{align} right.$ $Leftrightarrow left{ begin{align}
& m<0 \
& mle -frac{1}{20} \
& m<1 \
& frac{-1-sqrt{17}}{4}le mle frac{-1+sqrt{17}}{4} \
end{align} right.$ $Leftrightarrow frac{-1-sqrt{17}}{4}le mle -frac{1}{20}.$
Vậy $frac{-1-sqrt{17}}{4}le mle -frac{1}{20}$ là giá trị cần tìm.Dạng toán 3. Giải bất phương trình tích và bất phương trình chứa ẩn ở mấu thức.
Ví dụ 7. Giải các bất phương trình:
a) $left( 1-2x right)left( {{x}^{2}}-x-1 right)>0.$
b) ${{x}^{4}}-5{{x}^{2}}+2x+3le 0.$a) Bảng xét dấu: Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: ${rm{S}} = left( { – infty ;frac{{1 – sqrt 5 }}{2}} right) cup left( {frac{1}{2};frac{{1 + sqrt 5 }}{2}} right).$
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: ${rm{S}} = left( { – infty ;frac{{1 – sqrt 5 }}{2}} right) cup left( {frac{1}{2};frac{{1 + sqrt 5 }}{2}} right).$
b) Bất phương trình tương đương $({{x}^{4}}-4{{x}^{2}}+4)-({{x}^{2}}-2x+1)le 0$ $Leftrightarrow {{({{x}^{2}}-2)}^{2}}-{{(x-1)}^{2}}le 0$ $Leftrightarrow ({{x}^{2}}+x-3)({{x}^{2}}-x-1)le 0.$
Bảng xét dấu: Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=left[ frac{-1-sqrt{13}}{2};frac{1-sqrt{5}}{2} right]cup left[ frac{-1+sqrt{13}}{2};frac{1+sqrt{5}}{2} right].$Ví dụ 8. Giải các bất phương trình:
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=left[ frac{-1-sqrt{13}}{2};frac{1-sqrt{5}}{2} right]cup left[ frac{-1+sqrt{13}}{2};frac{1+sqrt{5}}{2} right].$Ví dụ 8. Giải các bất phương trình:
a) $frac{{{x}^{2}}-1}{left( {{x}^{2}}-3 right)left( -3{{x}^{2}}+2x+8 right)}>0.$
b) ${{x}^{2}}+10le frac{2{{x}^{2}}+1}{{{x}^{2}}-8}.$a) Bảng xét dấu: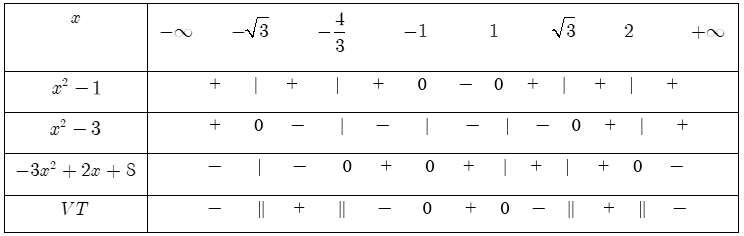 Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=left( -sqrt{3};-frac{4}{3} right)cup left( -1;1 right)cup left( sqrt{3};2 right).$
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=left( -sqrt{3};-frac{4}{3} right)cup left( -1;1 right)cup left( sqrt{3};2 right).$
b) Ta có: ${x^2} + 10 le frac{{2{x^2} + 1}}{{{x^2} – 8}}$ $ Leftrightarrow frac{{2{x^2} + 1}}{{{x^2} – 8}} – left( {{x^2} + 10} right) ge 0$ $ Leftrightarrow frac{{2{x^2} + 1 – left( {{x^2} – 8} right)left( {{x^2} + 10} right)}}{{{x^2} – 8}} ge 0$ $ Leftrightarrow frac{{81 – {x^4}}}{{{x^2} – 8}} ge 0$ $ Leftrightarrow frac{{left( {9 – {x^2}} right)left( {9 + {x^2}} right)}}{{{x^2} – 8}} ge 0$ $ Leftrightarrow frac{{9 – {x^2}}}{{{x^2} – 8}} ge 0.$
Bảng xét dấu: Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=[-3;-2sqrt{2})cup (2sqrt{2};3].$Ví dụ 9. Giải bất phương trình sau:
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=[-3;-2sqrt{2})cup (2sqrt{2};3].$Ví dụ 9. Giải bất phương trình sau:
a) $frac{left| {{x}^{2}}-x right|-2}{{{x}^{2}}-x-1}ge 0.$
b) $frac{sqrt{{{x}^{2}}+1}-sqrt{x+1}}{{{x}^{2}}+sqrt{3}x-6}le 0.$a) Vì $left| {{x}^{2}}-x right|+2>0$ nên $frac{left| {{x}^{2}}-x right|-2}{{{x}^{2}}-x-1}ge 0$ $Leftrightarrow frac{left( left| {{x}^{2}}-x right|-2 right)left( left| {{x}^{2}}-x right|+2 right)}{{{x}^{2}}-x-1}ge 0$ $Leftrightarrow frac{left( {{x}^{2}}-x-2 right)left( {{x}^{2}}-x+2 right)}{{{x}^{2}}-x-1}ge 0.$
Bảng xét dấu: Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=(-infty ;-1]cup left( frac{1-sqrt{5}}{2};frac{1+sqrt{5}}{2} right)cup [2;+infty ).$
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là: $S=(-infty ;-1]cup left( frac{1-sqrt{5}}{2};frac{1+sqrt{5}}{2} right)cup [2;+infty ).$
b) Điều kiện xác định: $left{ begin{matrix}
x+1ge 0 \
{{x}^{2}}+sqrt{3}x-6ne 0 \
end{matrix} right.$ $Leftrightarrow left{ begin{matrix}
xge -1 \
begin{align}
& xne sqrt{3} \
& xne -2sqrt{3} \
end{align} \
end{matrix} right.$ $Leftrightarrow left{ begin{matrix}
xge -1 \
xne sqrt{3} \
end{matrix} right.$
Vì $sqrt {{x^2} + 1} + sqrt {x + 1} > 0$ nên $frac{{sqrt {{x^2} + 1} – sqrt {x + 1} }}{{{x^2} + sqrt 3 x – 6}} le 0$ $ Leftrightarrow frac{{left( {sqrt {{x^2} + 1} – sqrt {x + 1} } right)left( {sqrt {{x^2} + 1} + sqrt {x + 1} } right)}}{{{x^2} + sqrt 3 x – 6}} le 0$ $ Leftrightarrow frac{{{x^2} – x}}{{{x^2} + sqrt 3 x – 6}} le 0.$
Bảng xét dấu: Dựa vào bảng xét dấu và đối chiếu điều kiện, ta có tập nghiệm của bất phương trình đã cho là: $S=left[ -1;0 right]cup [1;sqrt{3}).$Ví dụ 10. Tìm $m$ để bất phương trình $sqrt{x-{{m}^{2}}-m}left( 3-frac{x+1}{{{x}^{3}}-{{x}^{2}}-3x+3} right)<0$ có nghiệm.Ta có $sqrt{x-{{m}^{2}}-m}left( 3-frac{x+1}{{{x}^{3}}-{{x}^{2}}-3x+3} right)<0$ $Leftrightarrow left{ begin{matrix}
Dựa vào bảng xét dấu và đối chiếu điều kiện, ta có tập nghiệm của bất phương trình đã cho là: $S=left[ -1;0 right]cup [1;sqrt{3}).$Ví dụ 10. Tìm $m$ để bất phương trình $sqrt{x-{{m}^{2}}-m}left( 3-frac{x+1}{{{x}^{3}}-{{x}^{2}}-3x+3} right)<0$ có nghiệm.Ta có $sqrt{x-{{m}^{2}}-m}left( 3-frac{x+1}{{{x}^{3}}-{{x}^{2}}-3x+3} right)<0$ $Leftrightarrow left{ begin{matrix}
3-frac{x+1}{{{x}^{3}}-{{x}^{2}}-3x+3}<0 \
x>{{m}^{2}}+m \
end{matrix} right.$ $Leftrightarrow left{ begin{matrix}
frac{left( x-2 right)left( 3{{x}^{2}}+3x-4 right)}{left( x-1 right)left( {{x}^{2}}-3 right)}<0 \
x>{{m}^{2}}+m \
end{matrix} right.$
Bảng xét dấu: Tập nghiệm của bất phương trình $frac{left( x-2 right)left( 3{{x}^{2}}+3x-4 right)}{left( x-1 right)left( {{x}^{2}}-3 right)}<0$ là: $S=left( frac{-3-sqrt{57}}{6};-sqrt{3} right)cup left( frac{-3+sqrt{57}}{6};1 right)cup left( sqrt{3};2 right).$
Tập nghiệm của bất phương trình $frac{left( x-2 right)left( 3{{x}^{2}}+3x-4 right)}{left( x-1 right)left( {{x}^{2}}-3 right)}<0$ là: $S=left( frac{-3-sqrt{57}}{6};-sqrt{3} right)cup left( frac{-3+sqrt{57}}{6};1 right)cup left( sqrt{3};2 right).$
Do đó bất phương trình đã cho có nghiệm khi và chỉ khi: $Leftrightarrow {{m}^{2}}+m<2$ $Leftrightarrow {{m}^{2}}+m-2<0$ $Leftrightarrow -2<m<1.$
Vậy $-2<m<1$ là giá trị cần tìm.Dạng toán 4. Ứng dụng tam thức bậc hai, bất phương trình bậc hai trong chứng minh bất đẳng thức và tìm giá trị lớn nhất, nhỏ nhất.
Ví dụ 11. Cho hai số thực $x$, $y$. Chứng minh rằng $3{{x}^{2}}+5{{y}^{2}}-2x-2xy+1>0.$Viết bất đẳng thức lại dưới dạng $3{{x}^{2}}-2(y+1)x+5{{y}^{2}}+1>0.$
Đặt $f(x)=3{{x}^{2}}-2(y+1)x+5{{y}^{2}}+1$ và xem $y$ là tham số khi đó $fleft( x right)$ là tam thức bậc hai ẩn $x$ có hệ số ${{a}_{x}}=3>0$ và ${{Delta }_{x}}’={{(y+1)}^{2}}-3(5{{y}^{2}}+1)$ $=-14{{y}^{2}}+2y-2.$
Xét tam thức $gleft( y right)=-14{{y}^{2}}+2y-2$ có hệ số ${{a}_{y}}=-14<0$ và $Delta {{‘}_{y}}=-27<0.$
Suy ra $Delta {{‘}_{x}}<0.$
Do đó $fleft( x right)<0$ với mọi $x$, $y.$Ví dụ 12. Cho $a$, $b$, $c$ là độ dài ba cạnh của một tam giác và $x$, $y$, $z$ thỏa mãn: ${{a}^{2}}x+{{b}^{2}}y+{{c}^{2}}z=0$. Chứng minh rằng: $xy+yz+zxle 0.$+ Nếu trong ba số $x$, $y$, $z$ có một số bằng $0$, chẳng hạn $x=0$ $Rightarrow {{b}^{2}}y=-{{c}^{2}}z.$
Suy ra $xy+yz+zx=yz=-frac{{{c}^{2}}}{{{b}^{2}}}{{z}^{2}}le 0.$
+ Nếu $x,y,zne 0$. Do ${{a}^{2}}x+{{b}^{2}}y+{{c}^{2}}z=0$ $Rightarrow x=-frac{{{b}^{2}}y+{{c}^{2}}z}{{{a}^{2}}}.$
Suy ra $ xy+yz+zxle 0$ $Leftrightarrow -(y+z)frac{{{b}^{2}}y+{{c}^{2}}z}{{{a}^{2}}}+yzle 0$ $Leftrightarrow f(y)={{b}^{2}}{{y}^{2}}+({{b}^{2}}+{{c}^{2}}-{{a}^{2}})yz+{{c}^{2}}{{z}^{2}}ge 0$.
Tam thức $f(y)$ có ${{Delta }_{y}}=left[ {{({{b}^{2}}+{{c}^{2}}-{{a}^{2}})}^{2}}-4{{b}^{2}}{{c}^{2}} right]{{z}^{2}}.$
Vì $left{ begin{align}
& |b-c|<a \
& b+c>a \
end{align} right.$ $Rightarrow -2bc<{{b}^{2}}+{{c}^{2}}-{{a}^{2}}<2bc$ $Rightarrow {{({{b}^{2}}+{{c}^{2}}-{{a}^{2}})}^{2}}<4{{c}^{2}}{{b}^{2}}$ $Rightarrow {{Delta }_{y}}le 0$, $forall z$ $Rightarrow f(y)ge 0$, $forall y,z.$

Be the first to comment