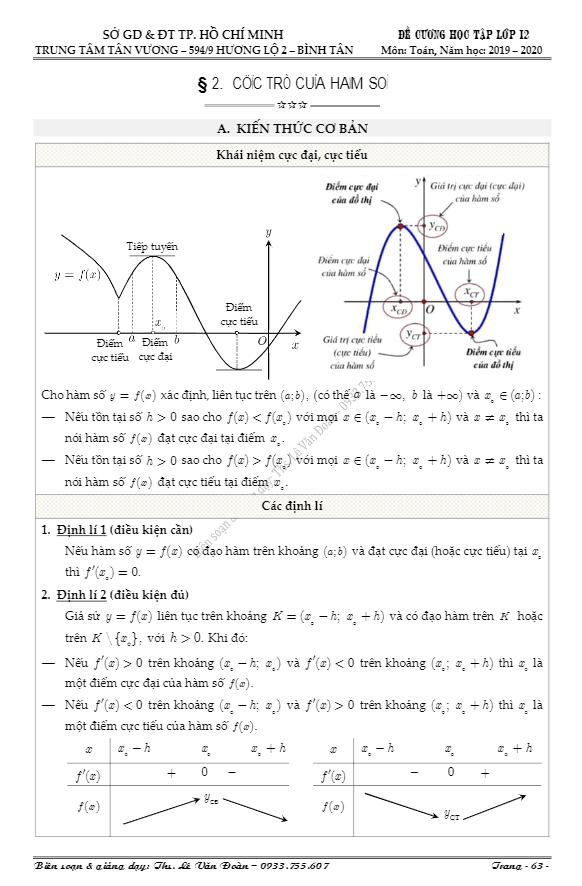
Tài liệu gồm 58 trang được biên soạn bởi thầy Lê Văn Đoàn tóm tắt lý thuyết, phân dạng, hướng dẫn giải và một số bài tập trắc nghiệm / tự luận về cực trị của hàm số, giúp học sinh tự học chương trình Giải tích 12 chương 1: .A. KIẾN THỨC CƠ BẢN
B. CÁC DẠNG TOÁN THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI
Dạng toán 1: Tìm điểm cực đại, cực tiểu, giá trị cực đại, giá trị cực tiểu.
Bài toán: Tìm các điểm cực đại, cực tiểu (nếu có) của hàm số y = f(x).
Phương pháp:
+ Bước 1. Tìm tập xác định D của hàm số.
+ Bước 2. Tính đạo hàm y’ = f'(x). Tìm các điểm xi (i = 1, 2, 3 … n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
+ Bước 3. Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
+ Bước 4. Từ bảng biến thiên, suy ra các điểm cực trị (dựa vào nội dung định lý 2).
[ads]
Dạng toán 2: Tìm tham số m để hàm số đạt cực trị tại điểm x = xo cho trước. Phương trình đường thẳng nối hai điểm cực trị.
Bài toán: Tìm tham số để hàm số y = f(x) đạt cực trị tại điểm x = x0?
Phương pháp:
+ Bước 1. Tìm tập xác định D. Tính đạo hàm y’.
+ Bước 2. Dựa vào nội dung định lí 1: Nếu hàm số y = f(x) có đạo hàm trên khoảng (a;b) và đạt cực đại (hoặc cực tiểu) tại x0 thì f'(x0) = 0.
+ Bước 3. Với m vừa tìm, thế vào hàm số và thử lại (dựa vào định lí 2 và 3).
Lưu ý:
+ Đối với hàm số bậc ba nên thử lại bằng nội dung định lý 3 (phù hợp trắc nghiệm).
+ Đối với các hàm khác chẳng hạn như bậc bốn trùng phương (thiếu b), hoặc hàm phân thức … nên thử lại bằng định lí 2.
Dạng toán 3: Biện luận hoành độ cực trị (Vận dụng & vận dụng cao).
Dạng toán 4: Cực trị của hàm hợp và hàm số trị tuyệt đối (vận dụng cao).

Be the first to comment