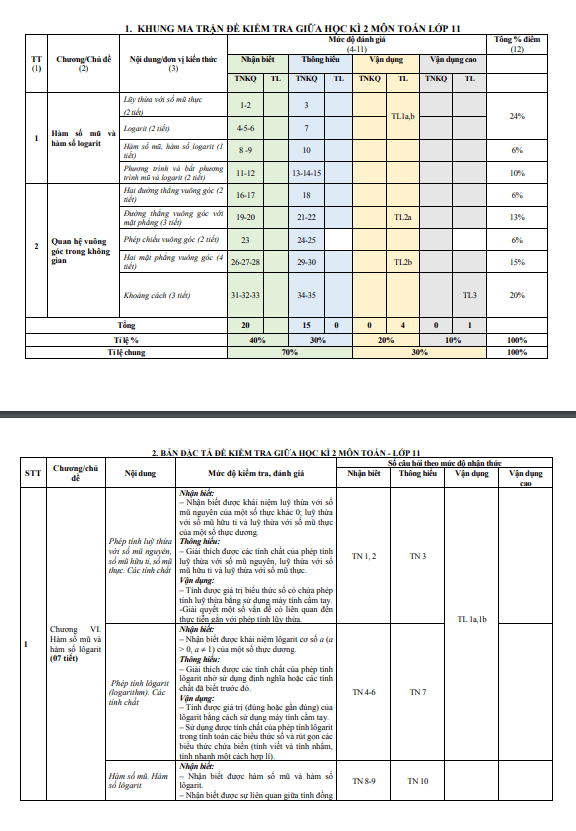
TOANPDF.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề minh họa kiểm tra giữa học kì 2 môn Toán 11 năm học 2023 – 2024 sở Giáo dục và Đào tạo tỉnh Quảng Ngãi; đề thi được biên soạn theo cấu trúc 70% trắc nghiệm + 30% tự luận (theo điểm số), có ma trận, bảng đặc tả, đáp án và hướng dẫn chấm điểm.CHƯƠNG VI. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT.
Phép tính luỹ thừa với số mũ nguyên, số mũ hữu tỉ, số mũ thực. Các tính chất.
Nhận biết:
– Nhận biết được khái niệm luỹ thừa với số mũ nguyên của một số thực khác 0; luỹ thừa với số mũ hữu tỉ và luỹ thừa với số mũ thực của một số thực dương.
Thông hiểu:
– Giải thích được các tính chất của phép tính luỹ thừa với số mũ nguyên, luỹ thừa với số mũ hữu tỉ và luỹ thừa với số mũ thực.
Vận dụng:
– Tính được giá trị biểu thức số có chứa phép tính luỹ thừa bằng sử dụng máy tính cầm tay.
– Giải quyết một số vấn đề có liên quan đến thực tiễn gắn với phép tính lũy thừa.
Phép tính lôgarit (logarithm). Các tính chất.
Nhận biết:
– Nhận biết được khái niệm lôgarit cơ số a (a > 0, a ≠ 1) của một số thực dương.
Thông hiểu:
– Giải thích được các tính chất của phép tính lôgarit nhờ sử dụng định nghĩa hoặc các tính chất đã biết trước đó.
Vận dụng:
– Tính được giá trị (đúng hoặc gần đúng) của lôgarit bằng cách sử dụng máy tính cầm tay.
– Sử dụng được tính chất của phép tính lôgarit trong tính toán các biểu thức số và rút gọn các biểu thức chứa biến (tính viết và tính nhẩm, tính nhanh một cách hợp lí).
Hàm số mũ. Hàm số lôgarit.
Nhận biết:
– Nhận biết được hàm số mũ và hàm số lôgarit.
– Nhận biết được sự liên quan giữa tính đồng biến, nghịch biến với cơ số của các hàm số mũ, hàm số lôgarit.
Thông hiểu:
– Tìm được tập xác định của hàm số mũ, hàm số lôgarit.
Phương trình, bất phương trình mũ và lôgarit.
Nhận biết:
– Nhận biết được phương trình, bất phương trình mũ, lôgarit.
– Nhận biết điều kiện phương trình, bất phương trình mũ, lôgarit.
Thông hiểu:
– Giải được phương trình, bất phương trình mũ, lôgarit ở dạng đơn giản.
Vận dụng:
– Giải quyết được một số vấn đề tương đối đơn giản có liên quan đến môn học khác hoặc có liên quan đến thực tiễn gắn với phương trình, bất phương trình mũ và lôgarit (ví dụ: bài toán liên quan đến độ pH, độ rung chấn).CHƯƠNG VII. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN.
Góc giữa hai đường thẳng. Hai đường thẳng vuông góc.
Nhận biết:
– Nhận biết được khái niệm góc giữa hai đường thẳng trong không gian.
– Nhận biết được hai đường thẳng vuông góc trong không gian.
Thông hiểu:
– Tính được góc giữa hai đường thẳng trong một số trường hợp đơn giản.
Đường thẳng vuông góc với mặt phẳng.
Nhận biết:
– Nhận biết được đường thẳng vuông góc với mặt phẳng.
Thông hiểu:
– Xác định được điều kiện để đường thẳng vuông góc với mặt phẳng.
– Giải thích được được mối liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng.
Vận dụng:
– Vận dụng được kiến thức về đường thẳng vuông góc với mặt phẳng để chứng minh 2 đường thẳng vuông góc.
Định lí ba đường vuông góc. Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng.
Nhận biết:
– Nhận biết được khái niệm phép chiếu vuông góc.
– Nhận biết được khái niệm góc giữa đường thẳng và mặt phẳng.
Thông hiểu:
– Xác định được hình chiếu vuông góc của một điểm, một đường thẳng, một tam giác.
– Giải thích được được định lí ba đường vuông góc.
– Xác định được góc giữa đường thẳng và mặt phẳng trong những trường hợp đơn giản (ví dụ: đã biết hình chiếu vuông góc của đường thẳng lên mặt phẳng).
Vận dụng:
– Tính được góc giữa đường thẳng và mặt phẳng trong những trường hợp đơn giản (ví dụ: đã biết hình chiếu vuông góc của đường thẳng lên mặt phẳng).
Hai mặt phẳng vuông góc. Hình lăng trụ đứng, lăng trụ đều, hình hộp đứng, hình hộp chữ nhật, hình lập phương, hình chóp đều. Góc nhị diện và góc phẳng nhị diện.
Nhận biết:
– Nhận biết được hai mặt phẳng vuông góc trong không gian.
– Nhận biết được khái niệm góc nhị diện, góc phẳng nhị diện.
Thông hiểu:
– Xác định được điều kiện để hai mặt phẳng vuông góc.
– Giải thích được tính chất cơ bản về hai mặt phẳng vuông góc.
– Giải thích được tính chất cơ bản của hình lăng trụ đứng, lăng trụ đều, hình hộp đứng, hình hộp chữ nhật, hình lập phương, hình chóp đều.
– Xác định được số đo góc nhị diện, góc phẳng nhị diện trong những trường hợp đơn giản (ví dụ: nhận biết được mặt phẳng vuông góc với cạnh nhị diện).
Vận dụng:
– Tính được số đo góc nhị diện, góc phẳng nhị diện trong những trường hợp đơn giản (ví dụ: nhận biết được mặt phẳng vuông góc với cạnh nhị diện).
Khoảng cách trong không gian.
Nhận biết:
– Nhận biết được khoảng cách từ một điểm đến một đường thằng.
– Nhận biết được đường vuông góc chung của hai đường thẳng chéo nhau.
– Nhận biết được khoảng cách từ một điểm đến một mặt phẳng.
Thông hiểu:
– Xác định được khoảng cách từ một điểm đến một đường thẳng; khoảng cách từ một điểm đến một mặt phẳng; khoảng cách giữa hai đường thẳng song song; khoảng cách giữa đường thẳng và mặt phẳng song song; khoảng cách giữa hai mặt phẳng song song trong những trường hợp đơn giản.
Vận dụng cao:
– Tính khoảng cách từ 1 điểm đến 1 mặt phẳng, khoảng cách giữa hai đường thẳng chéo nhau.

Be the first to comment