Bạn đang xem Giải bài tập SGK Giải tích 12 cơ bản: Ứng dụng của tích phân trong hình học. Cập nhật thêm đề thi thử, đề kiểm tra toán, học toán tại Toanpdf.com

Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Giải tích 12 cơ bản: Ứng dụng của tích phân trong hình học.CÂU HỎI VÀ BÀI TẬPBài 1. Tính diện tích hình phẳng giới hạn bởi các đường:
a) $y = {x^2}$, $y = x + 2.$
b) $y = |ln x|$, $y = 1.$
c) $y = {(x – 6)^2}$, $y = 6x – {x^2}.$Lời giải:
a) Xét phương trình:
${x^2} = x + 2$ $ Leftrightarrow {x^2} – x – 2 = 0$ $ Leftrightarrow x = – 1$, $x = 2.$Diện tích hình phẳng giới hạn bởi đường cong $y = {x^2}$ và đường thẳng $y = x + 2$ là:
$S = int_{ – 1}^2 {left| {{x^2} – (x + 2)} right|dx} $ $ = int_{ – 1}^2 {left| {{x^2} – x – 2} right|dx} .$
Vì ${x^2} – x – 2 le 0$ khi $ – 1 le x le 2.$
Nên: $S = – int_{ – 1}^2 {left( {{x^2} – x – 2} right)dx} $ $ = left. {left( { – frac{{{x^3}}}{3} + frac{{{x^2}}}{2} + 2x} right)} right|_{ – 1}^2$ $ = left( { – frac{8}{3} + 2 + 4} right) – left( {frac{1}{3} + frac{1}{2} – 2} right)$ $ = frac{9}{2}.$
Vậy $S = frac{9}{2}$ (đvdt).
b) Xét phương trình: $|ln x| = 1$ $ Leftrightarrow x = e$, $x = frac{1}{e}.$
Do đó diện tích cần tìm là: $S = int_{frac{1}{e}}^e {left| {left| {ln x} right| – 1} right|dx} .$
Ta có: $|ln x| = left{ {begin{array}{*{20}{l}}
{ln x:{rm{ nếu }}:x ge 1}\
{ – ln x:{rm{ nếu }}:0 < x le 1}
end{array}} right..$
Do đó:
$S = int_{frac{1}{e}}^e {left| {left| {ln x} right| – 1} right|dx} $ $ = int_{frac{1}{e}}^1 | ln x – 1|dx + int_1^e | – ln x – 1|dx$ $ = int_{frac{1}{e}}^1 {(1 – ln x)dx} + int_1^e {(ln x + 1)dx} $ (vì $ln x – 1 < 0$, $forall x in left[ {frac{1}{e};1} right]$ và $ – ln x – 1 < 0$, $forall x in [1;e]$).
$ Rightarrow S$ $ = int_{frac{1}{e}}^1 d x – int_{frac{1}{e}}^1 {ln xdx} + int_1^e {ln xdx} + int_1^e d x$ $ = left. x right|_{frac{1}{e}}^1 + left. x right|_1^e – int_{frac{1}{e}}^1 {ln xdx} + int_1^e {ln xdx} .$
$ = 1 – frac{1}{e} + e – 1$ $ – int_{frac{1}{e}}^1 {ln xdx} + int_1^e {ln xdx} $ $ = e – frac{1}{e}$ $ – left. {xln x} right|_{frac{1}{e}}^1 + int_{frac{1}{e}}^1 {dx} $ $ + left. {xln x} right|_1^e – int_1^e {dx} .$
$ = e – frac{1}{e} – frac{1}{e} + 1 – frac{1}{e} + e – e + 1$ $ = e – frac{3}{e} + 2$ (đvdt).
c) Xét phương trình:
${(x – 6)^2} = 6x – {x^2}$ $ Leftrightarrow 2{x^2} – 18x + 36 = 0$ $ Leftrightarrow x = 3$, $x = 6.$
Do đó diện tích cần tìm là:
$S = int_3^6 {left| {{{(x – 6)}^2} – left( {6x – {x^2}} right)} right|dx} $ $ = int_3^6 {left| {2{x^2} – 18x + 36} right|dx} $ $ = – 2int_3^6 {left( {{x^2} – 9x + 18} right)dx} $ (vì $2{x^2} – 18x + 36 le 0$ khi $3 le x le 6$).
$ = – left. {2left( {frac{{{x^3}}}{3} – frac{9}{2}{x^2} + 18x} right)} right|_3^6$ $ = – 2left( {18 – frac{{45}}{2}} right) = 9$ (đvdt).Bài 2. Tính diện tích hình phẳng giới hạn bởi các đường $y = {x^2} + 1$, tiếp tuyến với đường này tại điểm $M(2;5)$ và trục $Oy.$Lời giải:Ta lập phương trình tiếp tuyến với $y = {x^2} + 1$ tại $M$ ta có $y’ = 2x$ $ Rightarrow y'(2) = 4.$ Do đó phương trình tiếp tuyến với $y = {x^2} + 1$ tại $M(2;5)$ có phương trình là: $y = 4x – 3.$
Vậy diện tích cần tìm là: $S = int_0^2 {left[ {{x^2} + 1 – (4x – 3)} right]dx} .$
$ = int_0^2 {left( {{x^2} – 4x + 4} right)dx} $ $ = left. {left( {frac{1}{3}{x^3} – 2{x^2} + 4x} right)} right|_0^2$ $ = frac{8}{3} – 8 + 8 = frac{8}{3}$ (đvdt).Bài 3. Parabol $y = frac{{{x^2}}}{2}$ chia hình tròn có tâm tại gốc tọa độ bán kính $2sqrt 2 $ thành hai phần. Tìm tỉ số diện tích của chúng.Lời giải:Từ hình vẽ ta có:
${S_1} = 2int_0^2 {left( {sqrt {8 – {x^2}} – frac{{{x^2}}}{2}} right)dx} .$
$ = 2int_0^2 {sqrt {8 – {x^2}} } dx – int_0^2 {{x^2}} dx.$
$ = 2int_0^2 {sqrt {8 – {x^2}} } dx – left. {frac{{{x^3}}}{3}} right|_0^2$ $ = 2int_0^2 {sqrt {8 – {x^2}} } dx – frac{8}{3}.$
Đặt $x = 2sqrt 2 sin t$ $ Rightarrow dx = 2sqrt 2 cos tdt.$
Khi $x = 0$ thì $t = 0$; khi $x = 2$ thì $t = frac{pi }{4}.$
$ Rightarrow 2int_0^2 {sqrt {8 – {x^2}} } dx$ $ = 4sqrt 2 int_0^{frac{pi }{4}} {sqrt {8 – 8{{sin }^2}t} } .cos tdt$ $ = 16int_0^{frac{pi }{4}} {{{cos }^2}tdt} $ $ = 8int_0^{frac{pi }{4}} {(1 + cos 2t)dt} $ $ = 2pi + 4.$
$ Rightarrow {S_1} = 2pi + 4 – frac{8}{3}$ $ = frac{{6pi + 4}}{3}.$
Gọi $S$ là diện tích hình tròn tâm $O$ bán kính $R = 2sqrt 2 $ ta có $S = 8pi .$
Từ đó suy ra ${S_2} = S – {S_1}$ $ = 8pi – frac{{6pi + 4}}{3}$ $ = frac{{18pi – 4}}{3}.$
Vậy $frac{{{S_2}}}{{{S_1}}} = frac{{18pi – 4}}{{6pi + 4}} = frac{{9pi – 2}}{{3pi + 2}}.$Bài 4. Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh $Ox:$
a) $y = 1 – {x^2}$; $y = 0.$
b) $y = cos x$; $y = 0$; $x = 0$; $x = pi .$
c) $y = tan x$; $y = 0$; $x = 0$; $x = frac{pi }{4}.$Lời giải:
a) Xét phương trình: $1 – {x^2} = 0$ $ Leftrightarrow x = 1$, $x = – 1.$
Áp dụng công thức, ta có thể tích cần tìm là:
$V = pi int_{ – 1}^1 {{{left( {1 – {x^2}} right)}^2}} dx$ $ = pi int_{ – 1}^1 {left( {1 – 2{x^2} + {x^4}} right)dx} .$
$ = left. {pi left( {x – frac{2}{3}{x^3} + frac{{{x^5}}}{5}} right)} right|_{ – 1}^1$ $ = pi left[ {left( {1 – frac{2}{3} + frac{1}{5}} right) – left( { – 1 + frac{2}{3} – frac{1}{5}} right)} right]$ $ = pi left( {2 – frac{4}{3} + frac{2}{5}} right)$ $ = frac{{16pi }}{{15}}.$
b) Áp dụng công thức, ta có:
$V = pi int_0^pi {{{cos }^2}xdx} $ $ = pi int_0^pi {frac{{1 + cos 2x}}{2}dx} $ $ = frac{pi }{2}int_0^pi d x + frac{pi }{4}int_0^pi {cos 2xd2x} $ $ = left. {frac{pi }{2}x} right|_0^pi + left. {frac{pi }{4}sin 2x} right|_0^pi $ $ = frac{{{pi ^2}}}{2}.$
c) Áp dụng công thức, ta có:
$V = pi int_0^{frac{pi }{4}} {{{tan }^2}xdx} $ $ = pi int_0^{frac{pi }{4}} {left( {frac{1}{{{{cos }^2}x}} – 1} right)dx} $ $ = pi int_0^{frac{pi }{4}} {frac{{dx}}{{{{cos }^2}x}}} – pi int_0^{frac{pi }{4}} {dx} .$
$ = left. {pi tan x} right|_0^{frac{pi }{4}} – left. {pi x} right|_0^{frac{pi }{4}}$ $ = pi – frac{{{pi ^2}}}{4}$ $ = pi left( {1 – frac{pi }{4}} right).$Bài 5. Cho tam giác vuông $OPM$ có cạnh $OP$ nằm trên $Ox.$ Đặt $widehat {POM} = alpha $, $OM = R$ (${0 le alpha le frac{pi }{3}}$, $R > 0$). Gọi $V$ là khối tròn xoay thu được khi quay tam giác đó xung quanh trục $Ox.$
a) Tính thể tích của $V$ theo $alpha $ và $R.$
b) Tìm $alpha $ sao cho thể tích của $V$ lớn nhất.Lời giải: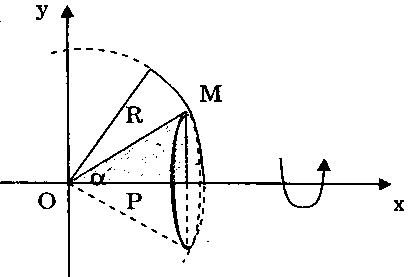a) Ta có: $OP = Rcos alpha $, $PM = Rsin alpha .$
Suy ra diện tích đáy $B$ của khối tròn xoay $V$ là: $B = pi P{M^2} = pi {R^2}{sin ^2}alpha .$
Theo công thức, ta có thể tích của khối tròn xoay $V$ là:
$V = frac{1}{3}B.OP$ $ = frac{1}{3}.R.cos alpha .pi .{R^2}{sin ^2}alpha $ $ = frac{1}{3}pi {R^3}cos alpha .{sin ^2}alpha $ $ = frac{1}{3}pi {R^3}left( {cos alpha – {{cos }^3}alpha } right)$ với $0 le alpha le frac{pi }{3}.$
b) Ta có $V$ lớn nhất $ Leftrightarrow cos alpha – {cos ^3}alpha $ lớn nhất.
Xét hàm số $f(t) = t – {t^3}$ $(t = cos alpha ).$
Khi $alpha in left( {0;frac{pi }{3}} right)$ thì $t in left( {frac{1}{2};1} right).$
Ta có: $f'(t) = 1 – 3{t^2} = 0$ $ Leftrightarrow t = frac{1}{{sqrt 3 }}$ $left( {frac{1}{2} < t < 1} right).$
Ta có bảng biến thiên:Suy ra $f(t)$ lớn nhất bằng $frac{2}{{3sqrt 3 }}$ khi $t = frac{1}{{sqrt 3 }}.$
Hay $cos alpha – {cos ^3}alpha $ lớn nhất: $frac{2}{{3sqrt 3 }}$ đạt được khi $cos alpha = frac{1}{{sqrt 3 }}.$
Vậy ${V_{max {rm{ }}}} = frac{{2pi sqrt 3 }}{{27}}{R^3}$ khi $cos alpha = frac{1}{{sqrt 3 }}.$