Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Giải tích 12 nâng cao: Cực trị của hàm số.CÂU HỎI VÀ BÀI TẬPBài 11. Tìm cực trị của các hàm số sau:
a) $f(x) = frac{1}{3}{x^3} + 2{x^2} + 3x – 1.$
b) $f(x) = frac{1}{3}{x^3} – {x^2} + 2x – 10.$
c) $f(x) = x + frac{1}{x}.$
d) $f(x) = |x|(x + 2).$
e) $f(x) = frac{{{x^5}}}{5} – frac{{{x^3}}}{3} + 2.$
f) $f(x) = frac{{{x^2} – 3x + 2}}{{x – 1}}.$a) Hàm số đã cho xác định trên $R.$
Ta có: $f'(x) = {x^2} + 4x + 3.$
Từ đó $f'(x) = 0$ $ Leftrightarrow x = – 1$ hoặc $x = – 3.$
Cách 1. Bảng biến thiên:
Vậy hàm số đạt cực đại tại điểm $x = -3$, giá trị cực đại của hàm số là ${f_{CĐ}} = f( – 3) = – 1$, hàm số đạt cực tiểu tại điểm $x = -1$, giá trị cực tiểu của hàm số là ${f_{CT}} = f( – 1) = – frac{7}{3}.$
Cách 2. $f”(x) = 2x + 4$ $ Rightarrow f”( – 3) = – 2 < 0$, $f”( – 1) = 2 > 0.$
Vậy hàm số đạt cực đại tại điểm $x = -3$, giá trị cực đại của hàm số là: ${f_{CĐ}} = f( – 3) = – 1$, hàm số đạt cực tiểu tại điểm $x = -1$, ${f_{CT}} = f( – 1) = – frac{7}{3}.$
b) Tập xác định: $R.$
$f'(x) = {x^2} – 2x + 2$ $ = {(x – 1)^2} + 1 > 0$, $forall x in R$ $ Rightarrow f(x)$ luôn đồng biến nên hàm số không có cực trị.
c) Tập xác định: $Rbackslash 0} .$
$f'(x) = 1 – frac{1}{{{x^2}}}$ $ = frac{{{x^2} – 1}}{{{x^2}}}$, $f'(x) = 0$ $ Leftrightarrow x = pm 1.$
Cách 1. Bảng biến thiên:
Vậy hàm số đạt cực đại tại $x = – 1$, ${f_{CĐ}} = f( – 1) = – 2$, hàm số đạt cực tiểu tại $x = 1$, ${f_{CT}} = f(1) = 2.$
Cách 2. $f”(x) = frac{{2x}}{{{x^4}}} = frac{2}{{{x^3}}}.$
Vì $f”(x) = – 2 < 0$ nên hàm số đạt cực đại tại $x = – 1$, ${f_{CĐ}} = f( – 1) = – 2.$ $f”(1) = 2 > 0$ nên hàm số đạt cực tiểu tại $x = 1$, ${f_{CT}} = f(1) = 2.$
d) $f(x)$ xác định và liên tục trên $R.$
Ta có: $f(x) = left{ {begin{array}{*{20}{l}}
{x(x + 2)}&{{rm{với}}:x ge 0}\
{ – x(x + 2)}&{{rm{với}}:x < 0}
end{array}} right.$ $ Rightarrow f'(x) = left{ {begin{array}{*{20}{l}}
{2x + 2}&{{rm{với}}:x > 0}\
{ – 2x – 2}&{{rm{với}}:x < 0}
end{array}} right..$
Bảng biến thiên: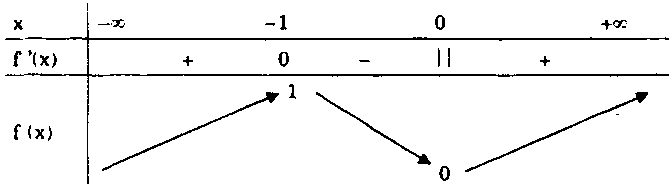
Hàm số đạt cực đại tại $x = – 1$, ${f_{CĐ}} = f( – 1) = 1.$
Hàm số đạt cực tiểu tại $x = 0$, ${f_{CT}} = f(0) = 1.$
e) Tập xác định: $R.$
$f'(x) = {x^4} – {x^2}$, $f'(x) = 0$ $ Leftrightarrow x = 0$ hoặc $x = pm 1.$
Bảng biến thiên:
Vậy:
Hàm số đạt cực đại tại $x = – 1$, ${f_{CĐ}} = f( – 1) = frac{{32}}{{15}}.$
Hàm số đạt cực tiểu tại $x = 1$, ${f_{CT}} = f(1) = frac{{28}}{{15}}.$
f) Tập xác định: $Rbackslash { 1} .$
Ta có: $f'(x) = frac{{(2x – 3)(x – 1) – left( {{x^2} – 3x + 3} right)}}{{{{(x – 1)}^2}}}$ $ = frac{{{x^2} – 2x}}{{{{(x – 1)}^2}}}.$
$f'(x) = 0$ $ Leftrightarrow x = 0$ hoặc $x = 2.$
Bảng biến thiên:
Vậy:
Hàm số đạt cực đại tại $x = 0$, ${f_{CĐ}} = f(0) = – 3.$
Hàm số đạt cực tiểu tại $x = 2$, ${f_{CT}} = f(2) = 1.$Bài 12. Tìm cực trị của các hàm số sau:
a) $y = xsqrt {4 – {x^2}} .$
b) $y = sqrt {8 – {x^2}} .$
c) $y = x – sin 2x + 2.$
d) $y = 3 – 2cos x – cos 2x.$a) Tập xác định: $[ – 2;2].$
$y’ = sqrt {4 – {x^2}} + xfrac{{ – 2x}}{{2sqrt {4 – {x^2}} }}$ $ = frac{{4 – 2{x^2}}}{{sqrt {4 – {x^2}} }}.$
$y’ = 0$ $ Leftrightarrow x = pm sqrt 2 .$
Bảng biến thiên:
Hàm số đạt cực tiểu tại $x = – sqrt 2 $, ${y_{CT}} = y( – sqrt 2 ) = – 2.$
Hàm số đạt cực đại tại $x = sqrt 2 $, ${y_{CĐ}} = y(sqrt 2 ) = 2.$
b) Tập xác định: $[ – 2sqrt 2 ;2sqrt 2 ].$
$y’ = frac{{ – x}}{{sqrt {8 – {x^2}} }}$, $y’ = 0$ $ Leftrightarrow x = 0.$
Bảng biến thiên:
Vậy:
Hàm số đạt cực đại tại $x = 0$, ${y_{CĐ}} = y(0) = 2sqrt 2 .$
Hàm số không có cực tiểu.
c) Tập xác định: $R.$
$y’ = (x – sin 2x + 2)’$ $ = 1 – 2cos 2x.$
$y’ = 0$ $ Leftrightarrow 1 – 2cos 2x = 0$ $ Leftrightarrow x = pm frac{pi }{6} + kpi $, $k in Z.$
$y” = 4sin 2x.$
Ta có: $y”left( {frac{pi }{6} + kpi } right)$ $ = 4sin left( {frac{pi }{3} + k2pi } right)$ $ = 2sqrt 3 > 0.$
$y”left( { – frac{pi }{6} + kpi } right)$ $ = 4sin left( { – frac{pi }{3} + k2pi } right)$ $ = – 2sqrt 3 < 0.$
Vậy hàm số đạt cực đại tại các điểm $x = – frac{pi }{6} + kpi $, $k in Z.$
${y_{CĐ}} = yleft( {frac{pi }{6} + kpi } right)$ $ = 2 + frac{{sqrt 3 }}{2} – frac{pi }{6} + kpi $, $k in Z.$
Hàm số đạt cực tiểu tại điểm $x = frac{pi }{6} + kpi $, $k in Z.$
${y_{CT}} = yleft( {frac{pi }{6} + kpi } right)$ $ = 2 – frac{{sqrt 3 }}{2} + frac{pi }{6} + kpi $, $k in Z.$
d) Tập xác định: $R.$
$y’ = 2sin x + 2sin 2x$ $ = 2sin x(1 + 2cos x).$
$y’ = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{sin x = 0}\
{cos x = – frac{1}{2}}
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = kpi }\
{x = pm frac{{2pi }}{3} + k2pi }
end{array}} right.$ ($k in Z$).
$y” = 2cos x + 4cos 2x.$
Ta có: $y”(kpi ) = left{ {begin{array}{*{20}{l}}
{2:{rm{nếu}}:k:{rm{lẻ}}}\
{6:{rm{nếu}}:k:{rm{chẵn}}}
end{array}} right.$ $ Rightarrow y”(kpi ) > 0$ (có thể viết: ${y”(kpi ) = 4 + 2cos kpi }$).
Nên hàm số đạt cực tiểu tại các điểm $x = kpi $, ${y_{CT}} = y(kx)$ $ = left{ {begin{array}{*{20}{l}}
{0:{rm{nếu}}:k:{rm{chẵn}}}\
{4:{rm{nếu}}:k:{rm{lẻ}}}
end{array}} right..$
$y”left( { pm frac{{2pi }}{3} + k2pi } right) = – 3 < 0$ nên hàm số đạt cực đại tại các điểm: $x = pm frac{{2pi }}{3} + k2pi $, $k in Z$, ${y_{CĐ}} = yleft( { pm frac{{2pi }}{3} + k2pi } right) = frac{9}{2}.$Bài 13. Tìm các hệ số $a$, $b$, $c$, $d$ của hàm số $f(x) = a{x^3} + b{x^2} + cx + d$ sao cho hàm số $f$ đạt cực tiểu tại điểm $x = 0$, $f(0) = 0$ và đạt cực đại tại điểm $x = 1$, $f(1) = 1.$Ta có $f'(x) = 3a{x^2} + 2bx + c$ $ Rightarrow f'(0) = c$, $f'(1) = 3a + 2b + c.$
Vì $f(0) = 0$ $ Rightarrow d = 0.$
Hàm số đạt cực tiểu tại $x = 0$ nên $f'(0) = 0$ $ Rightarrow c = 0$, $f(1) = 1$ $ Rightarrow a + b = 1.$
Hàm số đạt cực đại tại điểm $x = 1$ nên $f'(1) = 0$ $ Rightarrow 3a + 2b = 0.$
Giải hệ: $left{ {begin{array}{*{20}{l}}
{a + b = 1}\
{3a + 2b = 0}
end{array}} right.$ ta được $a = – 2$, $b = 3.$
Vậy $f(x) = – 2{x^3} + 3{x^2}.$
Thử lại $f'(x) = – 6{x^2} + 6x$, $f”(x) = – 12x + 6.$
$f”(0) = 6 > 0.$ Hàm số đạt cực tiểu tại điểm $x = 0.$
$f”(1) = – 6 < 0.$ Hàm số đạt cực đại tại $x = 1.$
Đáp số: $a = -2$, $b = 3$, $c = 0$, $d = 0.$ Bài 14. Xác định các hệ số $a$, $b$, $c$ sao cho hàm số $f(x) = {x^3} + a{x^2} + bx + c$ đạt cực trị bằng $0$ tại $x = -2$ và đồ thị của hàm số đi qua $A(1;0).$Cách 1. $f'(x) = 3{x^2} + 2ax + b.$
Điều kiện cần:
Hàm số đạt cực trị bằng $0$ tại $x = – 2$ $ Rightarrow f'( – 2) = 0$ $f( – 2) = 0.$
Hay $ – 4a + b + 12 = 0$ $(1)$ và $4a – 2b + c – 8 = 0$ $(2).$
Đồ thị đi qua $A(1;0)$ $ Rightarrow a + b + c + 1 = 0.$
Giải hệ gồm ba phương trình $(1)$, $(2)$, $(3)$ ta được $a = 3$, $b = 0$, $c = -4.$
Điều kiện đủ:
Xét $f(x) = {x^3} + 3{x^2} – 4.$
Ta có: đồ thị hàm số $f(x)$ đi qua $A(1;0).$
$f'(x) = 3{x^2} + 6x$ $ Rightarrow f”(x) = 6x + 6.$
$f'( – 2) = 0$, $f”( – 2) = – 6 < 0$ nên $x = – 2$ là điểm cực đại và $f( – 2) = 0.$
Đáp số: $a = 3$, $b = 0$, $c = -4.$
Cách 2. Hướng dẫn:
Yêu cầu bài toán tương đương với: $f( – 2) = 0$, $f'( – 2) = 0$, $f(1) = 0$, phương trình $f'(x) = 0$ có hai nghiệm phân biệt trong đó có một nghiệm $x = -2.$ Bài 15. Chứng minh rằng với mọi giá trị của $m$, hàm số $y = frac{{{x^2} – m(m + 1)x + {m^3} + 1}}{{x – m}}$ luôn có cực đại và cực tiểu.Hàm số được viết lại là: $y = x – {m^2} + frac{1}{{x – m}}$, hàm số xác định với mọi $x ne m.$
$y’ = 1 – frac{1}{{{{(x – m)}^2}}}$ với $x ne m$, $y’ = 0$ $ Leftrightarrow {(x – m)^2} = 1$ $ Leftrightarrow x = m – 1$ hoặc $x = m + 1.$
Bảng biến thiên:
Vậy với mọi giá trị của $m$, hàm số đạt cực đại tại $x = m -1$ và đạt cực tiểu tại $x = m + 1.$
Để lại một phản hồi