
Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Hình học 12 cơ bản: Mặt cầu.CÂU HỎI VÀ BÀI TẬPBài 1. Tìm tập hợp tất cả những điểm $M$ trong không gian luôn nhìn đoạn thẳng $AB$ cố định dưới một góc vuông.Lời giải: Gọi $O$ là trung điểm của $AB.$
Gọi $O$ là trung điểm của $AB.$
Xét tam giác vuông $MAB$, vuông tại $M$, ta có:
$OM = OA = OB = frac{{AB}}{2}.$
Do $O$ cố định, $frac{{AB}}{2}$ là số không đổi, nên tập hợp các điểm $M$ trong không gian nhìn $AB$ dưới một góc vuông là mặt cầu tâm $O$, bán kính $r = frac{{AB}}{2}.$Bài 2. Cho hình chóp tứ giác đều $S.ABCD$ có tất cả các cạnh đều bằng $a.$ Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp đó.Lời giải: Do $S.ABCD$ là hình chóp tứ giác đều nên $ABCD$ là hình vuông và chân đường cao của $S.ABCD$ trùng với tâm $I$ của $ABCD$, tức là $SI bot (ABCD).$
Do $S.ABCD$ là hình chóp tứ giác đều nên $ABCD$ là hình vuông và chân đường cao của $S.ABCD$ trùng với tâm $I$ của $ABCD$, tức là $SI bot (ABCD).$
Xét tam giác vuông $SIA$ có:
$IA = frac{1}{2}AC = frac{{asqrt 2 }}{2}.$
$SI = sqrt {S{A^2} – I{A^2}} = frac{{asqrt 2 }}{2}.$
$ Rightarrow SI = IA = IB = IC = ID = frac{{asqrt 2 }}{2}.$
Vậy mặt cầu ngoại tiếp hình chóp có tâm là $I$, và bán kính $r = frac{{asqrt 2 }}{2}.$Bài 3. Tìm tập hợp tâm các mặt cầu luôn luôn chứa một đường tròn cố định cho trước.Lời giải: Gọi đường tròn $(C)$ tâm $O$ bán kính $r$ cố định cho trước và nằm trên mặt phẳng $(alpha )$ cố định.
Gọi đường tròn $(C)$ tâm $O$ bán kính $r$ cố định cho trước và nằm trên mặt phẳng $(alpha )$ cố định.
Gọi $I$ là tâm của mặt cầu $(S)$ đi qua đường tròn $(C).$ Khi đó mặt cầu $(S)$ cắt mặt phẳng $(alpha )$ theo giao tuyến là đường tròn $(C)$ nên $O$ là hình chiếu vuông góc của $I$ trên $(alpha )$, hay $IO bot mp(alpha ).$
Suy ra $I$ nằm trên đường thẳng $Delta $ vuông góc với $mp(alpha )$ tại $O.$
Ngược lại, với mọi điểm $I in Delta $, ta có: Khoảng cách từ $I$ đến mọi điểm trên $(C)$ đều bằng nhau. Suy ra $I$ là tâm mặt cầu $(S)$ luôn đi qua $(C).$
Vậy: Tập hợp tâm các mặt cầu luôn chứa đường tròn cố định cho trước là đường thẳng $Delta $ vuông góc với mặt phẳng chứa đường tròn đó tại tâm của nó.Bài 4. Tìm tập hợp tâm những mặt cầu luôn cùng tiếp xúc với ba cạnh của một tam giác cho trước.Lời giải: Giả sử mặt cầu $S(O;r)$ tiếp xúc với ba cạnh $BC$, $AC$, $AB$ của tam giác $ABC$ lần lượt tại $A’$, $B’$, $C’.$ Gọi $I$ là hình chiếu vuông góc của $O$ lên mặt phẳng $(ABC).$
Giả sử mặt cầu $S(O;r)$ tiếp xúc với ba cạnh $BC$, $AC$, $AB$ của tam giác $ABC$ lần lượt tại $A’$, $B’$, $C’.$ Gọi $I$ là hình chiếu vuông góc của $O$ lên mặt phẳng $(ABC).$
Vì $OA’ bot BC$ nên $IA’ bot BC$; tương tự $IB’ bot AC$ nên $IC’ bot AB.$
$ Rightarrow IA’ = IB’ = IC’ = r’$ hay $I$ là tâm đường tròn nội tiếp tam giác $ABC.$
Vậy $O$ thuộc trục đường tròn nội tiếp của tam giác $ABC.$
Đảo lại, nếu lấy $O$ thuộc trục $Delta $ của đường tròn nội tiếp tam giác $ABC$ thì ta có: $IA’ = IB’ = IC’$, do đó $OA’ = OB’ = OC’ = r.$
Suy ra, mặt cầu $S(O;r)$ tiếp xúc với ba cạnh của tam giác $ABC.$
Vậy: Tập hợp tâm những mặt cầu cùng tiếp xúc với ba cạnh của một tam giác cho trước là trục của đường tròn nội tiếp tam giác cho trước. Bài 5. Từ một điểm $M$ nằm ngoài mặt cầu $S(O;r)$ ta kẻ hai đường thẳng cắt mặt cầu lần lượt tại $A$, $B$ và $C$, $D.$
a) Chứng minh rằng $MA.MB = MC.MD.$
b) Gọi $MO = d.$ Tính $MA.MB$ theo $d$ và $r.$Lời giải: a) Gọi $(alpha )$ là mặt phẳng chứa $MA$ và $MC$, ta có:
a) Gọi $(alpha )$ là mặt phẳng chứa $MA$ và $MC$, ta có:
Mặt phẳng $(alpha )$ cắt mặt cầu $S(O;r)$ theo một đường tròn $(V)$ và $A$, $B$, $C$, $D$ thuộc $(V).$
Ta có: $Delta MAC$ đồng dạng $Delta MDB$ $ Rightarrow frac{{MA}}{{MD}} = frac{{MC}}{{MB}}.$
$ Rightarrow MA.MB = MC.MD.$
b) Gọi $I$ là trung điểm của $AB$ thì $IO bot AB$ (vì $OA = OB = r$).
Ta có: $MA.MB$ $ = (MI – IA)(MI + IB)$ $ = M{I^2} – I{A^2}$ $ = left( {M{O^2} – O{I^2}} right) – left( {O{A^2} – O{I^2}} right)$ $ = M{O^2} – O{A^2} = {d^2} – {r^2}.$ Vậy $MA.MB = {d^2} – {r^2}.$Bài 6. Cho mặt cầu $S(O;r)$ tiếp xúc với mặt phẳng $(P)$ tại $I.$ Gọi $M$ là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với $I$ qua tâm $O.$ Từ $M$ kẻ hai tiếp tuyến của mặt cầu cắt $(P)$ tại $A$ và $B.$ Chứng minh rằng $widehat {AMB} = widehat {AIB}.$Lời giải: Vì mặt phẳng $(P)$ tiếp xúc với mặt cầu $S(O;r)$ tại $I$ nên $AI$ và $BI$ là hai tiếp tuyến với mặt cầu $S(O;r).$
Vì mặt phẳng $(P)$ tiếp xúc với mặt cầu $S(O;r)$ tại $I$ nên $AI$ và $BI$ là hai tiếp tuyến với mặt cầu $S(O;r).$
Vì $AM$ và $AI$ là hai tiếp tuyến của mặt cầu kẻ từ $A$ nên: $MA = AI$, tương tự ta có: $BM = BI$ $ Rightarrow Delta AMB = Delta AIB$ (c – c – c).
Vậy $widehat {AMB} = widehat {AIB}.$Bài 7. Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ có $AA’ = a$, $AB = b$, $AD = c.$
a) Xác định tâm và bán kính mặt cầu đi qua $8$ đỉnh của hình hộp đó.
b) Tính bán kính của đường tròn là giao tuyến của mặt phẳng $(ABCD)$ với mặt cầu nói trên. Lời giải: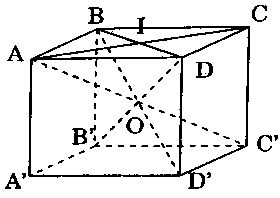 a) Vì các đường chéo của hình hộp chữ nhật bằng nhau và cắt nhau tại trung điểm $O$ của mỗi đường nên:
a) Vì các đường chéo của hình hộp chữ nhật bằng nhau và cắt nhau tại trung điểm $O$ của mỗi đường nên:
$OA = OB = OC = OD$ $ = OA’ = OB’ = OC’ = OD’ = r.$
Suy ra $O$ là tâm mặt cầu đi qua tám đỉnh của hình hộp chữ nhật.
Ta có: $AC{‘^2} = AA{‘^2} + A’C{‘^2}$ $ = AA{‘^2} + A’B{‘^2} + A’D{‘^2}.$
$AC{‘^2} = {a^2} + {b^2} + {c^2}.$
$ Rightarrow r = frac{1}{2}AC’$ $ = frac{1}{2}sqrt {{a^2} + {b^2} + {c^2}} .$
b) Đường tròn giao tuyến của mặt phẳng $(ABCD)$ và mặt cầu nói trên là đường tròn ngoại tiếp hình chữ nhật $ABCD.$
Gọi $I$ là giao của hai đường chéo $AC$ và $BD$, ta có: $IA = IB = IC = ID = r’.$
$ Rightarrow r’ = frac{{AC}}{2}$ $ = frac{1}{2}sqrt {A{B^2} + A{D^2}} $ $ = frac{1}{2}sqrt {{b^2} + {c^2}} .$
Vậy $r’ = frac{1}{2}sqrt {{b^2} + {c^2}} .$Bài 8. Chứng minh rằng nếu có mặt cầu tiếp xúc với $6$ cạnh của một hình tứ diện thì tổng độ dài của các cặp cạnh đối diện của tứ diện bằng nhau.Lời giải: Giả sử có mặt cầu $(S)$ tiếp xúc với các cạnh $AB$, $AC$, $AD$, $CB$, $CD$, $BD$ lần lượt tại $M$, $N$, $P$, $Q$, $R$, $S.$ Khi ấy $AM$, $AN$, $AP$ là tiếp tuyến của mặt cầu $(S)$ kẻ từ $A$ nên:
Giả sử có mặt cầu $(S)$ tiếp xúc với các cạnh $AB$, $AC$, $AD$, $CB$, $CD$, $BD$ lần lượt tại $M$, $N$, $P$, $Q$, $R$, $S.$ Khi ấy $AM$, $AN$, $AP$ là tiếp tuyến của mặt cầu $(S)$ kẻ từ $A$ nên:
$AM = AN = AP = a.$
Tương tự, ta có:
$BM = BQ = BS = b.$
$CQ = CN = CR = c.$
$DP = DR = DS = d.$
$ Rightarrow AB + CD$ $ = AM + BM + CR + DR$ $ = a + b + c + d.$
Tương tự, ta có:
$AC + BD = a + b + c + d.$
$AD + BC = a + b + c + d.$
Vậy tổng các cặp cạnh đối của tứ diện thì bằng nhau.Bài 9. Cho một điểm $A$ cố định và một đường thẳng $a$ cố định không đi qua $A.$ Gọi $O$ là một điểm thay đổi trên $a.$ Chứng minh rằng mặt cầu tâm $O$ bán kính $r = OA$ luôn đi qua một đường tròn cố định. Lời giải: Gọi $(alpha )$ là mặt phẳng qua $A$ và vuông góc với $a$ tại $I.$ Ta có mặt phẳng $(alpha )$ cố định và điểm $I$ cũng cố định.
Gọi $(alpha )$ là mặt phẳng qua $A$ và vuông góc với $a$ tại $I.$ Ta có mặt phẳng $(alpha )$ cố định và điểm $I$ cũng cố định.
Mặt phẳng $(alpha )$ cắt mặt cầu $S(O;r)$ theo đường tròn $C(I;IA)$ cố định, vì $(C)$ nằm trong mặt phẳng $(alpha )$ cố định, tâm $I$ cố định, $IA$ không đổi.
Vậy mặt cầu $S(O;r)$ luôn đi qua đường tròn cố định $C(I;IA).$Bài 10. Cho hình chóp $S.ABC$ có $4$ đỉnh đều nằm trên một mặt cầu, $SA = a$, $SB = b$, $SC = c$ và cạnh $SA$, $SB$, $SC$ đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo bởi mặt cầu đó. Lời giải: Gọi $M$ là trung điểm của $BC$, qua $M$ kẻ trục $Delta $ của tam giác $SBC$ thì $Delta //SA.$
Gọi $M$ là trung điểm của $BC$, qua $M$ kẻ trục $Delta $ của tam giác $SBC$ thì $Delta //SA.$
Kẻ mặt phẳng trung trực của $SA$ cắt $Delta $ tại $I$, ta có $I$ là tâm của mặt cầu ngoại tiếp hình chóp $SABC.$
$IA = IB = IC = IS = r.$
Bán kính mặt cầu là: $r = IS = sqrt {I{M^2} + O{M^2}} .$
$r = frac{1}{2}sqrt {{a^2} + {b^2} + {c^2}} .$
Diện tích mặt cầu là: $S = 4pi {r^2} = pi left( {{a^2} + {b^2} + {c^2}} right).$
Thể tích khối cầu là: $V = frac{4}{3}.pi .{r^3}$ $ = frac{pi }{6}left( {{a^2} + {b^2} + {c^2}} right)sqrt {{a^2} + {b^2} + {c^2}} .$

Be the first to comment