Bài viết trình bày định nghĩa, định lý, các quy tắc và phương pháp tìm giới hạn của dãy số cùng các ví dụ minh họa có hướng dẫn giải.A. LÝ THUYẾT CẦN NẮM
1. Giới hạn hữu hạn của dãy số
a. Định nghĩa:
• $lim {u_n} = 0$ $ Leftrightarrow forall varepsilon > 0$, $exists {n_0} in N^*$: $left| {{u_n}} right| < varepsilon $, $forall n > {n_0}.$
• $lim {u_n} = a$ $ Leftrightarrow lim left( {{u_n} – a} right) = 0.$
b. Một số giới hạn hữu hạn thường gặp:
• $lim frac{1}{{{n^k}}} = 0$ với mọi $k in N^* .$
• Nếu $left| q right| < 1$ thì $lim {q^n} = 0.$
• Nếu ${u_n} = c$ (với $c$ là hằng số) thì $lim {u_n}$ $ = lim c = c.$
2. Một số định lí về giới hạn của dãy số
• Nếu dãy số $left( {{u_n}} right)$ thỏa $left| {{u_n}} right| < {v_n}$ kể từ số hạng nào đó trở đi và $lim {v_n} = 0$ thì $lim {u_n} = 0.$
• Cho $lim {u_n} = a$, $lim {v_n} = b$. Ta có:
$lim ({u_n} + {v_n}) = a + b.$
$lim ({u_n} – {v_n}) = a – b.$
$lim ({u_n}.{v_n}) = a.b$
$lim frac{{{u_n}}}{{{v_n}}} = frac{a}{b}$ $(b ne 0).$
Nếu ${u_n} ge 0$, $forall n$ thì $lim sqrt {{u_n}} = sqrt a .$
3. Tổng của cấp số nhân lùi vô hạn
Cho cấp số nhân $({u_n})$ có công bội $q$ thỏa $left| q right| < 1.$ Khi đó tổng $S = {u_1} + {u_2} + … + {u_n} + …$ $ = frac{{{u_1}}}{{1 – q}}.$
4. Giới hạn vô cực
a. Định nghĩa:
• $lim {u_n} = + infty $ $ Leftrightarrow forall M > 0$, $exists {n_0} in {N^*}$: ${u_n} > M$, $forall n > {n_0}.$
• $lim {u_n} = – infty $ $ Leftrightarrow lim left( { – {u_n}} right) = + infty .$
b. Một số giới hạn vô cực thường gặp:
• $lim {n^k} = + infty $ với mọi $k > 0.$
• $lim {q^n} = + infty $ với mọi $q > 1.$
c. Một vài quy tắc tìm giới hạn vô cực:
Quy tắc 1: Nếu $lim {u_n} = pm infty $, $lim {v_n} = pm infty $ thì $lim ({u_n}.{v_n})$ được tính như sau: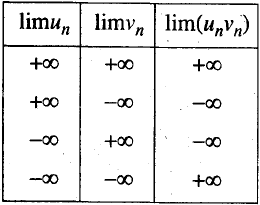
Quy tắc 2: Nếu $lim {u_n} = pm infty $, $lim {v_n} = L ≠ 0$ thì $lim ({u_n}.{v_n})$ được tính như sau:
Quy tắc 3: Nếu $lim {u_n} = L ≠ 0$, $lim {v_n} = 0$ và ${v_n} > 0$ hoặc ${v_n} < 0$ kể từ một số hạng nào đó trở đi thì $lim frac{{{u_n}}}{{{v_n}}}$ được tính như sau:
B. PHƯƠNG PHÁP TÌM GIỚI HẠN CỦA DÃY SỐ
Dạng toán 1. Tìm giới hạn bằng định nghĩa.
Phương pháp:
• Để chứng minh $lim {u_n} = 0$ ta chứng minh với mọi số $a > 0$ nhỏ tùy ý luôn tồn tại một số ${n_a}$ sao cho $left| {{u_n}} right| < a$, $forall n > {n_a}.$
• Để chứng minh $lim {u_n} = L$ ta chứng minh $lim ({u_n} – L) = 0.$
• Để chứng minh $lim {u_n} = + infty $ ta chứng minh với mọi số $M > 0$ lớn tùy ý, luôn tồn tại số tự nhiên ${n_M}$ sao cho ${u_n} > M$, $forall n > {n_M}.$
• Để chứng minh $lim {u_n} = – infty $ ta chứng minh $lim ( – {u_n}) = + infty .$
• Một dãy số nếu có giới hạn thì giới hạn đó là duy nhất.Ví dụ 1. Chứng minh rằng:
1. $lim frac{{n + 2}}{{n + 1}} = 1.$
2. $lim frac{{{n^2} – 1}}{{2{n^2} + 1}} = frac{1}{2}.$
3. $lim frac{{1 – 2n}}{{sqrt {{n^2} + 1} }} = – 2.$1. Với $a > 0$ nhỏ tùy ý, ta chọn ${n_a} > frac{1}{a} – 1$, ta có:
$left| {frac{{n + 2}}{{n + 1}} – 1} right|$ $ = frac{1}{{n + 1}} < frac{1}{{{n_a} + 1}} < a$ với $forall n > {n_a}.$
Suy ra $lim left| {frac{{n + 2}}{{n + 1}} – 1} right| = 0$ $ Rightarrow lim frac{{n + 2}}{{n + 1}} = 1.$
2. Với $a > 0$ nhỏ tùy ý, ta chọn ${n_a} > sqrt {frac{3}{a} – 1} $, ta có:
$left| {frac{{{n^2} – 1}}{{2{n^2} + 1}} – frac{1}{2}} right|$ $ = frac{3}{{{n^2} + 1}}$ $ < frac{3}{{n_a^2 + 1}} < a$ với $forall n > {n_a}.$
Suy ra $lim left| {frac{{{n^2} – 1}}{{2{n^2} + 1}} – frac{1}{2}} right| = 0$ $ Rightarrow lim frac{{{n^2} – 1}}{{2{n^2} + 1}} = frac{1}{2}.$
3. Với $a > 0$ nhỏ tùy ý, ta chọn ${n_a} > sqrt {frac{9}{{{a^2}}} – 1} $, ta có:
$left| {frac{{1 – 2n}}{{sqrt {{n^2} + 1} }} + 2} right|$ $ = left| {frac{{1 – 2n + 2sqrt {{n^2} + 1} }}{{sqrt {{n^2} + 1} }}} right|$ $ < left| {frac{{1 – 2n + 2(n + 1)}}{{sqrt {{n^2} + 1} }}} right|$ $ = frac{3}{{sqrt {{n^2} + 1} }}$ $ < frac{3}{{sqrt {n_a^2 + 1} }} < a$ với $forall n > {n_a}.$
Suy ra $lim left| {frac{{1 – 2n}}{{sqrt {{n^2} + 1} }} + 2} right| = 0$ $ Rightarrow lim frac{{1 – 2n}}{{sqrt {{n^2} + 1} }} = – 2.$Ví dụ 2. Chứng minh rằng dãy số $({u_n}):{u_n} = {( – 1)^n}$ không có giới hạn.Ta có: ${u_{2n}} = 1$ $ Rightarrow lim {u_{2n}} = 1$; ${u_{2n + 1}} = – 1$ $ Rightarrow lim {u_{2n + 1}} = – 1.$
Vì giới hạn của dãy số nếu có là duy nhất nên ta suy ra dãy $left( {{u_n}} right)$ không có giới hạn.Ví dụ 3. Chứng minh các giới hạn sau:
1. $lim frac{{{n^2} + 1}}{n} = + infty .$
2. $lim frac{{2 – n}}{{sqrt n }} = – infty .$1. Với mọi số thực dương $M$ lớn tùy ý, ta có: $left| {frac{{{n^2} + 1}}{n}} right| > M$ $ Leftrightarrow {n^2} – Mn + 1 > 0$ $ Leftrightarrow n > frac{{M + sqrt {{M^2} – 4} }}{2}.$
Ta chọn ${n_0} = left[ {frac{{M + sqrt {{M^2} – 4} }}{2}} right]$ thì ta có: $frac{{{n^2} + 1}}{n} > M$, $forall n > {n_0}.$
Do đó: $lim frac{{{n^2} + 1}}{n} = + infty .$
2. Với mọi $M > 0$ lớn tùy ý, ta có: $frac{{n – 2}}{{sqrt n }} > M$ $ Leftrightarrow n – Msqrt n – 2 > 0$ $ Leftrightarrow n > {left( {frac{{M + sqrt {{M^2} + 8} }}{2}} right)^2}.$
Ta chọn ${n_0} = left[ {{{left( {frac{{M + sqrt {{M^2} + 8} }}{2}} right)}^2}} right]$ thì ta có: $frac{{n – 2}}{{sqrt n }} > M$, $forall n > {n_0}.$
Do đó: $lim frac{{2 – n}}{{sqrt n }} = – infty .$Dạng toán 2. Tìm giới hạn của dãy số dựa vào các định lý và các giới hạn cơ bản.
Phương pháp: Sử dụng các định lí về giới hạn, biến đổi đưa về các giới hạn cơ bản.
• Khi tìm $lim frac{{f(n)}}{{g(n)}}$ ta thường chia cả tử và mẫu cho ${n^k}$, trong đó $k$ là bậc lớn nhất của tử và mẫu.
• Khi tìm $lim left[ {sqrt[k]{{f(n)}} – sqrt[m]{{g(n)}}} right]$ trong đó $lim f(n) = lim g(n) = + infty $ ta thường tách và sử dụng phương pháp nhân lượng liên hợp.Ví dụ 4. Tìm các giới hạn sau:
1. $A = lim frac{{2{n^2} + 3n + 1}}{{3{n^2} – n + 2}}.$
2. $B = lim frac{{sqrt {{n^2} + n} }}{{n – sqrt {3{n^2} + 1} }}.$
3. $C = lim frac{{{{left( {2{n^2} + 1} right)}^4}{{left( {n + 2} right)}^9}}}{{{n^{17}} + 1}}.$
4. $D = lim frac{{sqrt {{n^2} + 1} – sqrt[3]{{3{n^3} + 2}}}}{{sqrt[4]{{2{n^4} + n + 2}} – n}}.$1. Ta có: $A = lim frac{{2 + frac{3}{n} + frac{1}{{{n^2}}}}}{{3 – frac{1}{n} + frac{2}{{{n^2}}}}} = frac{2}{3}.$
2. Ta có: $B = lim frac{{frac{{sqrt {{n^2} + n} }}{n}}}{{frac{{n – sqrt {3{n^2} + 1} }}{n}}}$ $ = lim frac{{sqrt {1 + frac{1}{n}} }}{{1 – sqrt {3 + frac{1}{{{n^2}}}} }}$ $ = frac{1}{{1 – sqrt 3 }}.$
3. Ta có: $C = $ $lim frac{{{n^8}{{(2 + frac{1}{{{n^2}}})}^4}.{n^9}{{(1 + frac{2}{n})}^9}}}{{{n^{17}}(1 + frac{1}{{{n^{17}}}})}}$ $ = lim frac{{{{(2 + frac{1}{{{n^2}}})}^4}.{{(1 + frac{2}{n})}^9}}}{{1 + frac{1}{{{n^{17}}}}}}$ $ = 16.$
4. Ta có: $D = $ $lim frac{{nleft( {sqrt {1 + frac{1}{{{n^2}}}} – sqrt[3]{{3 + frac{2}{{{n^3}}}}}} right)}}{{nleft( {sqrt[4]{{2 + frac{1}{{{n^3}}} + frac{2}{{{n^4}}}}} – 1} right)}}$ $ = frac{{1 – sqrt[3]{3}}}{{sqrt[4]{2} – 1}}.$Ví dụ 5. Tìm các giới hạn sau:
1. $A = lim left( {sqrt {{n^2} + 6n} – n} right).$
2. $B = lim left( {sqrt[3]{{{n^3} + 9{n^2}}} – n} right).$1. Ta có: $A = lim left( {sqrt {{n^2} + 6n} – n} right)$ $ = lim frac{{{n^2} + 6n – {n^2}}}{{sqrt {{n^2} + 6n} + n}}$ $ = lim frac{{6n}}{{sqrt {{n^2} + 6n} + n}}$ $ = lim frac{6}{{sqrt {1 + frac{6}{n}} + 1}}$ $ = 3.$
2. Ta có: $B = lim left( {sqrt[3]{{{n^3} + 9{n^2}}} – n} right)$ $ = lim frac{{9{n^2}}}{{sqrt[3]{{{{left( {{n^3} + 9{n^2}} right)}^2}}} + nsqrt[3]{{{n^3} + 9{n^2}}} + {n^2}}}$ $ = lim frac{9}{{sqrt[3]{{{{left( {1 + frac{9}{n}} right)}^2}}} + sqrt {1 + frac{9}{n}} + 1}}$ $ = 3.$Ví dụ 6. Tìm các giới hạn sau:
1. $A = lim left( {sqrt {{n^2} + 2n + 2} + n} right).$
2. $B = lim left( {sqrt {2{n^2} + 1} – n} right).$1. Ta có: $A = lim nleft( {sqrt {1 + frac{2}{n} + frac{2}{{{n^2}}}} + 1} right).$
Vì: $lim n = + infty $ và $lim left( {sqrt {1 + frac{2}{n} + frac{2}{{{n^2}}}} + 1} right) = 2 > 0.$
Nên $A = + infty .$
2. Ta có: $B = lim nleft( {sqrt {2 + frac{1}{n}} – 1} right).$
Vì: $lim n = + infty $ và $lim left( {sqrt {2 + frac{1}{n}} – 1} right)$ $ = sqrt 2 – 1 > 0.$
Nên $B = + infty .$Ví dụ 7. Tìm các giới hạn sau:
1. $A = $ $lim frac{{nsqrt {1 + 3 + 5 + … + (2n – 1)} }}{{2{n^2} + 1}}.$
2. $B = $ $lim frac{{sqrt {1 + 2 + … + n} – n}}{{sqrt[3]{{{1^2} + {2^2} + … + {n^2}}} + 2n}}.$1. Ta có: $1 + 3 + 5 + … + 2n – 1 = {n^2}.$
Suy ra $A = lim frac{{{n^2}}}{{2{n^2} + 1}}$ $ = lim frac{1}{{2 + frac{1}{{{n^2}}}}}$ $ = frac{1}{2}.$
2. Ta có:
$1 + 2 + … + n = frac{{n(n + 1)}}{2}.$
${1^2} + {2^2} + … + {n^2}$ $ = frac{{n(n + 1)(2n + 1)}}{6}.$
Suy ra: $B = $ $lim frac{{sqrt {frac{{n(n + 1)}}{2}} – n}}{{sqrt[3]{{frac{{n(n + 1)(2n + 1)}}{6}}} + 2n}}$ $ = lim frac{{sqrt {frac{{{n^2}left( {1 + frac{1}{n}} right)}}{2}} – n}}{{sqrt[3]{{frac{{{n^3}left( {1 + frac{1}{n}} right)left( {2 + frac{1}{n}} right)}}{6}}} + 2n}}$ $ = frac{{sqrt {frac{1}{2}} – 1}}{{sqrt[3]{{frac{1}{3}}} + 2}}.$Ví dụ 8. Tìm các giới hạn sau:
1. $C = $ $lim left[ {left( {1 – frac{1}{{{2^2}}}} right)left( {1 – frac{1}{{{3^2}}}} right)…left( {1 – frac{1}{{{n^2}}}} right)} right].$
2. $D = $ $lim left[ {frac{1}{{1.2}} + frac{1}{{2.3}} + frac{1}{{3.4}} + … + frac{1}{{n(n + 1)}}} right].$1. Ta có: $1 – frac{1}{{{k^2}}}$ $ = frac{{(k – 1)(k + 1)}}{{{k^2}}}$ nên suy ra:
$left( {1 – frac{1}{{{2^2}}}} right)left( {1 – frac{1}{{{3^2}}}} right)…left( {1 – frac{1}{{{n^2}}}} right)$ $ = frac{{1.3}}{{{2^2}}}.frac{{2.4}}{{{3^2}}}…frac{{(n – 1)(n + 1)}}{{{n^2}}}$ $ = frac{{n + 1}}{{2n}}.$
Do vậy $C = lim frac{{n + 1}}{{2n}} = frac{1}{2}.$
2. Ta có: $frac{1}{{k(k + 1)}}$ $ = frac{1}{k} – frac{1}{{k + 1}}$ nên suy ra $frac{1}{{1.2}} + frac{1}{{2.3}} + frac{1}{{3.4}} + … + frac{1}{{n(n + 1)}}$ $ = 1 – frac{1}{{n + 1}}.$
Vậy $D = lim left( {1 – frac{1}{{n + 1}}} right) = 1.$Ví dụ 9. Tìm các giới hạn sau:
1. $A = lim frac{{{4^{n + 1}} – {5^{n + 1}}}}{{{4^n} + {5^n}}}.$
2. $B = lim frac{{{{4.3}^{n + 2}} – {{2.7}^{n – 1}}}}{{{4^n} + {7^{n + 1}}}}.$1. Chia cả tử và mẫu cho ${5^n}$ ta có: $A = lim frac{{4{{left( {frac{4}{5}} right)}^n} – 5}}{{{{left( {frac{4}{5}} right)}^n} + 1}} = – 5$ (do $lim {left( {frac{4}{5}} right)^n} = 0$).
2. Ta có: $B = $ $lim frac{{36{{left( {frac{4}{7}} right)}^n} – frac{2}{7}}}{{{{left( {frac{4}{7}} right)}^n} + 7}}$ $ = – frac{2}{{49}}.$Ví dụ 10. Tìm giới hạn sau: $C = $ $lim left[ {left( {1 – frac{1}{{{2^2}}}} right)left( {1 – frac{1}{{{3^2}}}} right)…left( {1 – frac{1}{{{n^2}}}} right)} right].$Ta có: $1 – frac{1}{{{k^2}}}$ $ = frac{{(k – 1)(k + 1)}}{{{k^2}}}$ nên suy ra: $left( {1 – frac{1}{{{2^2}}}} right)left( {1 – frac{1}{{{3^2}}}} right)…left( {1 – frac{1}{{{n^2}}}} right)$ $ = frac{{1.3}}{{{2^2}}}.frac{{2.4}}{{{3^2}}}…frac{{(n – 1)(n + 1)}}{{{n^2}}}$ $ = frac{{n + 1}}{{2n}}.$
Do vậy $C = lim frac{{n + 1}}{{2n}} = frac{1}{2}.$
Để lại một phản hồi