Tài liệu gồm 144 trang, được biên soạn bởi thầy giáo Lê Quang Xe, tổng hợp lý thuyết cần nhớ, các dạng toán cơ bản và bài tập tự luyện chuyên đề hàm số lũy thừa, hàm số mũ và hàm số logarit, giúp học sinh lớp 12 tham khảo, rèn luyện khi học chương trình Giải tích 12 chương 2.BÀI 1. LŨY THỪA.
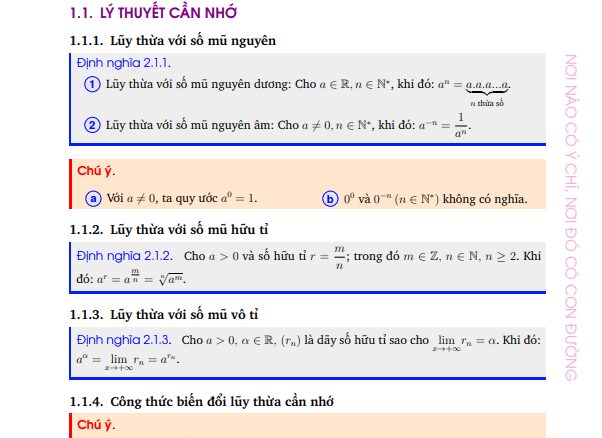
1.1. LÝ THUYẾT CẦN NHỚ.
1.1.1. Lũy thừa với số mũ nguyên.
1.1.2. Lũy thừa với số mũ hữu tỉ.
1.1.3. Lũy thừa với số mũ vô tỉ.
1.1.4. Công thức biến đổi lũy thừa cần nhớ.
1.2. CÁC DẠNG TOÁN CƠ BẢN.
Dạng 1.1. Tính giá trị biểu thức.
Dạng 1.2. Rút gọn biểu thức liên quan đến lũy thừa.
Dạng 1.3. So sánh hai lũy thừa.
1.3. BÀI TẬP TỰ LUYỆN.BÀI 2. HÀM SỐ LŨY THỪA.
2.1. LÝ THUYẾT CẦN NHỚ.
2.1.1. Khái niệm.
2.1.2. Đồ thị hàm lũy thừa.
2.2. CÁC DẠNG TOÁN CƠ BẢN.
Dạng 2.1. Tìm tập xác định của hàm số lũy thừa.
Dạng 2.2. Tìm đạo hàm của hàm số lũy thừa.
Dạng 2.3. Đồ thị của hàm số lũy thừa.
2.3. BÀI TẬP TỰ LUYỆN.BÀI 3. LÔGARIT.
3.1. LÝ THUYẾT CẦN NHỚ.
3.1.1. Định nghĩa.
3.1.2. Tính chất.
3.1.3. Các công thức lôgarit cần nhớ.
3.1.4. Lôgarít thập phân và lôgarit tự nhiên.
3.2. CÁC DẠNG TOÁN CƠ BẢN.
Dạng 3.1. So sánh hai lôgarit.
Dạng 3.2. Công thức, tính toán lôgarit.
Dạng 3.3. Phân tích biểu thức lôgarit theo các lô-ga-rit cho trước.
Dạng 3.4. Xác định một số nguyên dương có bao nhiêu chữ số.
Dạng 3.5. Tổng hợp biến đổi lôgarit nâng cao.
3.3. BÀI TẬP TỰ LUYỆN.BÀI 4. HÀM SỐ MŨ, HÀM SỐ LÔGARIT.
4.1. LÝ THUYẾT CẦN NHỚ.
4.1.1. Hàm số mũ.
4.1.2. Hàm số lôgarit.
4.1.3. Liên hệ đồ thị của hai hàm số.
4.2. CÁC DẠNG TOÁN CƠ BẢN.
Dạng 4.1. Tìm tập xác định.
Dạng 4.2. Tính đạo hàm.
Dạng 4.3. Giá trị lớn nhất và giá trị nhỏ nhất.
Dạng 4.4. Các bài toán liên quan đến đồ thị.
4.3. BÀI TẬP TỰ LUYỆN.BÀI 5. PHƯƠNG TRÌNH MŨ, PHƯƠNG TRÌNH LOGARIT CƠ BẢN.
5.1. LÝ THUYẾT CẦN NHỚ.
5.1.1. Công thức nghiệm của phương trình mũ.
5.1.2. Công thức nghiệm của phương trình lôgarit.
5.2. CÁC DẠNG TOÁN CƠ BẢN.
Dạng 5.1. cơ bản, phương pháp đưa về cùng cơ số.
Dạng 5.2. Giải phương trình mũ bằng phương pháp đặt ẩn phụ.
Dạng 5.3. Giải phương trình mũ bằng phương pháp lôgarít hóa.
Dạng 5.4. cơ bản, phương pháp đưa về cùng cơ số.
Dạng 5.5. Giải phương trình lôgarít bằng phương pháp đặt ẩn phụ.
Dạng 5.6. Giải phương trình mũ và lôgarít bằng phương pháp hàm số.
5.3. BÀI TẬP TỰ LUYỆN.BÀI 6. BẤT PHƯƠNG TRÌNH MŨ, BẤT PHƯƠNG TRÌNH LOGARIT CƠ BẢN.
6.1. LÝ THUYẾT CẦN NHỚ.
6.1.1. Công thức nghiệm của bất phương trình mũ.
6.1.2. Công thức nghiệm của bất phương trình lôgarit.
6.2. CÁC DẠNG TOÁN CƠ BẢN.
Dạng 6.1. Giải BPT mũ cơ bản, phương pháp đưa về cùng cơ số.
Dạng 6.2. bằng phương pháp đặt ẩn phụ.
Dạng 6.3. Giải BPT logarit bằng phương pháp đưa về cùng cơ số.
Dạng 6.4. bằng phương pháp đặt ẩn phụ.
Dạng 6.5. .
6.3. BÀI TẬP TỰ LUYỆN.BÀI 7. PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH MŨ, LOGARIT CÓ CHỨA THAM SỐ.
7.1. CÁC DẠNG TOÁN CƠ BẢN.
Dạng 7.1. Phương trình có nghiệm đẹp – Định lý Viét.
Dạng 7.2. Phương trình không có nghiệm đẹp – Phương pháp hàm số.
Dạng 7.3. Bất phương trình – Phương pháp hàm số.
7.2. BÀI TẬP TỰ LUYỆN.

Be the first to comment