
Bài viết trình bày một số ứng dụng của định lí Vi-ét trong việc giải các bài toán liên quan đến tam thức bậc hai và phương trình trình bậc hai.A. ĐỊNH LÍ VI-ÉT VÀ ỨNG DỤNG
1. Định lí Vi-ét đối với phương trình bậc hai: Hai số ${{x}_{1}}$ và ${{x}_{2}}$ là các nghiệm của phương trình bậc hai $a{{x}^{2}}+bx+c=0$ khi và chỉ khi chúng thỏa mãn hệ thức ${{x}_{1}}+{{x}_{2}}=-frac{b}{a}$ và ${{x}_{1}}{{x}_{2}}=frac{c}{a}.$
2. Ứng dụng của định lí Vi-ét
Một số ứng dụng của định lí Vi-ét:
• Nhẩm nghiệm của phương trình bậc hai.
• Phân tích đa thức thành nhân tử: Nếu đa thức $fleft( x right)=a{{x}^{2}}+bx+c$ có hai nghiệm ${{x}_{1}}$ và ${{x}_{2}}$ thì nó có thể phân tích thành nhân tử $fleft( x right)=aleft( x-{{x}_{1}} right)left( x-{{x}_{2}} right)$.
• Tìm hai số khi biết tổng và tích của chúng: Nếu hai số có tổng là $text{S}$ và tích là $P$ thì chúng là nghiệm của phương trình ${{x}^{2}}-Sx+P=0$.
• Xét dấu của các nghiệm phương trình bậc hai:
Cho phương trình bậc hai $a{{x}^{2}}+bx+c=0$ $(*)$, kí hiệu $text{S}=-frac{b}{a}$, $P=frac{c}{a}$ khi đó:
+ Phương trình $(*)$ có hai nghiệm trái dấu khi và chỉ khi $P<0.$
+ Phương trình $(*)$ có hai nghiệm dương khi và chỉ khi $left{ begin{matrix}
Delta ge 0 \
begin{align}
& P>0 \
& S>0 \
end{align} \
end{matrix} right.$
+ Phương trình $(*)$ có hai nghiệm âm khi và chỉ khi $left{ begin{matrix}
Delta ge 0 \
begin{align}
& P>0 \
& S<0 \
end{align} \
end{matrix} right.$B. CÁC DẠNG TOÁN ỨNG DỤNG ĐỊNH LÍ VI-ÉT
Dạng toán 1. Nhẩm nghiệm phương trình bậc hai.
Ví dụ 1. Cho phương trình $2{{x}^{2}}-mx+5=0$. Biết phương trình có một nghiệm là $2$. Tìm $m$ và tìm nghiệm còn lại.Cách 1: Vì phương trình có nghiệm nên theo hệ thức Vi-ét ta có ${{x}_{1}}{{x}_{2}}=frac{5}{2}.$
Giả sử ${{x}_{1}}=2$ suy ra ${{x}_{2}}=frac{5}{4}.$
Mặt khác ${{x}_{1}}+{{x}_{2}}=frac{m}{2}$ $Rightarrow 2+frac{5}{4}=frac{m}{2}$ $Rightarrow m=frac{13}{2}$.
Vậy $m=frac{13}{2}$ và nghiệm còn lại là $frac{5}{2}.$
Cách 2. Thay $x=2$ vào phương trình ta được $8-2m+5=0$ $Leftrightarrow m=frac{13}{2}.$
Theo hệ thức Vi-ét ta có ${{x}_{1}}{{x}_{2}}=frac{5}{2}$ mà ${{x}_{1}}=2$ nên ${{x}_{2}}=frac{5}{4}.$
Vậy $m=frac{13}{2}$ và nghiệm còn lại là $frac{5}{2}.$Dạng toán 2. Phân tích đa thức thành nhân tử.
Ví dụ 2. Phân tích đa thức sau thành nhân tử:
a) $f(x)=3{{x}^{2}}-14x+8.$
b) $g(x)=-{{x}^{4}}+5{{x}^{2}}-4.$
c) $P(x;y)=6{{x}^{2}}-11xy+3{{y}^{2}}.$
d) $Q(x;y)=2{{x}^{2}}-2{{y}^{2}}-3xy+x-2y.$a) Phương trình $3{{x}^{2}}-14x+8=0$ $Leftrightarrow left[ begin{matrix}
x=frac{2}{3} \
x=4 \
end{matrix} right.$
Suy ra $f(x)=3left( x-frac{2}{3} right)left( x-4 right)$ $=left( 3x-2 right)left( x-4 right).$
b) Phương trình $-{{x}^{4}}+5{{x}^{2}}-4=0$ $Leftrightarrow -{{left( {{x}^{2}} right)}^{2}}+5{{x}^{2}}-4=0$ $Leftrightarrow left[ begin{matrix}
{{x}^{2}}=1 \
{{x}^{2}}=4 \
end{matrix} right.$
Suy ra $g(x)=-left( {{x}^{2}}-1 right)left( {{x}^{2}}-4 right)$ $=-left( x-1 right)left( x+1 right)left( x-2 right)left( x+2 right).$
c) Xét phương trình $6{{x}^{2}}-11xy+3{{y}^{2}}=0$ ẩn $x.$
Ta có: ${{Delta }_{x}}={{left( 11y right)}^{2}}-4.18{{y}^{2}}=49{{y}^{2}}.$
Suy ra phương trình có nghiệm là $x=frac{11ypm 7y}{12}$ $Leftrightarrow left[ begin{matrix}
x=frac{y}{3} \
x=frac{3y}{2} \
end{matrix} right.$
Do đó $P(x;y)=6left( x-frac{y}{3} right)left( x-frac{3y}{2} right)$ $=left( 3x-y right)left( 2x-3y right).$
d) Xét phương trình ẩn $x$ sau: $2{{x}^{2}}-2{{y}^{2}}-3xy+x-2y=0$ $Leftrightarrow 2{{x}^{2}}+left( 1-3y right)x-2{{y}^{2}}-2y=0.$
Ta có: ${{Delta }_{x}}={{left( 1-3y right)}^{2}}-8left( -2{{y}^{2}}-2y right)$ $=25{{y}^{2}}+10y+1$ $={{left( 5y+1 right)}^{2}}.$
Suy ra phương trình có nghiệm là $x=frac{3y-1pm left( 5y+1 right)}{4}$ $Leftrightarrow left[ begin{matrix}
x=2y \
x=frac{-y-1}{2} \
end{matrix} right.$
Do đó $Q(x;y)=2left( x-2y right)left( x-frac{-y-1}{2} right)$ $=left( x-2y right)left( 2x+y+1 right).$Ví dụ 3. Phân tích đa thức $fleft( x right)={{x}^{4}}-2m{{x}^{2}}-x+{{m}^{2}}-m$ thành tích của hai tam thức bậc hai ẩn $x.$Ta có $fleft( x right)=0$ $Leftrightarrow {{x}^{4}}-2m{{x}^{2}}-x+{{m}^{2}}-m=0$ $Leftrightarrow {{m}^{2}}-left( 2{{x}^{2}}+1 right)m+{{x}^{4}}-x=0.$
${{Delta }_{m}}={{left( 2{{x}^{2}}+1 right)}^{2}}-4left( {{x}^{4}}-x right)$ $=4{{x}^{2}}+4x+1={{left( 2x+1 right)}^{2}}.$
Suy ra $fleft( x right)=0$ $Leftrightarrow left[ begin{matrix}
m=frac{2{{x}^{2}}+1+2x+1}{2}={{x}^{2}}+x+1 \
m=frac{2{{x}^{2}}+1-2x-1}{2}={{x}^{2}}-x \
end{matrix} right.$
Vậy $fleft( x right)=left( m-{{x}^{2}}-x-1 right)left( m-{{x}^{2}}+x right).$
[ads]
Dạng toán 3. Bài toán liên quan đến biểu thức đối xứng hai nghiệm ${{x}_{1}}$, ${{x}_{2}}$ của phương trình bậc hai.
Ví dụ 4. Cho phương trình ${{x}^{2}}-2left( m+1 right)x+{{m}^{2}}+2=0$ với $m$là tham số. Tìm $m$ để phương trình có hai nghiệm ${{x}_{1}}$,${{x}_{2}}$ sao cho:
a) $x_{1}^{3}+x_{2}^{3}=2{{x}_{1}}{{x}_{2}}left( {{x}_{1}}+{{x}_{2}} right).$
b) $left| x_{1}^{4}-x_{2}^{4} right|=16{{m}^{2}}+64m.$
c) $A={{x}_{1}}{{x}_{2}}-2left( {{x}_{1}}+{{x}_{2}} right)-6$ đạt giá trị nhỏ nhất.
d) $B=sqrt{2left( x_{1}^{2}+x_{2}^{2} right)+16}-3{{x}_{1}}{{x}_{2}}$ đạt giá trị lớn nhất.Ta có phương trình có hai nghiệm ${{x}_{1}}$, ${{x}_{2}}$ khi và chỉ khi $Delta’ge 0$ $Leftrightarrow {{left( m+1 right)}^{2}}-left( {{m}^{2}}+2 right)ge 0$ $Leftrightarrow mge frac{1}{2}.$
Theo định lí Vi-ét ta có: $left{ begin{matrix}
{{x}_{1}}+{{x}_{2}}=2m+2 \
{{x}_{1}}.{{x}_{2}}={{m}^{2}}+2 \
end{matrix} right.$
a) Ta có $x_{1}^{3}+x_{2}^{3}$ $={{left( {{x}_{1}}+{{x}_{2}} right)}^{3}}-3{{x}_{1}}{{x}_{2}}left( {{x}_{1}}+{{x}_{2}} right).$
Suy ra $x_{1}^{3}+x_{2}^{3}=2{{x}_{1}}{{x}_{2}}left( {{x}_{1}}+{{x}_{2}} right)$ $Leftrightarrow {{left( {{x}_{1}}+{{x}_{2}} right)}^{3}}-3{{x}_{1}}{{x}_{2}}left( {{x}_{1}}+{{x}_{2}} right)$ $=2{{x}_{1}}{{x}_{2}}left( {{x}_{1}}+{{x}_{2}} right)$ $Leftrightarrow left( {{x}_{1}}+{{x}_{2}} right)left[ {{left( {{x}_{1}}+{{x}_{2}} right)}^{2}}-5{{x}_{1}}{{x}_{2}} right]=0.$
Suy ra $left( 2m+2 right)left[ {{left( 2m+2 right)}^{2}}-5left( {{m}^{2}}+2 right) right]=0$ $Leftrightarrow 2left( m+1 right)left( -{{m}^{2}}+8m-6 right)=0$ $ Leftrightarrow left[ {begin{array}{*{20}{c}}
{m + 1 = 0}\
{ – {m^2} + 8m – 6 = 0}
end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{c}}
{m = – 1}\
{m = 4 pm sqrt {10} }
end{array}} right.$
Đối chiếu với điều kiện $m ge frac{1}{2}$ ta thấy chỉ có $m=4pm sqrt{10}$ thỏa mãn.
Vậy $m=4pm sqrt{10}$ thỏa mãn yêu cầu bài toán.
b) Ta có $left| x_{1}^{4}-x_{2}^{4} right|$ $=left| left( x_{1}^{2}+x_{2}^{2} right)left( x_{1}^{2}-x_{2}^{2} right) right|$ $=left[ {{left( {{x}_{1}}+{{x}_{2}} right)}^{2}}-2{{x}_{1}}{{x}_{2}} right]left| {{x}_{1}}-{{x}_{2}} right|left| {{x}_{1}}+{{x}_{2}} right|.$
Mà: $left| {{x}_{1}}-{{x}_{2}} right|$ $=sqrt{{{left( {{x}_{1}}-{{x}_{2}} right)}^{2}}}$ $=sqrt{{{left( {{x}_{1}}+{{x}_{2}} right)}^{2}}-4{{x}_{1}}{{x}_{2}}}$ $=sqrt{{{left( 2m+2 right)}^{2}}-4left( {{m}^{2}}+2 right)}$ $=sqrt{8m-4}.$
Suy ra: $left| x_{1}^{4}-x_{2}^{4} right|$ $=left[ {{left( 2m+2 right)}^{2}}-2left( {{m}^{2}}+2 right) right]$$sqrt{8m-4}left| 2m+2 right|$ $=left( 2{{m}^{2}}+8m right)sqrt{8m-4}left| 2m+2 right|.$
Suy ra $left| x_{1}^{4}-x_{2}^{4} right|$ $=16{{m}^{2}}+64m$ $Leftrightarrow left( 2{{m}^{2}}+8m right)sqrt{8m-4}left| 2m+2 right|$ $=16{{m}^{2}}+64m$ $ Leftrightarrow left( {{m^2} + 4m} right)left( {sqrt {8m – 4} left| {2m + 2} right| – 8} right) = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{c}}
{{m^2} + 4m = 0:(1)}\
{sqrt {8m – 4} left| {2m + 2} right| = 8:(2)}
end{array}} right.$
Ta có:
$left( 1 right)$ $Leftrightarrow left[ begin{matrix}
m=0 \
m=-4 \
end{matrix} right.$ (loại).
$left( 2 right)$ $Leftrightarrow left( 8m-4 right){{left( 2m+2 right)}^{2}}=64$ $Leftrightarrow 32{{m}^{3}}+48{{m}^{2}}-80=0$ $Leftrightarrow m=1$ (thỏa mãn điều kiện $m ge frac{1}{2}$).
Vậy $m=1$ thỏa mãn yêu cầu bài toán.
c) Ta có $A={{x}_{1}}{{x}_{2}}-2left( {{x}_{1}}+{{x}_{2}} right)-6$ $={{m}^{2}}+2-2left( 2m+2 right)-6$ $={{m}^{2}}-4m-8.$
$Rightarrow A={{left( m-2 right)}^{2}}-12ge -12.$
Suy ra $min A=-12$ $Leftrightarrow m=2$ (thỏa mãn điều kiện $m ge frac{1}{2}$).
Vậy với $m=2$ thì biểu thức $A$ đạt giá trị nhỏ nhất.
d) Ta có: $B=sqrt{2left( x_{1}^{2}+x_{2}^{2} right)+16}-3{{x}_{1}}{{x}_{2}}$ $=sqrt{2{{left( {{x}_{1}}+{{x}_{2}} right)}^{2}}-4{{x}_{1}}{{x}_{2}}+16}-3{{x}_{1}}{{x}_{2}}$ $=sqrt{2{{left( 2m+2 right)}^{2}}-4left( {{m}^{2}}+2 right)+16}-3left( {{m}^{2}}+2 right)$ $=sqrt{4{{m}^{2}}+16m+16}-3left( {{m}^{2}}+2 right)$ $=2m+4-3left( {{m}^{2}}+2 right)$ $=-3{{m}^{2}}+2m-2.$
Xét hàm số $y=-3{{m}^{2}}+2m-2$ với $mge frac{1}{2}.$
Bảng biến thiên: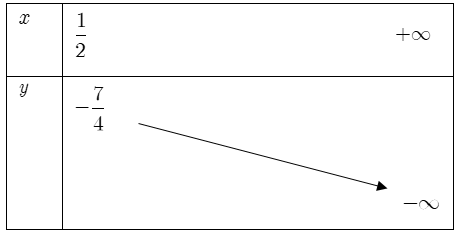 Suy ra giá trị $underset{mge frac{1}{2}}{mathop{max y}}=-frac{7}{4}$ khi $m=frac{1}{2}.$
Suy ra giá trị $underset{mge frac{1}{2}}{mathop{max y}}=-frac{7}{4}$ khi $m=frac{1}{2}.$
Vậy giá trị lớn nhất của biểu thức $B$ là $-frac{7}{4}$ khi $m=frac{1}{2}.$Ví dụ 5. Cho phương trình ${{x}^{2}}-mx+m-1=0$ với $m$ là tham số.
a) Chứng minh rằng phương trình luôn có nghiệm với mọi $m.$
b) Gọi ${{x}_{1}}$, ${{x}_{2}}$ là hai nghiệm của phương trình. Tìm hệ thức liên hệ giữa ${{x}_{1}}$, ${{x}_{2}}$ không phụ thuộc vào $m.$
c) Tìm giá trị nhỏ nhất và lớn nhất của biểu thức $A=frac{2{{x}_{1}}{{x}_{2}}+3}{x_{1}^{2}+x_{2}^{2}+2({{x}_{1}}{{x}_{2}}+1)}.$a) Ta có $Delta ={{m}^{2}}-4left( m-1 right)$ $={{left( m-2 right)}^{2}}~ge 0$ nên phương trình có nghiệm với mọi giá trị của $m.$
b) Theo hệ thức Vi-ét ta có: ${{x}_{1}}+{{x}_{2}}=m$ và ${{x}_{1}}{{x}_{2}}=m-1.$
Suy ra hệ thức liên hệ giữa ${{x}_{1}}$, ${{x}_{2}}$ không phụ thuộc vào $m$ là ${{x}_{1}}{{x}_{2}}={{x}_{1}}+{{x}_{2}}-1.$
c) Ta có $x_{1}^{2}+x_{2}^{2}$ $={{left( {{x}_{1}}+{{x}_{2}} right)}^{2}}-2{{x}_{1}}{{x}_{2}}$ $={{m}^{2}}-2m+2.$
Suy ra $A=frac{2{{x}_{1}}{{x}_{2}}+3}{x_{1}^{2}+x_{2}^{2}+2({{x}_{1}}{{x}_{2}}+1)}$ $=frac{2m+1}{{{m}^{2}}+2}.$
Vì $A-1=frac{2m+1}{{{m}^{2}}+2}-1$ $=frac{2m+1-{{m}^{2}}-2}{{{m}^{2}}+2}$ $=-frac{{{left( m-1 right)}^{2}}}{{{m}^{2}}+2}le 0$, $forall m$ $Rightarrow Ale 1$, $forall m.$
Dấu bằng xảy ra khi và chỉ khi $m=1.$
Và $A+frac{1}{2}$ $=frac{2m+1}{{{m}^{2}}+2}+frac{1}{2}$ $=frac{2left( 2m+1 right)+{{m}^{2}}+2}{2left( {{m}^{2}}+2 right)}$ $=frac{{{left( m+2 right)}^{2}}}{2left( {{m}^{2}}+2 right)}ge 0$, $forall m$ $Rightarrow Age -frac{1}{2}$, $forall m.$
Dấu bằng xảy ra khi và chỉ khi $m=-2.$
Vậy $max A=1$ khi và chỉ khi $m=1$, $min A=-frac{1}{2}$ khi và chỉ khi $m=-2.$C. BÀI TẬP RÈN LUYỆN
1. Đề bài
Bài toán 1. Phân tích đa thức sau thành nhân tử:
a) $f(x)=2{{x}^{2}}-5x+3.$
b) $g(x)=2{{x}^{4}}-14{{x}^{2}}-36.$
c) $P(x;y)=3{{x}^{2}}-5xy-2{{y}^{2}}.$
d) $Q(x;y)={{x}^{2}}-2{{y}^{2}}-xy-3y-1.$Bài toán 2. Phân tích đa thức $fleft( x right)=2{{x}^{3}}+left( m+1 right){{x}^{2}}+2mx+{{m}^{2}}+m$ (biến $x$ và tham số $m$) thành tích một đa thức bậc hai và một đa thức bậc nhất.Bài toán 3. Gọi ${{x}_{1}}$, ${{x}_{2}}$ là hai nghiệm của phương trình: $-{{x}^{2}}+3x+1=0$. Tính giá trị của các biểu thức:
$A=x_{1}^{2}+x_{2}^{2}.$
$B=x_{1}^{3}left( {{x}_{1}}-1 right)+x_{2}^{3}left( {{x}_{2}}-1 right).$
$C=left| frac{1}{x_{1}^{2}}-frac{1}{x_{2}^{2}} right|.$Bài toán 4. Tìm $m$ để phương trình $3{{x}^{2}}+4left( m-1 right)x+{{m}^{2}}-4m+1=0$ có hai nghiệm phân biệt ${{x}_{1}}$, ${{x}_{2}}$ thỏa mãn: $frac{1}{{{x}_{1}}}+frac{1}{{{x}_{2}}}=frac{1}{2}left( {{x}_{1}}+{{x}_{2}} right).$Bài toán 5. Cho phương trình ${{x}^{2}}-2left( m-1 right)x+{{m}^{2}}-3=0$ với $m$ là tham số. Tìm $m$ để phương trình có hai nghiệm ${{x}_{1}}$; ${{x}_{2}}$ sao cho:
a) ${{x}_{1}}+{{x}_{2}}=2{{x}_{1}}{{x}_{2}}.$
b) $A=2left( x_{1}^{2}+x_{2}^{2} right)-{{x}_{1}}{{x}_{2}}$ đạt giá trị lớn nhất.
c) $B=frac{{{x}_{1}}{{x}_{2}}}{x_{1}^{2}+x_{2}^{2}-{{x}_{1}}{{x}_{2}}}$ đạt giá trị nhỏ nhất.2. Hướng dẫn giải và đáp số
Bài toán 1.
a) Phương trình $2{{x}^{2}}-5x+3=0$ $Leftrightarrow left[ begin{matrix}
x=frac{3}{2} \
x=1 \
end{matrix} right.$
Suy ra $f(x)=left( 2x-3 right)left( x-1 right).$
b) $g(x)=2left( {{x}^{2}}+2 right)left( {{x}^{2}}-9 right)$ $=2left( {{x}^{2}}+2 right)left( x-3 right)left( x+3 right).$
c) $P(x;y)=left( x-2y right)left( 3x+y right).$
d) $Q(x;y)=left( x-2y-1 right)left( x+y+1 right).$Bài toán 2. $fleft( x right) = ({x^2} + m)(2x + m + 1).$Bài toán 3. Ta có $Delta ={{3}^{2}}+4=13>0$ nên phương trình đã cho luôn có hai nghiệm phân biệt ${{x}_{1}}$, ${{x}_{2}}.$
Theo định lí Vi-ét ta có: ${{x}_{1}}+{{x}_{2}}=3$, ${{x}_{1}}{{x}_{2}}=-1.$
Khi đó: $A=11$, $B=83$, $C=3sqrt{13}.$Bài toán 4.
Trước hết phương trình phải có hai nghiệm khác $0$ nên: $left{ begin{align}
& Delta’={{m}^{2}}+4m+1>0 \
& frac{c}{a}=frac{{{m}^{2}}-4m+1}{3}ne 0 \
end{align} right.$ $Leftrightarrow left{ begin{align}
& {{m}^{2}}+4m+1>0 \
& {{m}^{2}}-4m+1ne 0 \
end{align} right.$ $(*).$
Khi đó theo định lí Vi-ét ta có: ${{x}_{1}}+{{x}_{2}}=frac{4left( 1-m right)}{3}$, ${{x}_{1}}{{x}_{2}}=frac{{{m}^{2}}-4m+1}{3}.$
Ta có: $frac{1}{{{x}_{1}}}+frac{1}{{{x}_{2}}}=frac{1}{2}left( {{x}_{1}}+{{x}_{2}} right)$ $Leftrightarrow left( {{x}_{1}}+{{x}_{2}} right)left( {{x}_{1}}{{x}_{2}}-2 right)=0$ (vì ${{x}_{1}}{{x}_{2}}ne 0$) $Leftrightarrow left[ begin{align}
& {{x}_{1}}+{{x}_{2}}=0 \
& {{x}_{1}}{{x}_{2}}-2=0 \
end{align} right.$ $Leftrightarrow left[ begin{align}
& m=1 \
& {{m}^{2}}-4m-5=0 \
end{align} right.$ $Leftrightarrow m=1$, $m=-1$, $m=5.$
Thay vào $(*)$ ta thấy $m=-1$ không thỏa mãn.
Vậy $m=1$, $m=5$ là giá trị cần tìm.Bài toán 5. Ta có phương trình có hai nghiệm ${{x}_{1}}$, ${{x}_{2}}$ khi và chỉ khi $Delta’ge 0$ $Leftrightarrow {{left( m-1 right)}^{2}}-left( {{m}^{2}}-3 right)ge 0$ $Leftrightarrow mle 2.$
Theo định lí Vi-ét ta có: $left{ begin{matrix}
{{x}_{1}}+{{x}_{2}}=2m-2 \
{{x}_{1}}.{{x}_{2}}={{m}^{2}}-3 \
end{matrix} right.$
a) ${{x}_{1}}+{{x}_{2}}=2{{x}_{1}}{{x}_{2}}$ $Leftrightarrow 2m-2=2left( {{m}^{2}}-3 right)$ $Leftrightarrow left[ begin{matrix}
m=-1 \
m=2 \
end{matrix} right.$ (thỏa mãn điều kiện $mle 2$).
b) $A=2{{left( {{x}_{1}}+{{x}_{2}} right)}^{2}}-5{{x}_{1}}{{x}_{2}}$ $=2left( 2m-2 right)-5left( {{m}^{2}}-3 right)$ $=-5{{m}^{2}}+4m+11$ $=-5{{left( m-frac{2}{5} right)}^{2}}+3le 3.$
Đẳng thức xảy ra khi và chỉ khi $m=frac{2}{5}.$
c) $B=frac{{{x}_{1}}{{x}_{2}}}{{{left( {{x}_{1}}+{{x}_{2}} right)}^{2}}-3{{x}_{1}}{{x}_{2}}}$ $=frac{{{m}^{2}}-3}{{{left( 2m-2 right)}^{2}}-3left( {{m}^{2}}-3 right)}$ $=frac{{{m}^{2}}-3}{{{m}^{2}}-8m+13}.$
Suy ra $min B=-frac{1}{3}$ khi và chỉ khi $m=1.$

Be the first to comment