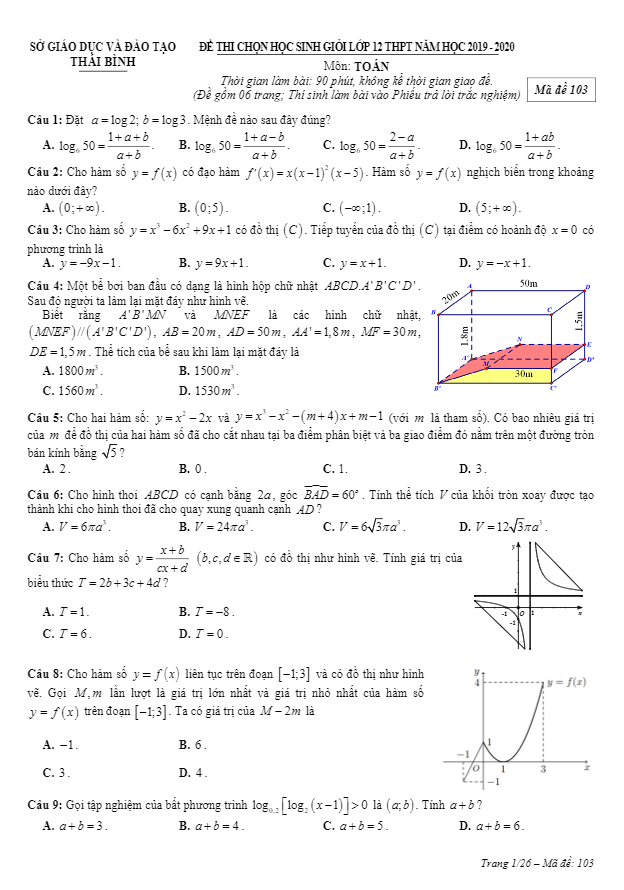
Vừa qua, sở Giáo dục và Đào tạo tỉnh Thái Bình đã tổ chức kỳ thi chọn học sinh giỏi (HSG) môn Toán lớp 12 THPT năm học 2019 – 2020.Đề chọn học sinh giỏi Toán 12 THPT năm 2019 – 2020 sở GD&ĐT Thái Bình với 4 mã đề: 103, 203, 303, 403; đề được biên soạn theo dạng trắc nghiệm với 50 câu, thời gian làm bài 90 phút, không kể thời gian giao đề, đề gồm 06 trang, thí sinh làm bài vào phiếu trả lời trắc nghiệm, đề thi có đáp án.Trích dẫn đề chọn học sinh giỏi Toán 12 THPT năm 2019 – 2020 sở GD&ĐT Thái Bình:
+ Một bể bơi ban đầu có dạng là hình hộp chữ nhật ABCD.A’B’C’D’. Sau đó người ta làm lại mặt đáy như hình vẽ. Biết rằng A’B’MN và MNEF là các hình chữ nhật, (MNEF // A’B’C’D’), AB = 20m, AD = 50m, AA’ = 1,8m, MF = 30m, DE = 1,5m. Thể tích của bể sau khi làm lại mặt đáy là?
+ Cho hai hàm số: y = x^2 – 2x và y = x^3 – x^2 – (m + 4)x + m – 1 (với m là tham số). Có bao nhiêu giá trị của m để đồ thị của hai hàm số đã cho cắt nhau tại ba điểm phân biệt và ba giao điểm đó nằm trên một đường tròn bán kính bằng √5?
[ads]
+ Cho tam giác ABC vuông tại A, AB = 6cm, AC = 3cm. M là một điểm di động trên cạnh BC (M khác B và C); gọi H, K lần lượt là hình chiếu vuông góc của M trên AB và AC. Cho hình chữ nhật AHMK quay xung quanh cạnh AH, khối trụ được tạo thành có thể tích lớn nhất là?
+ Gọi S là tập hợp các số tự nhiên có 6 chữ số đôi một khác nhau. Lấy ngẫu nhiên một số thuộc tập S. Tính xác suất để số lấy được có chữ số đứng sau lớn hơn chữ số đứng liền trước.
+ Cho hàm số y = x^3 – 3x^2 – mx + m^2 – 10 (m là tham số). Có bao nhiêu giá trị của m để đồ thị hàm số cắt trục Ox tại ba điểm phân biệt có hoành độ lập thành cấp số cộng?

Be the first to comment