Tài liệu gồm 65 trang, được biên soạn bởi quý thầy, cô giáo nhóm Strong Team Toán VD – VDC, tuyển chọn 58 bài tập trắc nghiệm tìm số nghiệm của phương trình hàm hợp có đáp án và lời giải chi tiết, đây là dạng toán vận dụng – vận dụng cao (VD – VDC) thường gặp trong chương trình Giải tích 12 chương 1 và các đề thi tốt nghiệp THPT Quốc gia môn Toán.Trích dẫn tài liệu bài tập trắc nghiệm tìm số nghiệm của phương trình hàm hợp:
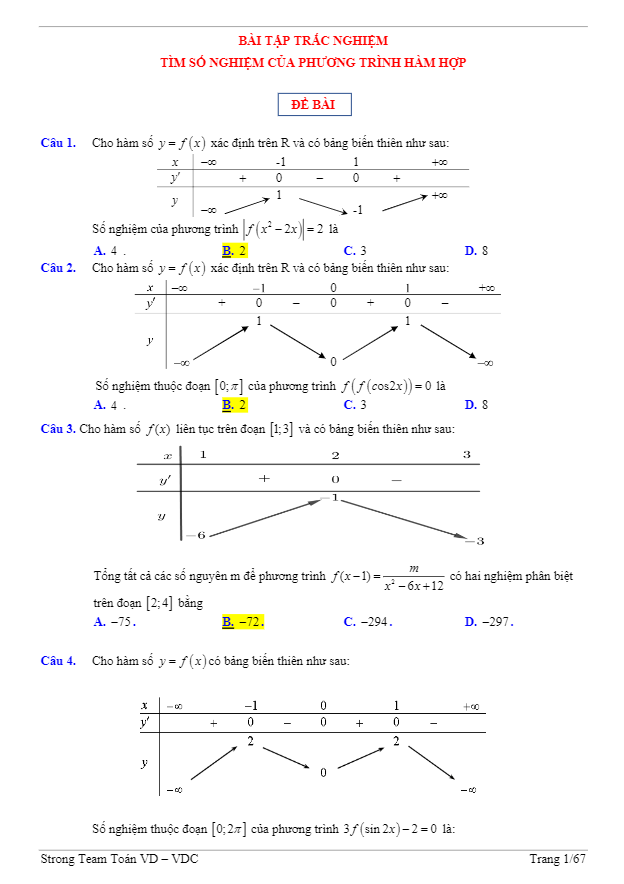
+ Cho hàm số f(x) liên tục trên đoạn [1;3] và có bảng biến thiên như sau. Tổng tất cả các số nguyên m để phương trình f(x – 1) = m/(x^2 – 6x + 12) có hai nghiệm phân biệt trên đoạn [2;4] bằng?
+ Cho hàm số y = f(x) có đồ thị như hình vẽ và lim y = -vc khi x -> ±vc. Hỏi có bao nhiêu điểm trên đường tròn lượng giác biểu diễn nghiệm của phương trình f(f(cos 2x)) = 0?
+ Cho hàm số liên tục trên có đồ thị như hình vẽ bên. Phương trình f(3 – 2f(x)) = 1 có tất cả bao nhiêu nghiệm thực phân biệt?
+ Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(sin x) = 2sin x + 2m có nghiệm thuộc khoảng (0;pi). Tổng các phần tử của S bằng?
+ Cho hàm số y = f(x) có đồ thị như hình bên. Tồn tại bao nhiêu giá trị nguyên của tham số m để phương trình f(sin x) = m có đúng hai nghiệm thuộc đoạn [0;pi]?
[ads]
Xem thêm:
+
+

Be the first to comment