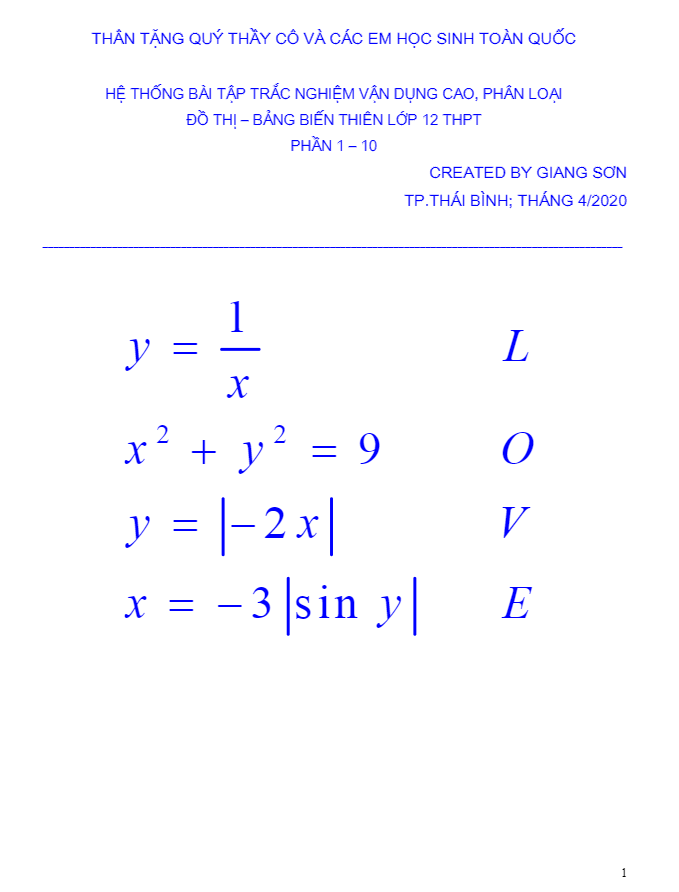
Tài liệu gồm 21 trang được biên soạn bởi thầy Lương Tuấn Đức (Giang Sơn), tuyển tập hệ thống bài tập trắc nghiệm vận dụng cao, phân loại đồ thị – bảng biến thiên (phần 1 – 10) thuộc chương trình Giải tích 12, giúp học sinh ôn tập chuẩn bị cho kỳ thi THPT Quốc gia môn Toán.Trích dẫn tài liệu hệ thống bài tập trắc nghiệm vận dụng cao, phân loại đồ thị – bảng biến thiên (phần 1 – 10):
+ Cho hàm số y = f(x) liên tục trên [0;5,5], đồ thị của hàm số trên [0;5,5] như hình vẽ. Hỏi hàm số g = [f(x)]^2 có tối đa bao nhiêu điểm cực trị?
+ Cho hàm số y = 2019x^2019 + 2017x^2017 + … + 3x^3 + 1999x – 1993|x – 1| + 1992. Có bao nhiêu giá trị nguyên không âm của m để phương trình f(3sin2x + 8(cosx)^2 – 4) = f(m^2 + m) có nghiệm thực?
+ Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Số các giá trị nguyên của tham số m không vượt quá 5 để phương trình f(pi^x) – (m^2 – 1)/8 = 0 có hai nghiệm phân biệt là?
[ads]
+ Hàm số y = e^-2x^2 có đồ thị như hình vẽ bên. ABCD là hình chữ nhật thay đổi sao cho A và B luôn thuộc đồ thị hàm số đã cho. CD luôn nằm trên trục hoành. Giá trị lớn nhất của diện tích hình chữ nhật ABCD là?
+ Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên m để phương trình f(6sinx + 8cosx) = f(m(m + 1)) có nghiệm thực?Xem thêm:

Be the first to comment