Tài liệu gồm 21 trang được biên soạn bởi thầy giáo Lương Tuấn Đức (Facebook: Giang Sơn) tuyển tập hệ thống bài tập trắc nghiệm vận dụng cao, phân loại đồ thị đạo hàm – bảng biến thiên (phần 1 đến phần 10), giúp học sinh học nâng cao chương trình Giải tích 12 chương 1 và ôn thi THPT Quốc gia môn Toán.Trích dẫn tài liệu hệ thống bài tập trắc nghiệm vận dụng cao, phân loại đồ thị đạo hàm – bảng biến thiên (phần 1 – 10):
+ Cho hàm số bậc ba y = f(x). Hàm số y = f'(x) có đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y = f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương. Hỏi đồ thị hàm số y = f(x) cắt trục tung tại điểm có tung độ bằng bao nhiêu?
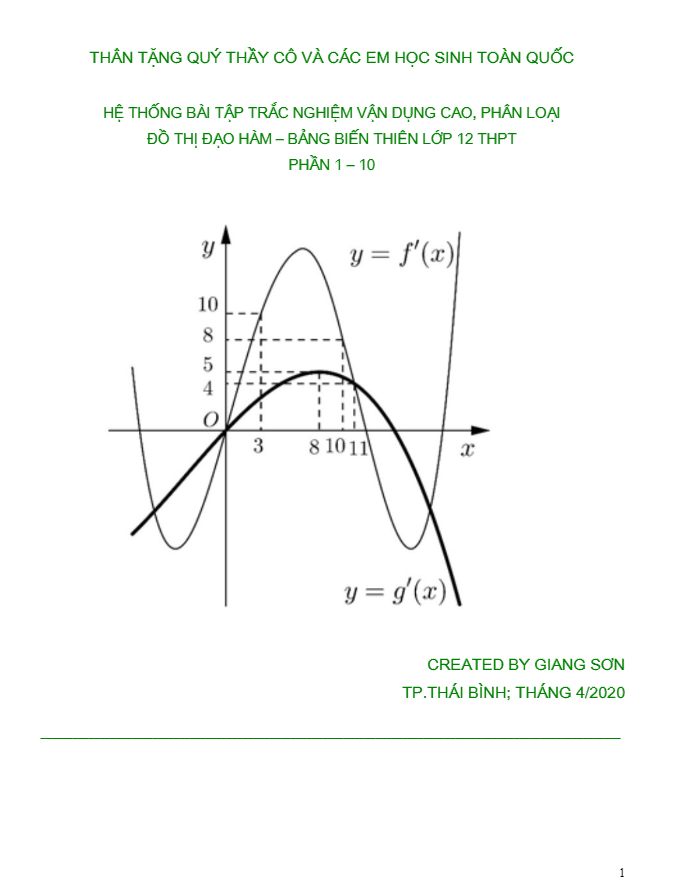
+ Cho hai hàm số y = f(x) và y = g(x). Hai hàm số y = f'(x) và y = g'(x) có đồ thị như hình vẽ bên. Biết rằng f(0) – f(6) < g(0) – g(6). Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h(x) = f(x) – g(x) trên đoạn [0;6] lần lượt là?
[ads]
+ Trên đoạn [–1;3] hàm số y = f(x) liên tục và thỏa mãn f(-1) = m^2. Hàm số y = f'(x) trên miền [–1;3] có đồ thị như hình vẽ bên. Tồn tại bao nhiêu số nguyên m thuộc đoạn [–1993;1993] để bất phương trình nghiệm đúng với mọi giá trị x thuộc [-1;3].
+ Cho hàm số y = f(x) liên tục trên R và có đồ thị đi qua điểm hai điểm A(1;0), B(3;2). Hàm số y = f'(x) có đồ thị như hình vẽ bên. Tồn tại bao nhiêu số nguyên dương m nhỏ hơn 50 để bất phương trình sau nghiệm đúng với mọi x thuộc [0;3].
+ Cho hàm số y = f(x). Giả sử hàm số y = f'(x) có đồ thị như hình vẽ bên. Hàm số g = f(x^2 + 4x + 3) có bao nhiêu điểm cực tiểu?Xem thêm:

Be the first to comment