
Bài viết hướng dẫn phương pháp tính tích phân hàm chứa giá trị tuyệt đối, đây là dạng toán thường gặp trong chương trình Giải tích 12 chương 3.1. Phương pháp tính tích phân hàm chứa giá trị tuyệt đối
Muốn tính tích phân $I = int_a^b | f(x)|dx$, ta thức hiện theo các bước sau:
+ Xét dấu hàm $f(x)$ trên đoạn $[a;b]$ để mở dấu giá trị tuyệt đối.
+ Áp dụng công thức: $int_a^b | f(x)|dx$ $ = int_a^c | f(x)|dx + int_c^b | f(x)|dx.$
2. Một số ví dụ minh họaVí dụ 1: Tính tích phân: $I = int_{ – 3}^3 {left| {{x^2} – 1} right|} dx.$Ta có: $I = int_{ – 3}^3 {left| {{x^2} – 1} right|} dx$ $ = int_{ – 3}^{ – 1} {left( {{x^2} – 1} right)} dx$ $ + int_{ – 1}^1 {left( { – {x^2} + 1} right)} dx$ $ + int_1^3 {left( {{x^2} – 1} right)} dx$ $ = left. {left( {frac{{{x^3}}}{3} – x} right)} right|_{ – 3}^{ – 1}$ $ + left. {left( { – frac{{{x^3}}}{3} + x} right)} right|_{ – 1}^1$ $ + left. {left( {frac{{{x^3}}}{3} – x} right)} right|_1^3$ $ = – frac{1}{3} + 1 + 9 – 3 – frac{1}{3} + 1$ $ – frac{1}{3} + 1 + 9 – 3 – frac{1}{3} + 1$ $ = frac{{44}}{3}.$
Vậy $I = int_{ – 3}^3 {left| {{x^2} – 1} right|} dx = frac{{44}}{3}.$Ví dụ 2: Tính tích phân: $I = int_0^2 {left| {{x^2} – 4x + 3} right|} dx.$Ta có bảng xét dấu: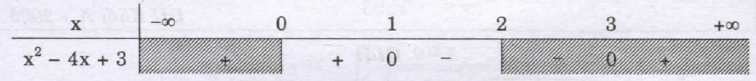 Nên $I = int_0^2 {left| {{x^2} – 4x + 3} right|} dx$ $ = int_0^1 {left( {{x^2} – 4x + 3} right)} dx$ $ + int_1^2 {left( { – {x^2} + 4x – 3} right)} dx$ $ = left. {left( {frac{{{x^3}}}{3} – 2{x^2} + 3x} right)} right|_0^1$ $ + left. {left( { – frac{{{x^3}}}{3} + 2{x^2} – 3x} right)} right|_1^2 = 2.$
Nên $I = int_0^2 {left| {{x^2} – 4x + 3} right|} dx$ $ = int_0^1 {left( {{x^2} – 4x + 3} right)} dx$ $ + int_1^2 {left( { – {x^2} + 4x – 3} right)} dx$ $ = left. {left( {frac{{{x^3}}}{3} – 2{x^2} + 3x} right)} right|_0^1$ $ + left. {left( { – frac{{{x^3}}}{3} + 2{x^2} – 3x} right)} right|_1^2 = 2.$
Vậy $I = int_0^2 {left| {{x^2} – 4x + 3} right|} dx = 2.$Ví dụ 3: Tính tích phân: ${I_{(m)}} = int_0^1 {left| {{x^2} – 2x + m} right|} dx.$Đặt $f(x) = {x^2} – 2x + m$ có $Delta’ = 1 – m.$
+ Khi $m ge 1$ $ Leftrightarrow Delta’ = 1 – m le 0$ $ Rightarrow f(x) ge 0$ $forall x in R.$
Do đó ${I_{(m)}} = int_0^1 {left| {{x^2} – 2x + m} right|} dx$ $ = int_0^1 {left( {{x^2} – 2x + m} right)} dx$ $ = left. {left( {frac{{{x^3}}}{3} – {x^2} + mx} right)} right|_0^1$ $ = m – frac{2}{3}.$
+ Khi $0 < m < 1$ thì $left{ {begin{array}{*{20}{l}}
{Delta’ = 1 – m > 0}\
{f(0) = m > 0}\
{f(1) = m – 1 < 0}
end{array}} right.$
Phương trình $f(x) = m$ có hai nghiệm ${x_1} < {x_2}.$
Do đó ta có $0 < {x_1} < 1 < {x_2}$ với ${x_1},{x_2} = 1 pm sqrt {1 – m} .$
Hay ta có: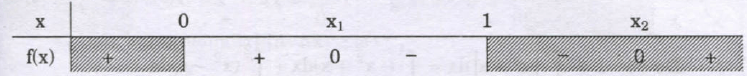 Nên: ${I_{(m)}} = int_0^1 {left| {{x^2} – 2x + m} right|} dx$ $ = int_0^{{x_1}} {left( {{x^2} – 2x + m} right)} dx$ $ + int_{{x_1}}^1 {left( { – {x^2} + 2x – m} right)} dx$ $ = left. {left( {frac{{{x^3}}}{3} – {x^2} + mx} right)} right|_0^{{x_1}}$ $ + left. {left( { – frac{{{x^3}}}{3} + {x^2} – mx} right)} right|_{{x_1}}^1$ $ = 2left[ {frac{{x_1^3}}{3} – x_1^2 + m{x_1}} right] + frac{2}{3} – m.$
Nên: ${I_{(m)}} = int_0^1 {left| {{x^2} – 2x + m} right|} dx$ $ = int_0^{{x_1}} {left( {{x^2} – 2x + m} right)} dx$ $ + int_{{x_1}}^1 {left( { – {x^2} + 2x – m} right)} dx$ $ = left. {left( {frac{{{x^3}}}{3} – {x^2} + mx} right)} right|_0^{{x_1}}$ $ + left. {left( { – frac{{{x^3}}}{3} + {x^2} – mx} right)} right|_{{x_1}}^1$ $ = 2left[ {frac{{x_1^3}}{3} – x_1^2 + m{x_1}} right] + frac{2}{3} – m.$
Thế ${x_1} = 1 – sqrt {1 – m} $ vào ta có:
${I_m} = frac{2}{3}(1 – sqrt {1 – m} )$$left[ {{{(1 – sqrt {1 – m} )}^2} – 3(1 – sqrt {1 – m} ) + 3m} right]$ $ + frac{2}{3} – m$ $ = frac{2}{3}(1 – sqrt {1 – m} )(2m – 1 + sqrt {1 – m} )$ $ + frac{2}{3} – m.$
+ Khi $m le 0$ thì $left{ {begin{array}{*{20}{l}}
{f(0) = m le 0}\
{f(1) = m – 1 le 0}
end{array}} right.$
Do đó ta có ${x_1} le 0 < 1 < {x_2}$ $ Rightarrow f(x) < 0$ $forall x in [0;1].$
Nên ${I_m} = int_0^1 {left( { – {x^2} + 2x – m} right)} dx$ $ = left. {left( {frac{{ – {x^3}}}{3} + {x^2} – mx} right)} right|_0^1$ $ = frac{2}{3} – m.$Ví dụ 4: Tính tích phân: $I = int_0^2 {left| {{x^2} – x} right|} dx.$Ta có: Do đó: $I = int_0^2 {left| {{x^2} – x} right|} dx$ $ = int_0^1 {left( { – {x^2} + x} right)} dx$ $ + int_1^2 {left( {{x^2} – x} right)} dx$ $ = left. {left( { – frac{{{x^3}}}{3} + frac{{{x^2}}}{2}} right)} right|_0^1$ $ + left. {left( {frac{{{x^3}}}{3} – frac{{{x^2}}}{2}} right)} right|_1^2 = 1.$Ví dụ 5: Tính tích phân: $I(alpha ) = int_0^1 x |x – alpha |dx.$+ Khi $alpha le 0$ thì $x – alpha ge 0$ $forall x in [0;1].$
Do đó: $I = int_0^2 {left| {{x^2} – x} right|} dx$ $ = int_0^1 {left( { – {x^2} + x} right)} dx$ $ + int_1^2 {left( {{x^2} – x} right)} dx$ $ = left. {left( { – frac{{{x^3}}}{3} + frac{{{x^2}}}{2}} right)} right|_0^1$ $ + left. {left( {frac{{{x^3}}}{3} – frac{{{x^2}}}{2}} right)} right|_1^2 = 1.$Ví dụ 5: Tính tích phân: $I(alpha ) = int_0^1 x |x – alpha |dx.$+ Khi $alpha le 0$ thì $x – alpha ge 0$ $forall x in [0;1].$
Vậy $I(alpha ) = int_0^1 x |x – alpha |dx$ $ = left. {left( {frac{{{x^3}}}{3} – frac{{alpha {x^2}}}{2}} right)} right|_0^1$ $ = frac{1}{3} – frac{alpha }{2}.$
+ Khi $0 < alpha < 1$, ta có: Vậy $I(alpha ) = int_0^alpha x |x – alpha |dx$ $ + int_alpha ^1 x |x – alpha |dx$ $ = int_0^alpha {left( { – {x^2} + alpha x} right)} dx$ $ + int_alpha ^1 {left( {{x^2} – alpha x} right)} dx$ $ = left. {left( {frac{{alpha {x^2}}}{2} – frac{{{x^3}}}{3}} right)} right|_0^alpha $ $ + left. {left( {frac{{{x^3}}}{3} – frac{{alpha {x^2}}}{2}} right)} right|_alpha ^1$ $ = frac{{{alpha ^3}}}{3} – frac{alpha }{2} + frac{1}{3}.$
Vậy $I(alpha ) = int_0^alpha x |x – alpha |dx$ $ + int_alpha ^1 x |x – alpha |dx$ $ = int_0^alpha {left( { – {x^2} + alpha x} right)} dx$ $ + int_alpha ^1 {left( {{x^2} – alpha x} right)} dx$ $ = left. {left( {frac{{alpha {x^2}}}{2} – frac{{{x^3}}}{3}} right)} right|_0^alpha $ $ + left. {left( {frac{{{x^3}}}{3} – frac{{alpha {x^2}}}{2}} right)} right|_alpha ^1$ $ = frac{{{alpha ^3}}}{3} – frac{alpha }{2} + frac{1}{3}.$
+ Khi $alpha ge 1$ thì $x – alpha le 0$ $forall x in [0;1].$
Vậy $I(alpha ) = int_0^1 {left( { – {x^2} + alpha x} right)} dx$ $ = left. {left( { – frac{{{x^3}}}{3} + frac{{alpha {x^2}}}{2}} right)} right|_0^1$ $ = frac{alpha }{2} – frac{1}{3}.$Ví dụ 6: Cho $f(x) = 3{x^3} – {x^2} – 4x + 1$ và $g(x) = 2{x^3} + {x^2} – 3x – 1.$
a) Giải bất phương trình $f(x) ge g(x).$
b) Tính $I = int_{ – 1}^2 | f(x) – g(x)|dx.$a) Ta có: $f(x) ge g(x)$ $ Leftrightarrow f(x) – g(x) ge 0$ $ Leftrightarrow {x^3} – 2x – x + 2 ge 0$ $ Leftrightarrow (x – 1)left( {{x^2} – x – 2} right) ge 0$ $ Leftrightarrow left( {{x^2} – 1} right)(x – 2) ge 0$ $ Leftrightarrow – 1 le x le 1$ hoặc $x ge 2.$
b) Ta có: (dựa vào câu a, ta xác định được $f(x) – g(x)$ âm, dương khi nào). Vậy $I = int_{ – 1}^2 | f(x) – g(x)|dx$ $ = int_{ – 1}^1 | f(x) – g(x)|dx$ $ + int_1^2 | f(x) – g(x)|dx$ $ = intlimits_{ – 1}^1 {left[ {fleft( x right) – gleft( x right)} right]dx} $ $ – intlimits_1^2 {left[ {fleft( x right) – gleft( x right)} right]dx} $ $ = int_{ – 1}^1 {left( {{x^3} – 2{x^2} – x + 2} right)} dx$ $ – int_1^2 {left( {{x^3} – 2{x^2} – x + 2} right)} dx$ $ = left. {left( {frac{{{x^4}}}{4} – frac{{2{x^2}}}{3} – frac{{{x^2}}}{2} + 2x} right)} right|_{ – 1}^1$ $ – left. {left( {frac{{{x^4}}}{4} – frac{{2{x^2}}}{3} – frac{{{x^2}}}{2} + 2x} right)} right|_1^2 = frac{{37}}{{12}}.$Ví dụ 7: Tính tích phân: $I = int_{ – pi }^pi {sqrt {1 – sin x} } dx.$Ta có: $I = int_{ – pi }^pi {sqrt {{{left( {sin frac{x}{2} – cos frac{x}{2}} right)}^2}} } dx$ $ = int_{ – pi }^pi {left| {sin frac{x}{2} – cos frac{x}{2}} right|} dx$ $ = sqrt 2 int_{ – pi }^pi {left| {cos left( {frac{x}{2} + frac{pi }{4}} right)} right|} dx.$
Vậy $I = int_{ – 1}^2 | f(x) – g(x)|dx$ $ = int_{ – 1}^1 | f(x) – g(x)|dx$ $ + int_1^2 | f(x) – g(x)|dx$ $ = intlimits_{ – 1}^1 {left[ {fleft( x right) – gleft( x right)} right]dx} $ $ – intlimits_1^2 {left[ {fleft( x right) – gleft( x right)} right]dx} $ $ = int_{ – 1}^1 {left( {{x^3} – 2{x^2} – x + 2} right)} dx$ $ – int_1^2 {left( {{x^3} – 2{x^2} – x + 2} right)} dx$ $ = left. {left( {frac{{{x^4}}}{4} – frac{{2{x^2}}}{3} – frac{{{x^2}}}{2} + 2x} right)} right|_{ – 1}^1$ $ – left. {left( {frac{{{x^4}}}{4} – frac{{2{x^2}}}{3} – frac{{{x^2}}}{2} + 2x} right)} right|_1^2 = frac{{37}}{{12}}.$Ví dụ 7: Tính tích phân: $I = int_{ – pi }^pi {sqrt {1 – sin x} } dx.$Ta có: $I = int_{ – pi }^pi {sqrt {{{left( {sin frac{x}{2} – cos frac{x}{2}} right)}^2}} } dx$ $ = int_{ – pi }^pi {left| {sin frac{x}{2} – cos frac{x}{2}} right|} dx$ $ = sqrt 2 int_{ – pi }^pi {left| {cos left( {frac{x}{2} + frac{pi }{4}} right)} right|} dx.$
Đổi biến: đặt $t = frac{x}{2} + frac{pi }{4} Rightarrow dt = frac{{dx}}{2}.$
Đổi cận: $left[ {begin{array}{*{20}{l}}
{x = pi }\
{x = – pi }
end{array}} right.$ $ Rightarrow left[ {begin{array}{*{20}{l}}
{t = frac{{3pi }}{4}}\
{t = – frac{pi }{4}}
end{array}} right.$
Ta thấy: với $ – frac{pi }{4} le t le frac{pi }{2}$ thì $cos t ge 0$, với $frac{pi }{2} le t le frac{{3pi }}{4}$ thì $cos t < 0.$
Suy ra: $I = 2sqrt 2 int_{ – frac{pi }{4}}^{frac{{3pi }}{4}} | cos t|dt$ $ = 2sqrt 2 int_{ – frac{pi }{4}}^{frac{pi }{2}} {cos } tdt – 2sqrt 2 int_{frac{pi }{2}}^{frac{{3pi }}{4}} { cos tdt } $ $ = 2sqrt 2 sin left. t right|_{ – frac{pi }{4}}^{frac{pi }{2}} – 2sqrt 2 sin left. t right|_{frac{pi }{2}}^{frac{{3pi }}{4}} = 4sqrt 2 .$Ví dụ 8: Tính tích phân: $I = int_{ – frac{pi }{2}}^{frac{pi }{2}} | sin x|dx.$Ta có: $I = int_{ – frac{pi }{2}}^{frac{pi }{2}} | sin x|dx$ $ = int_{ – frac{pi }{2}}^0 {( – sin x)} dx + int_0^{frac{pi }{2}} {sin } xdx$ $ = cos left. x right|_{ – frac{pi }{2}}^0 + left. {( – cos x)} right|_0^{frac{pi }{2}}$ $ = 1 + 1 = 2.$Ví dụ 9: Tính $I = int_{frac{pi }{4}}^{frac{{3pi }}{4}} | sin 2x|dx.$Đặt $t = 2x Rightarrow dt = 2dx.$
Đổi cận $left[ {begin{array}{*{20}{l}}
{x = frac{{3pi }}{4}}\
{x = frac{pi }{4}}
end{array}} right.$ $ Rightarrow left[ {begin{array}{*{20}{l}}
{t = frac{{3pi }}{2}}\
{t = frac{pi }{2}}
end{array}} right.$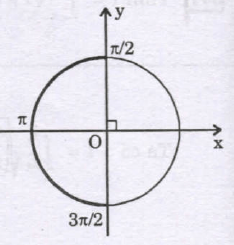 Do đó: $I = frac{1}{2}int_{frac{pi }{2}}^{frac{{3pi }}{2}} | sin t|dt$ $ = frac{1}{2}int_{frac{pi }{2}}^pi | sin t|dt + frac{1}{2}int_pi ^{frac{{3pi }}{2}} | sin t|dt$ $ = frac{1}{2}int_{frac{pi }{2}}^pi {sin t} dt – frac{1}{2}int_pi ^{frac{{3pi }}{2}} {sin } tdt$ (vì $frac{pi }{2} le t le pi $ thì $sin t ge 0$, $frac{pi }{2} le t le frac{{3pi }}{2}$ thì $sin t le 0$).
Do đó: $I = frac{1}{2}int_{frac{pi }{2}}^{frac{{3pi }}{2}} | sin t|dt$ $ = frac{1}{2}int_{frac{pi }{2}}^pi | sin t|dt + frac{1}{2}int_pi ^{frac{{3pi }}{2}} | sin t|dt$ $ = frac{1}{2}int_{frac{pi }{2}}^pi {sin t} dt – frac{1}{2}int_pi ^{frac{{3pi }}{2}} {sin } tdt$ (vì $frac{pi }{2} le t le pi $ thì $sin t ge 0$, $frac{pi }{2} le t le frac{{3pi }}{2}$ thì $sin t le 0$).
$I = – frac{1}{2}cos left. t right|_{frac{pi }{2}}^pi + frac{1}{2}cos left. t right|_pi ^{frac{{3pi }}{2}} = 1.$Ví dụ 10: Tính tích phân: $I = int_{frac{pi }{6}}^{frac{pi }{3}} {sqrt {{{tan }^2}x + {{cot }^2}x – 2} } dx.$Ta có: $sqrt {{{tan }^2}x + {{cot }^2}x – 2} $ $ = sqrt {{{(tan x + cot x)}^2}} $ $ = |tan x – cot x|$ $ = left| {frac{{sin x}}{{cos x}} – frac{{cos x}}{{sin x}}} right|$ $ = left| {frac{{{{sin }^2}x – {{cos }^2}x}}{{sin xcos x}}} right|$ $ = left| {frac{{{{cos }^2}x – {{sin }^2}x}}{{sin xcos x}}} right|$ $ = 2left| {frac{{cos 2x}}{{sin 2x}}} right|.$
Ta có: $frac{pi }{6} le x le frac{pi }{3}$ $ Rightarrow frac{pi }{3} le 2x le frac{{2pi }}{3}.$
Do đó: $sin 2x ge 0$, $left{ begin{array}{l}
cos 2x le 0:{rm{khi}}:x in left[ {frac{pi }{4};frac{pi }{3}} right]\
cos 2x ge 0:{rm{khi}}:x in left[ {frac{pi }{6};frac{pi }{4}} right]
end{array} right.$
Vậy $I = int_{frac{pi }{6}}^{frac{pi }{4}} 2 left| {frac{{cos 2x}}{{sin 2x}}} right|dx$ $ + int_{frac{pi }{4}}^{frac{pi }{3}} 2 left| {frac{{cos 2x}}{{sin 2x}}} right|dx$ $ = int_{frac{pi }{6}}^{frac{pi }{4}} 2 frac{{cos 2x}}{{sin 2x}}dx – int_{frac{pi }{4}}^{frac{pi }{3}} 2 frac{{cos 2x}}{{sin 2x}}dx$ $ = int_{frac{pi }{6}}^{frac{pi }{4}} 2 frac{{d(sin 2x)}}{{sin 2x}} – int_{frac{pi }{4}}^{frac{pi }{3}} 2 frac{{d(sin 2x)}}{{sin 2x}}$ $ = ln left. {|sin 2x|} right|_{frac{pi }{6}}^{frac{pi }{4}} – left. {ln |sin 2x|} right|_{frac{pi }{4}}^{frac{pi }{3}}$ $ = left( {ln 1 – ln frac{{sqrt 3 }}{2}} right) – left( {ln frac{{sqrt 3 }}{2} – ln 1} right)$ $ = – 2ln frac{{sqrt 3 }}{2}.$Ví dụ 11: Tính tích phân: $I = int_0^pi {sqrt {1 + cos 2x} } dx.$Ta có: $I = int_0^pi {sqrt {1 + cos 2x} } dx$ $ = int_0^pi {sqrt {2{{cos }^2}x} } dx$ $ = int_0^pi {sqrt 2 } |cos x|dx$ $ = sqrt 2 int_0^{frac{pi }{2}} {cos } xdx – sqrt 2 int_{frac{pi }{2}}^pi {cos } xdx$ $ = sqrt 2 sin left. x right|_0^{frac{pi }{2}} – sqrt 2 sin left. x right|_{frac{pi }{2}}^pi $ $ = 2sqrt 2 .$Ví dụ 12: Tính tích phân: $I = int_0^pi | cos x|sqrt {sin x} dx.$Ta có: $I = int_0^pi | cos x|sqrt {sin x} dx$ $ + int_{frac{pi }{2}}^pi | cos x|sqrt {sin x} dx$ $ = int_0^{frac{pi }{2}} {cos } x.{(sin x)^{frac{1}{2}}}dx$ $ – int_{frac{pi }{2}}^pi {cos } x.{(sin x)^{frac{1}{2}}}dx$ $ = int_0^{frac{pi }{2}} {{{(sin x)}^{frac{1}{2}}}} d(sin x)$ $ – int_{frac{pi }{2}}^pi {{{(sin x)}^{frac{1}{2}}}} d(sin x)$ $ = frac{2}{3}left. {{{(sin x)}^{frac{3}{2}}}} right|_0^{frac{pi }{2}} – frac{2}{3}left. {{{(sin x)}^{frac{3}{2}}}} right|_{frac{pi }{2}}^pi $ $ = frac{2}{3} + frac{2}{3} = frac{4}{3}.$Ví dụ 13: Tính tích phân: $I = int_{ – 1}^1 {frac{{|x|dx}}{{{x^4} – {x^2} – 12}}} .$Vì hàm số $f(x) = frac{{|x|}}{{{x^4} – {x^2} – 12}}$ là hàm số chẵn, liên tục trong $[ – 1;1].$
Suy ra: $I = int_{ – 1}^1 {frac{{|x|dx}}{{{x^4} – {x^2} – 12}}} $ $ = 2int_0^1 {frac{{|x|dx}}{{{x^4} – {x^2} – 12}}} $ $ = 2int_0^1 {frac{{xdx}}{{{x^4} – {x^2} – 12}}} .$
Đặt $t = {x^2} Rightarrow dt = 2xdx.$
Đổi cận $left[ {begin{array}{*{20}{l}}
{x = 1}\
{x = 0}
end{array}} right.$ $ Rightarrow left[ {begin{array}{*{20}{l}}
{t = 1}\
{t = 0}
end{array}} right.$
Vậy $I = int_0^1 {frac{{dt}}{{{t^2} – t – 12}}} $ $ = int_0^1 {frac{{dt}}{{(t – 4)(t + 3)}}} $ $ = frac{1}{7}int_0^1 {left( {frac{1}{{t – 4}} – frac{1}{{t + 3}}} right)} dt$ $ = frac{1}{7}ln left. {left| {frac{{t – 4}}{{t + 3}}} right|} right|_0^1$ $ = frac{2}{7}ln frac{3}{4}.$

Be the first to comment