
Bài viết hướng dẫn phương pháp ứng dụng tích phân để tính thể tích khối tròn xoay khi quay quanh Ox hình phẳng giới hạn bởi một đường cong và trục hoành.I. KIẾN THỨC CẦN NHỚ
1. Cho hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$ liên tục trên đoạn $[a;b]$, trục $Ox$ và hai đường thẳng $x= a$, $x=b$ quay quanh $Ox$ ta được khối tròn xoay có thể tích là: $V = pi int_a^b {{f^2}} (x)dx.$ 2. Cho hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$ và trục hoành quay quanh $Ox$ ta được khối tròn xoay có thể tích là $V = pi int_alpha ^beta {{f^2}} (x)dx$, trong đó $alpha $, $beta $ lần lượt là nghiệm nhỏ nhất và lớn nhất của phương trình $f(x) = 0.$II. BÀI TẬP TRẮC NGHIỆM MINH HỌA
2. Cho hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$ và trục hoành quay quanh $Ox$ ta được khối tròn xoay có thể tích là $V = pi int_alpha ^beta {{f^2}} (x)dx$, trong đó $alpha $, $beta $ lần lượt là nghiệm nhỏ nhất và lớn nhất của phương trình $f(x) = 0.$II. BÀI TẬP TRẮC NGHIỆM MINH HỌA
Ví dụ 1: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$ liên tục trên đoạn $[a;b]$, trục $Ox$ và hai đường thẳng $x= a$, $x = b$ quay quanh $Ox$ được tính bởi công thức nào sau đây?
A. $V = int_a^b {{f^2}} (x)dx.$
B. $V = pi int_a^b f (x)dx.$
C. $V = int_a^b | f(x)|dx.$
D. $V = pi int_a^b {{f^2}} (x)dx.$Lời giải:
Theo lý thuyết ta có $V = pi int_a^b {{f^2}} (x)dx.$
Chọn đáp án D.Ví dụ 2: Cho hàm số $y=f(x)$ liên tục trên đoạn $[a;b].$ Hình phẳng giới hạn bởi các đường $y = f(x)$, $y=0$, $x= a$, $x=b$ quay quanh trục $Ox$ có thể tích là ${V_1}.$ Hình phẳng giới hạn bởi các đường $y = sqrt {2018} f(x)$, $y=0$, $x= a$, $x=b$ quay quanh trục $Ox$ có thể tích là ${V_2}.$ Khẳng định nào sau đây là đúng?
A. ${V_1} = 2018{V_2}.$
B. ${V_2} = 2018{V_1}.$
C. ${V_1} = sqrt {2018} {V_2}.$
D. ${V_2} = sqrt {2018} {V_1}.$Lời giải:
${V_1} = pi int_a^b {{f^2}} (x)dx.$
${V_2} = pi int_a^b {{{[sqrt {2018} f(x)]}^2}dx} $ $ = 2018pi int_a^b {{f^2}} (x)dx.$
${V_2} = 2018{V_1}.$
Chọn đáp án B.Ví dụ 3: Cho hình phẳng $H$ giới hạn bởi đường cong $y = sqrt {3{x^2} + 2} $, trục hoành và các đường thẳng $x=0$, $x=2.$ Khối tròn xoay tạo thành khi quay $H$ quanh trục hoành có thể tích bằng:
A. $8pi .$
B. $10pi .$
C. $12pi .$
D. $14pi .$Lời giải:
$V = pi int_0^2 {left( {3{x^2} + 2} right)dx} $ $ = left. {pi left( {{x^3} + 2x} right)} right|_0^2$ $ = 12pi .$
Chọn đáp án C.Ví dụ 4: Cho hình phẳng $H$ giới hạn bởi các đường $y=2x+1$, $y=0$, $x=0$, $x=1.$ Khối tròn xoay tạo thành khi quay $H$ quanh trục hoành có thể tích bằng:
A. ${2pi .}$
B. ${3pi .}$
C. ${frac{9}{2}.}$
D. ${frac{{13pi }}{3}}.$Lời giải:
$V = pi int_0^1 {{{(2x + 1)}^2}} dx$ $ = left. {pi frac{{{{(2x + 1)}^3}}}{6}} right|_0^1$ $ = frac{{13pi }}{3}.$
Chọn đáp án D.Ví dụ 5: Cho hình phẳng $H$ giới hạn bởi các đường $y = x – {x^2}$ và trục hoành. Khối tròn xoay tạo thành khi quay $H$ quanh trục hoành có thể tích bằng:
A. $frac{1}{{30}}.$
B. $frac{pi }{{30}}.$
C. $frac{1}{6}.$
D. $frac{pi }{6}.$Lời giải:
Tìm hoành độ giao điểm: $x – {x^2} = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 0}\
{x = 1}
end{array}} right..$
Thể tích: $V = pi int_0^1 {{{left( {x – {x^2}} right)}^2}} dx = frac{pi }{{30}}.$
Chọn đáp án B.Ví dụ 6: Cho hình phẳng $H$ giới hạn bởi các đường $y = sqrt {1 – {x^2}} $ và trục hoành. Khối tròn xoay tạo thành khi quay $H$ quanh trục hoành có thể tích bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $T = 2a +b.$
A. $T=-11.$
B. $T=-10.$
C. $T =10.$
D. $T=11.$Lời giải:
Tìm hoành độ giao điểm: $sqrt {1 – {x^2}} = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = – 1}\
{x = 1}
end{array}} right..$
Thể tích: $V = pi int_{ – 1}^1 {left( {1 – {x^2}} right)dx} = frac{{4pi }}{3}$ $ Rightarrow a = 4$, $b = 3$ $ Rightarrow T = 2a + b = 11.$
Chọn đáp án D.Ví dụ 7: Cho hình phẳng $H$ giới hạn bởi các đường $y = sqrt {sin x} $, $y = 0$, $x = 0$, $x = frac{{3pi }}{4}.$ Khối tròn xoay tạo thành khi quay $H$ quanh trục hoành có thể tích $V$ bằng bao nhiêu?
A. $V = frac{{pi sqrt 2 }}{2}.$
B. $V = pi left( {frac{{sqrt 2 }}{2} – 1} right).$
C. $V = pi left( {frac{{sqrt 2 }}{2} + 1} right).$
D. $V = frac{{sqrt 2 }}{2} + 1.$Lời giải:
$V = pi int_0^{frac{{3pi }}{4}} {sin xdx} $ $ = – left. {pi cos x} right|_0^{frac{{3pi }}{4}}$ $ = pi left( {frac{{sqrt 2 }}{2} + 1} right).$
Chọn đáp án C.Ví dụ 8: Cho hình phẳng $H$ giới hạn bởi các đường $y = cos x$, $y = 0$, $x = 0$, $x = frac{pi }{2}.$ Khối tròn xoay tạo thành khi quay $H$ quanh trục hoành có thể tích $V$ bằng bao nhiêu?
A. $V = frac{pi }{4}.$
B. $V = frac{{{pi ^2}}}{4}.$
C. $V = frac{pi }{2}left( {frac{pi }{2} – 1} right).$
D. $V = frac{pi }{2}left( {frac{pi }{2} + 1} right).$ Lời giải:
$V = pi int_0^{frac{pi }{2}} {{{cos }^2}} xdx$ $ = frac{pi }{2}int_0^{frac{pi }{2}} {(1 + cos 2x)dx} $ $ = left. {frac{pi }{2}left( {x + frac{1}{2}sin 2x} right)} right|_0^{frac{pi }{2}}$ $ = frac{{{pi ^2}}}{4}.$
Chọn đáp án B.Ví dụ 9: Cho hình phẳng $H$ giới hạn bởi các đường $y = sin x$, $y = 0$, $x = 0$, $x = frac{pi }{4}.$ Khối tròn xoay tạo thành khi quay $H$ quanh trục hoành có thể tích $V$ bằng bao nhiêu?
A. $V = frac{1}{2}left( {frac{pi }{4} + frac{{sqrt 2 }}{2}} right).$
B. $V = frac{1}{2}left( {frac{pi }{4} – frac{{sqrt 2 }}{2}} right).$
C. $V = frac{pi }{2}left( {frac{pi }{4} – frac{1}{2}} right).$
D. $V = frac{pi }{2}left( {frac{pi }{4} + frac{1}{2}} right).$Lời giải:
$V = pi int_0^{frac{pi }{4}} {{{sin }^2}} xdx$ $ = frac{pi }{2}int_0^{frac{pi }{4}} {(1 – cos 2x)dx} $ $ = left. {frac{pi }{2}left( {x – frac{1}{2}sin 2x} right)} right|_0^{frac{pi }{4}}$ $ = frac{pi }{2}left( {frac{pi }{4} – frac{1}{2}} right).$
Chọn đáp án C.Ví dụ 10: Cho hình phẳng $H$ giới hạn bởi các đường $y = tan x$, $y = 0$, $x = 0$, $x = frac{pi }{4}.$ Khối tròn xoay tạo thành khi quay $H$ quanh trục hoành có thể tích $V$ bằng bao nhiêu?
A. $V = 1 – frac{pi }{4}.$
B. $V = pi left( {1 – frac{pi }{4}} right).$
C. $V = frac{pi }{3}.$
D. $V = 2pi .$Lời giải:
$V = pi int_0^{frac{pi }{4}} {{{tan }^2}} xdx$ $ = pi int_0^{frac{pi }{4}} {left( {frac{1}{{{{cos }^2}x}} – 1} right)dx} $ $ = left. {pi (tan x – x)} right|_0^{frac{pi }{4}}$ $ = pi left( {1 – frac{pi }{4}} right).$
Chọn đáp án B.Ví dụ 11: Cho hình phẳng $H$ giới hạn bởi các đường $y = sin x + cos x$, $y = 0$, $x = 0$, $x = frac{pi }{2}.$ Khối tròn xoay tạo thành khi quay $H$ quanh trục hoành có thể tích $V$ bằng bao nhiêu?
A. $V = pi left( {frac{1}{2} + frac{pi }{4}} right).$
B. $V = pi left( {1 + frac{pi }{4}} right).$
C. $V = pi left( {frac{pi }{2} + 1} right).$
D. $V = frac{{pi (pi + 1)}}{2}.$Lời giải:
$V = pi int_0^{frac{pi }{2}} {{{(sin x + cos x)}^2}} dx$ $ = pi int_0^{frac{pi }{2}} {(1 + sin 2x)dx} $ $ = left. {pi left( {x – frac{1}{2}cos 2x} right)} right|_0^{frac{pi }{2}}$ $ = pi left( {frac{pi }{2} + 1} right).$
Chọn đáp án C.Ví dụ 12: Cho hình phẳng $H$ giới hạn bởi các đường $y = sqrt {2 + sin x – cos x} $, $y = 0$, $x = 0$, $x = frac{pi }{2}.$ Khối tròn xoay tạo thành khi quay $H$ quanh trục hoành có thể tích $V$ bằng bao nhiêu?
A. $V = frac{pi }{2}.$
B. $V = pi .$
C. $V = frac{{{pi ^2}}}{2}.$
D. $V = {pi ^2}.$Lời giải:
$V = pi int_0^{frac{pi }{2}} {(2 + sin x – cos x)dx} $ $ = left. {pi (2x – cos x – sin x)} right|_0^{frac{pi }{2}}$ $ = {pi ^2}.$
Chọn đáp án D.Ví dụ 13: Cho hình phẳng $H$ giới hạn bởi các đường $y = sqrt {1 + cos x} $, $y = 0$, $x = 0$, $x = frac{pi }{6}.$ Khối tròn xoay tạo thành khi quay $H$ quanh trục hoành có thể tích bằng $frac{{{pi ^2}}}{a} + frac{pi }{b}$ với $a$, $b$ là các số nguyên. Khẳng định nào sau đây là đúng?
A. $a+2b = 10.$
B. $a<b.$
C. $a>2b.$
D. $2a+b=10.$Lời giải:
$V = pi int_0^{frac{pi }{6}} {(1 + cos x)dx} $ $ = left. {pi (x + sin x)} right|_0^{frac{pi }{6}}$ $ = pi left( {frac{pi }{6} + frac{1}{2}} right)$ $ = frac{{{pi ^2}}}{6} + frac{pi }{2}$ $ Rightarrow a = 6$, $b = 2.$
$ Rightarrow a + 2b = 10.$
Chọn đáp án A.Ví dụ 14: Cho hình phẳng $D$ giới hạn bởi đường cong $y = sqrt {2 + sin x} $, trục hoành và các đường thẳng $x = 0$, $x = pi .$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích $V$ bằng bao nhiêu?
A. $V = 2{pi ^2}.$
B. $V = 2pi (pi + 1).$
C. $V = 2pi .$
D. $V = 2(pi + 1).$Lời giải:
$V = pi int_0^pi {{{(sqrt {2 + sin x} )}^2}} dx$ $ = pi int_0^pi {(2 + sin x)dx} $ $ = left. {pi (2x – cos x)} right|_0^pi $ $ = 2pi (pi + 1).$
Chọn đáp án B.Ví dụ 15: Cho hình phẳng $D$ giới hạn bởi đường cong $y = 1 + 2sin x$, trục hoành và các đường thẳng $x = 0$, $x = frac{pi }{2}.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng $frac{a}{b}{pi ^2} + cpi $ với $a$, $b$, $c$ là các số nguyên dương, $frac{a}{b}$ là phân số tối giản. Tính $T = a + {b^2} + c.$
A. $T=11.$
B. $T=15.$
C. $T = 21.$
D. $T=25.$Lời giải:
$V = pi int_0^{frac{pi }{2}} {{{(1 + 2sin x)}^2}} dx$ $ = pi int_0^{frac{pi }{2}} {left( {1 + 4sin x + 4{{sin }^2}x} right)dx} .$
$ = pi int_0^{frac{pi }{2}} {(3 + 4sin x – 2cos 2x)dx} $ $ = left. {pi (3x – 4cos x – sin 2x)} right|_0^{frac{pi }{2}}$ $ = frac{{3{pi ^2}}}{2} + 4pi .$
$ Rightarrow a = 3$, $b = 2$, $c = 4$ $ Rightarrow T = a + {b^2} + c = 11.$
Chọn đáp án A.Ví dụ 16: Cho hình phẳng $D$ giới hạn bởi đường cong $y = sqrt {{{sin }^4}x + {{cos }^4}x} $, trục hoành và các đường thẳng $x = 0$, $x = frac{pi }{2}.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng $frac{a}{b}{pi ^2}$ với $a$, $b$ là các số nguyên dương, $frac{a}{b}$ là phân số tối giản. Tính $T= 2a + 3b.$
A. $T = 25.$
B. $T= 30.$
C. $T = 35.$
D. $T = 40.$Lời giải:
$V = pi int_0^{frac{pi }{2}} {left( {{{sin }^4}x + {{cos }^4}x} right)dx} $ $ = pi int_0^{frac{pi }{2}} {left( {frac{3}{4} + frac{1}{4}cos 2x} right)dx} .$
$ = left. {pi left( {frac{{3x}}{4} + frac{1}{8}sin 2x} right)} right|_0^{frac{pi }{2}}$ $ = frac{{3{pi ^2}}}{8}.$
$ Rightarrow a = 3$, $b = 8$ $ Rightarrow T = 2a + 3b = 30.$
Chọn đáp án B.Ví dụ 17: Cho hình phẳng $D$ giới hạn bởi đường cong $y = sqrt {xcos x} $, trục hoành và các đường thẳng $x = 0$, $x = frac{pi }{2}.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng $frac{{{pi ^2}}}{a} + bpi $ với $a$, $b$ là các số nguyên. Tính $T = a – b + ab.$
A. $T=1.$
B. $T = 2.$
C. $T=3.$
D. $T=4.$Lời giải:
$V = pi int_0^{frac{pi }{2}} x cos xdx.$ $V = left. {pi (xsin x + cos x)} right|_0^{frac{pi }{2}}$ $ = frac{{{pi ^2}}}{2} – pi $ $ Rightarrow a = 2$, $b = – 1$ $ Rightarrow T = a – b + ab = 1.$
$V = left. {pi (xsin x + cos x)} right|_0^{frac{pi }{2}}$ $ = frac{{{pi ^2}}}{2} – pi $ $ Rightarrow a = 2$, $b = – 1$ $ Rightarrow T = a – b + ab = 1.$
Chọn đáp án A.Ví dụ 18: Cho hình phẳng $D$ giới hạn bởi đường cong $y = sqrt {x(2 – sin x)} $, trục hoành và các đường thẳng $x = frac{pi }{2}.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng $pi left( {frac{{{pi ^2}}}{a} – b} right)$ với $a$, $b$ là các số nguyên. Tính $T = {a^2} + {b^2} – a.$
A. $T = 13.$
B. $T=16.$
D. $T = 21.$
C. $T = 18.$Lời giải:
Tìm hoành độ giao điểm: $sqrt {x(2 – sin x)} = 0$ $ Leftrightarrow x = 0.$
Thể tích: $V = pi int_0^{frac{pi }{2}} x (2 – sin x)dx.$ $V = left. {pi left[ {x(2x + cos x) – left( {{x^2} + sin x} right)} right]} right|_0^{frac{pi }{2}}$ $ = pi left( {frac{{{pi ^2}}}{4} – 1} right)$ $ Rightarrow a = 4$, $b = 1.$
$V = left. {pi left[ {x(2x + cos x) – left( {{x^2} + sin x} right)} right]} right|_0^{frac{pi }{2}}$ $ = pi left( {frac{{{pi ^2}}}{4} – 1} right)$ $ Rightarrow a = 4$, $b = 1.$
$ Rightarrow T = {a^2} + {b^2} – a = 13.$
Chọn đáp án A.Ví dụ 19: Cho hình phẳng $D$ giới hạn bởi đường cong $y = {e^x}$, trục hoành và các đường thẳng $x=0$, $x=1.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích $V$ bằng bao nhiêu?
A. $V = frac{{pi {e^2}}}{2}.$
B. $V = frac{{pi left( {{e^2} + 1} right)}}{2}.$
C. $V = frac{{{e^2} – 1}}{2}.$
D. $V = frac{{pi left( {{e^2} – 1} right)}}{2}.$Lời giải:
$V = pi int_0^1 {{e^{2x}}} dx$ $ = left. {frac{pi }{2}{e^{2x}}} right|_0^1 = frac{{pi left( {{e^2} – 1} right)}}{2}.$
Chọn đáp án D.Ví dụ 20: Cho hình phẳng $D$ giới hạn bởi đường cong $y = 2 + {e^x}$, trục hoành và các đường thẳng $x=0$, $x=1.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng $pi left( {frac{{{e^2}}}{a} + be + frac{1}{c}} right)$ với $a$, $b$, $c$ là các số nguyên. Tính $T=a+2b+3c.$
A. $T=4.$
B. $T=6.$
C. $T=14.$
D. $T =16.$Lời giải:
$V = pi int_0^1 {{{left( {2 + {e^x}} right)}^2}} dx$ $ = pi int_0^1 {left( {4 + 4{e^x} + {e^{2x}}} right)dx} .$
$ = left. {pi left( {4x + 4{e^x} + frac{1}{2}{e^{2x}}} right)} right|_0^1$ $ = pi left( {frac{{{e^2}}}{2} + 4e – frac{1}{2}} right).$
$ Rightarrow a = 2$, $b = 4$, $c = – 2$ $ Rightarrow T = a + 2b + 3c = 4.$
Chọn đáp án A.Ví dụ 21: Cho hình phẳng $D$ giới hạn bởi đường cong $y = sqrt {4x + {e^x}} $, trục hoành và các đường thẳng $x=0$, $x=1.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng $pi (a + be)$ với $a$, $b$ là các số nguyên. Tính $T = a + 5b + {log _{2018}}a.$
A. $T=4.$
B. $T=6.$
C. $T=7.$
D. $T=9.$Lời giải:
$V = pi int_0^1 {left( {4x + {e^x}} right)dx} $ $ = left. {pi left( {2{x^2} + {e^x}} right)} right|_0^1$ $ = pi (1 + e)$ $ Rightarrow a = 1$, $b = 1.$
$ Rightarrow T = a + 5b + {log _{2018}}a = 6.$
$ Rightarrow T = a + 5b + {log _{2018}}a = 6.$
Chọn đáp án B.Ví dụ 22: Cho hình phẳng $D$ giới hạn bởi đường cong $y = {e^x} + {e^{ – x}}$, trục hoành và các đường thẳng $x=0$, $x=1.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng $pi left( {frac{{{e^2}}}{a} + frac{{{e^{ – 2}}}}{b} + c} right)$ với $a$, $b$, $c$ là các số nguyên.
Tính $T=a+b+2c.$
A. $T=-2.$
B. $T=0.$
C. $T=2.$
D. $T = 4.$Lời giải:
$V = pi int_0^1 {{{left( {{e^x} + {e^{ – x}}} right)}^2}} dx$ $ = pi int_0^1 {left( {{e^{2x}} + 2 + {e^{ – 2x}}} right)dx} .$
$ = left. {pi left( {frac{{{e^{2x}}}}{2} + 2x – frac{{{e^{ – 2x}}}}{2}} right)} right|_0^1$ $ = pi left( {frac{{{e^2}}}{2} + 2 – frac{{{e^{ – 2}}}}{2}} right).$
$ Rightarrow a = 2$, $b = – 2$, $c = 2$ $ Rightarrow T = a + b + 2c = 4.$
Chọn đáp án D.Ví dụ 23: Cho hình phẳng $D$ giới hạn bởi đường cong $y = sqrt {{e^{2x}} – {e^x}} $, trục hoành và đường thẳng $x=1.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng $pi left( {frac{{{e^2}}}{a} – e + frac{1}{b}} right)$ với $a$, $b$ là các số nguyên. Điểm $M(a;b)$ thuộc đồ thị hàm số nào sau đây?
A. $y = 5x + 1.$
B. $y = {x^2}.$
C. $y = {x^3} – 6.$
D. $y = {x^4} – 2.$Lời giải:
Hoành độ giao điểm:
$sqrt {{e^{2x}} – {e^x}} = 0$ $ Leftrightarrow x = 0.$
Thể tích: $V = pi int_0^1 {left( {{e^{2x}} – {e^x}} right)dx} $ $ = left. {pi left( {frac{1}{2}{e^{2x}} – {e^x}} right)} right|_0^1$ $ = pi left( {frac{{{e^2}}}{2} – e + frac{1}{2}} right).$
$ Rightarrow a = 2$, $b = 2$ $ Rightarrow M(2;2)$ thuộc đồ thị hàm số $y = {x^3} – 6.$
Chọn đáp án C.Ví dụ 24: Cho hình phẳng $D$ giới hạn bởi đường cong $y = sqrt {(1 – x){e^x}} $, trục hoành và trục tung. Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng $pi (ae + b)$ với $a$, $b$ là các số nguyên. Điểm $I(a;b)$ là đỉnh của parabol nào sau đây?
A. $y = {x^2} – 3.$
B. $y = {x^2} – 2x + 1.$
C. $y = {x^2} + 2x – 5.$
D. $y = {x^2} – 2x – 1.$Lời giải:
Hoành độ giao điểm: $sqrt {(1 – x){e^x}} = 0$ $ Leftrightarrow x = 1.$
Thể tích: $V = pi int_0^1 {(1 – x){e^x}dx} .$ $V = left. {pi left[ {(1 – x){e^x} + {e^x}} right]} right|_0^1$ $ = pi (e – 2)$ $ Rightarrow a = 1$, $b = – 2.$
$V = left. {pi left[ {(1 – x){e^x} + {e^x}} right]} right|_0^1$ $ = pi (e – 2)$ $ Rightarrow a = 1$, $b = – 2.$
$ Rightarrow I(1; – 2)$ là đỉnh của parabol $y = {x^2} – 2x – 1.$
Chọn đáp án D.Ví dụ 25: Cho hình phẳng $D$ giới hạn bởi đường cong $y = (x – 2){e^x}$, trục hoành và trục tung. Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng $pi left( {frac{{{e^4}}}{a} + frac{b}{4}} right)$ với $a$, $b$ là các số nguyên. Điểm $I(a;b)$ là tâm đối xứng của đồ thị hàm số nào sau đây?
A. $y = frac{{10x + 2016}}{{x – 4}}.$
B. $y = frac{{11x + 2017}}{{2 – x}}.$
C. $y = frac{{12x + 2018}}{{4 – x}}.$
D. $y = frac{{13x + 2019}}{{4 – x}}.$Lời giải:
Hoành độ giao điểm: $(x – 2){e^x} = 0$ $ Leftrightarrow x = 2.$
Thể tích: $V = pi int_0^2 {{{(x – 2)}^2}} {e^{2x}}dx.$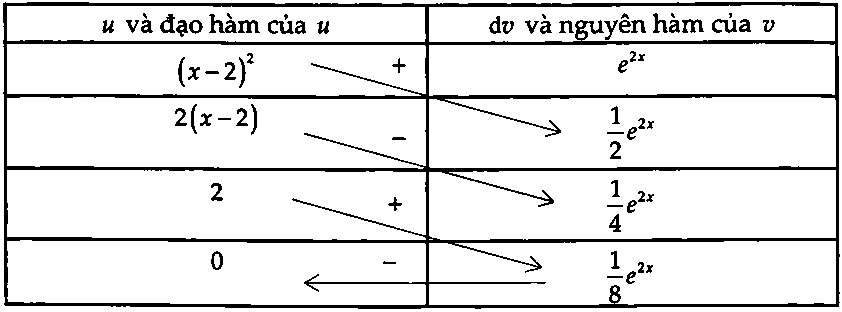 $V = left. {pi left[ {frac{{{{(x – 2)}^2}{e^{2x}}}}{2} – frac{{(x – 2){e^{2x}}}}{2} + frac{{{e^{2x}}}}{4}} right]} right|_0^2$ $ = pi left( {frac{{{e^4}}}{4} – frac{{13}}{4}} right)$ $ Rightarrow a = 4$, $b = – 13.$
$V = left. {pi left[ {frac{{{{(x – 2)}^2}{e^{2x}}}}{2} – frac{{(x – 2){e^{2x}}}}{2} + frac{{{e^{2x}}}}{4}} right]} right|_0^2$ $ = pi left( {frac{{{e^4}}}{4} – frac{{13}}{4}} right)$ $ Rightarrow a = 4$, $b = – 13.$
$ Rightarrow I(4; – 13)$ là tâm đối xứng của đồ thị hàm số $y = frac{{13x + 2019}}{{4 – x}}.$
Chọn đáp án D.Ví dụ 26: Cho hình phẳng $D$ giới hạn bởi đường cong $y = sqrt {frac{{ln x}}{x}} $, trục hoành và các đường thẳng $x = 1$, $x = {e^2}.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng:
A. $1.$
B. $2.$
C. $3.$
D. $4.$Lời giải:
$V = pi int_1^{{e^2}} {frac{{ln x}}{x}dx} $ $ = pi int_1^{{e^2}} {ln xd(ln x)} $ $ = left. {frac{{{{ln }^2}x}}{2}} right|_1^{{e^2}} = 2.$
Chọn đáp án B.Ví dụ 27: Cho hình phẳng $D$ giới hạn bởi đường cong $y = sqrt {(2x – 2)ln x} $, trục hoành và đường thẳng $x=2.$ Khối tròn xoay tạo thành khi quay $D$ quanh trục hoành có thể tích bằng $frac{a}{b}pi $ với $a$ là số nguyên dương, $frac{a}{b}$ là phân số tối giản. Tính $T = ln {a^{2018}} + b.$
A. $2.$
B. $3.$
C. $2020.$
D. $2021.$Lời giải:
Hoành độ giao điểm: $sqrt {(2x – 2)ln x} = 0$ $ Leftrightarrow x = 1.$
Thể tích: $V = pi int_1^2 {(2x – 2)} ln xdx.$
Đặt $left{ {begin{array}{*{20}{l}}
{u = ln x}\
{dv = (2x – 2)dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{1}{x}dx}\
{v = {x^2} – 2x}
end{array}} right..$
$V = pi left[ {left. {left( {{x^2} – 2x} right)ln x} right|_1^2 – int_1^2 {(x – 2)dx} } right]$ $ = pi left[ {left. {left( {{x^2} – 2x} right)ln x} right|_1^2 – left. {left( {frac{{{x^2}}}{2} – 2x} right)} right|_1^2} right]$ $ = frac{pi }{2}.$
$ Rightarrow a = 1$, $b = 2$ $ Rightarrow T = ln {a^{2018}} + b = 2.$
Chọn đáp án A.III. LUYỆN TẬP
1. ĐỀ BÀI
Câu 1: Cho thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = 3x – {x^2}$, $y = 0$ quanh trục $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $T= a+2b.$
A. $T = 172.$
B. $T=101.$
C. $T=20.$
D. $T=13.$Câu 2: Cho thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = 2x – {x^2}$, $y = 0$ quanh trục $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Giá trị $2a+b$ thuộc khoảng nào sau đây?
A. $(10;12).$
B. $(12;14).$
C. $(44;47).$
D. $(46;48).$Câu 3: Cho thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = sin x$, $y = 0$, $x = 0$, $x = pi $ quanh trục $Ox$ bằng $frac{a}{b}{pi ^2}$ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Khẳng định nào sau đây là đúng?
A. $a>b.$
B. $a<b.$
C. $a=b+3.$
D. $b=a+2.$Câu 4: Cho thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = sqrt {frac{x}{{4 – {x^2}}}} $, $y = 0$, $x = 1$ quanh trục $Ox$ bằng $frac{pi }{a}ln frac{b}{c}$ với $b$, $c$ là các số nguyên dương và $frac{b}{c}$ là phân số tối giản. Tính $T = a+b-c.$
A. $T=1.$
B. $T=3.$
C. $T=4.$
D. $T=5.$Câu 5: Cho thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = sqrt {{e^x}} $, $y = 0$, $x = 0$, $x = 1$ quanh trục $Ox$ bằng $pi (ae + b)$ với $a$, $b$ là các số nguyên. Tính $T=5a+b.$
A. $T=-4.$
B. $T=-2.$
C. $T=2.$
D. $T=4.$ Câu 6: Cho thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = sqrt {{{sin }^4}x + {{cos }^4}x} $, $y = 0$, $x = frac{pi }{2}$, $x = pi $ quanh trục $Ox$ bằng $frac{a}{b}{pi ^2}$ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính độ dài đoạn thẳng $OA$ với $A(a;b).$
A. $OA = sqrt {71} .$
B. $OA = sqrt {72} .$
C. $OA = sqrt {73} .$
D. $OA = sqrt {74} .$Câu 7: Cho thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = sqrt {xsin x} $, $y = 0$, $x = 0$, $x = pi $ quanh trục $Ox$ bằng $a{pi ^2}.$ Tính khoảng cách $h$ từ điểm $A(1;a)$ đến đường thẳng $Delta :3x + 4y – 1 = 0.$
A. ${h = frac{6}{5}.}$
B. ${h = frac{7}{5}.}$
C. ${h = frac{8}{5}.}$
D. ${h = frac{9}{5}}.$Câu 8: Cho thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = sqrt {frac{{1 – x}}{x}} $ $(0 < x le 1)$, $y = 0$, $x = frac{1}{2}$ quanh trục $Ox$ bằng $V = pi left( {ln 2 + frac{a}{b}} right)$ với $b$ là số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $T=2a+b.$
A. $T=0.$
B. $T=3.$
C. $T=5.$
D. $T=7.$ Câu 9: Cho thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = x{e^x}$, $y = 0$, $x = 0$, $x = 2$ quanh trục $Ox$ bằng $frac{pi }{4}left( {a{e^4} + b} right).$ Tính $T= a + 2b.$
A. $T=1.$
B. $T =3.$
C. $T = 5.$
D. $T=9.$Câu 10: Cho thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $y = sqrt {3 – cos x} $, $y = 0$, $x = 0$, $x = frac{pi }{6}$ quanh trục $Ox$ bằng $frac{{pi (pi – 1)}}{a}.$ Tính $T = {log _2}a.$
A. $T=0.$
B. $T=1.$
C. $T=2.$
D. $T =3.$2. BẢNG ĐÁP ÁN

Be the first to comment