
Bài viết trình bày lý thuyết cơ bản về số phức và các phép toán trên tập số phức, các kiến thức trong bài viết được tham khảo từ .I. Số phức
Số $i$: Việc xây dựng tập hợp số phức được đặt ra từ việc mở rộng tập hợp số thực sao cho mọi phương trình đa thức đều có nghiệm. Để giải quyết vấn đề này, ta bổ sung vào tập số thực $R$ một số mới, kí hiệu là $i$ và coi nó là một nghiệm của phương trình ${x^2} + 1 = 0$, như vậy ${i^2} = -1$.
1. Định nghĩa
Mỗi biểu thức dạng $a + bi$, trong đó $a,b in R, {i^2} = – 1$ được gọi là một số phức.
Đối với số phức $z = a + bi$, ta nói $a$ là phần thực, $b$ là phần ảo của $z.$
Tập hợp các số phức kí hiệu là $C.$
2. Số phức bằng nhau
Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau.
$a + bi = c + di Leftrightarrow a = c.$
Nhận xét:
1. Từ sự bằng nhau của số phức, ta suy ra mỗi số phức được hoàn toàn được xác định bởi một cặp số thực. Đây là cơ sở cho phần 3: biểu diễn hình học của số phức.
2. Mỗi số thực $a$ được đồng nhất với số phức $a + 0i$, nên mỗi số thực cũng là một số phức. Do đó, tập số thực $R$ là tập con của tập số phức $C.$
3. Số phức $0 + bi$ được gọi là số thuần ảo và được viết đơn giản là $bi$.
4. Số $i$ được gọi là đơn vị ảo.
3. Biểu diễn hình học của số phức
Điểm biểu diễn số phức $z = a + bi$ trên mặt phẳng tọa độ là điểm $Mleft( {a;b} right).$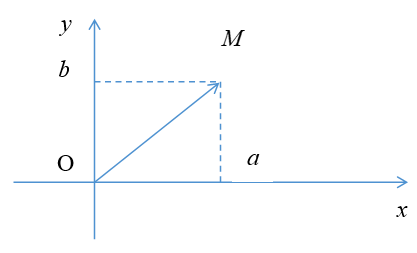 4. Mô đun số phức
4. Mô đun số phức
Giả sử số phức $z = a + bi$ được biểu diễn bởi điểm $Mleft( {a;b} right)$ trên mặt phẳng tọa độ. Khi đó, độ dài của vectơ $overrightarrow {OM} $ được gọi là mô đun của số phức $z$ và được kí hiệu là $left| z right|$. Vậy $left| z right| = left| {overrightarrow {OM} } right| = sqrt {{a^2} + {b^2}}$.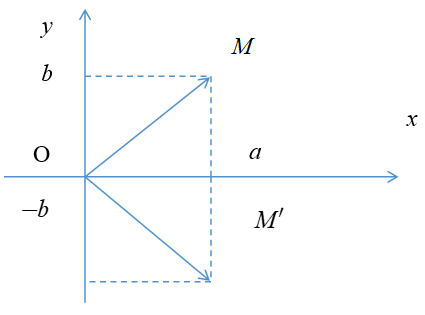 5. Số phức liên hợp
5. Số phức liên hợp
Cho số phức $z = a + bi$. Ta gọi $z = a – bi$ là số phức liên hợp của $z$ và kí hiệu là $bar z = a – bi$.
Chú ý:
1. Tổng của một số phức với số phức liên hợp của nó nó bằng hai lần phần thực của số phức đó.
2. Tích của một số phức với số phức liên hợp của nó nó bằng bình phương mô đun của số phức đó.
[ads]
II. Các phép toán với số phức
1. Phép cộng và phép trừ
Quy tắc: Để cộng (trừ) hai số phức, ta cộng (trừ) hai phần thực và hai phần ảo của chúng.
1. $left( {a + bi} right) + left( {c + di} right) = left( {a + c} right) + left( {b + d} right)i.$
2. $left( {a + bi} right) – left( {c + di} right) = left( {a – c} right) + left( {b – d} right)i.$
2. Phép nhân và phép chia
a. Phép nhân
Phép nhân hai số phức được thực hiện theo quy tắc nhân đa thức rồi thay ${i^2} = – 1$ trong kết quả nhận được.
${left( {a + bi} right)left( {c + di} right) = left( {ac – bd} right) + left( {ad + bc} right)i}.$
b. Phép chia
Quy tắc thực hiện phép chia hai số phức: “Thực hiện phép chia $frac{{c + di}}{{a + bi}}$ là nhân cả tử và mẫu với số phức liên hợp của $a + bi$”.
$frac{{c + di}}{{a + bi}} = frac{{left( {c + di} right)left( {a – bi} right)}}{{{a^2} – {b^2}{i^2}}}$ $ = frac{{ac + bd}}{{{a^2} + {b^2}}} + frac{{ad – bc}}{{{a^2} + {b^2}}}i.$
3. Phương trình bậc hai với hệ số thực
Các căn bậc hai của số thực $a < 0$ là $ pm isqrt {left| a right|}$.
Xét phương trình bậc hai $a{x^2} + bx + c = 0$ với $a,b,c in R, a ne 0$. Xét biệt số $Delta = {b^2} – 4ac$, ta có:
+ $Delta = 0$: Phương trình có một nghiệm thực $x = – frac{b}{{2a}}$.
+ $Delta > 0$: Phương trình có hai nghiệm thực phân biệt được xác định bởi công thức ${x_{1,2}} = frac{{ – b pm sqrt Delta }}{{2a}}$.
+ $Delta < 0$:
1. Nếu xét trên tập số thực thì phương trình vô nghiệm.
2. Nếu xét trên tập số phức thì phương trình có hai nghiệm phức được xác định bởi công thức ${x_{1,2}} = frac{{ – b pm isqrt {left| Delta right|} }}{{2a}}$.

Be the first to comment