Bài viết hướng dẫn phương pháp tìm tập xác định của hàm số lượng giác, đây là dạng toán cơ bản mà học sinh cần nắm vững trước khi tìm hiểu các phương pháp giải phương trình lượng giác.PHƯƠNG PHÁP: Để tìm tìm tập xác định của hàm số lượng giác, ta sử dụng một trong các cách sau:
Cách 1: Tìm tập $D$ của $x$ để $fleft( x right)$ có nghĩa, tức là tìm ${rm{D}} = left{ {x in Rleft| {fleft( x right) in R} right.} right}.$
Cách 2: Tìm tập $E$ của $x$ để $fleft( x right)$ không có nghĩa, khi đó tập xác định của hàm số là ${rm{D}} = Rbackslash E.$CHÚ Ý:
A. Với hàm số $fleft( x right)$ cho bởi biểu thức đại số thì ta có:
1. $fleft( x right) = frac{{{f_1}left( x right)}}{{{f_2}left( x right)}}$, điều kiện: ${f_1}left( x right)$ có nghĩa, ${f_2}left( x right)$ có nghĩa và ${f_2}left( x right) ne 0$.
2. $fleft( x right) = sqrt[{2m}]{{{f_1}left( x right)}},left( {m in N} right)$, điều kiện: ${f_1}left( x right)$ có nghĩa và ${f_1}left( x right) ge 0.$
3. $fleft( x right) = frac{{{f_1}left( x right)}}{{sqrt[{2m}]{{{f_2}left( x right)}}}},left( {m in N} right)$, điều kiện: ${f_1}left( x right), {f_2}left( x right)$ có nghĩa và ${f_2}left( x right) > 0.$
B. Hàm số $y = sin x;y = cos x$ xác định trên $R$, như vậy:
1. $y = sin left[ {uleft( x right)} right]$; $y = cos left[ {uleft( x right)} right]$ xác định khi và chỉ khi $uleft( x right)$ xác định.
2. $y = tan left[ {uleft( x right)} right]$ có nghĩa khi và chỉ khi $uleft( x right)$ xác định và $uleft( x right) ne frac{pi }{2} + kpi ;k in Z.$
3. $y = cot left[ {uleft( x right)} right]$ có nghĩa khi và chỉ khi $uleft( x right)$ xác định và $uleft( x right) ne + kpi ;k in Z.$Ở phần này chúng ta chỉ cần nhớ kĩ điều kiện xác định của các hàm số cơ bản như sau:
1. Hàm số $y = sin x$ và $y = cos x$ xác định trên $R.$
2. Hàm số $y = tan x$ xác định trên $Rbackslash left{ {frac{pi }{2} + kpi left| {k in Z} right.} right}.$
3. Hàm số $y = cot x$ xác định trên $Rbackslash left{ {kpi left| {k in Z} right.} right}.$Ví dụ 1: Tìm tập xác định của hàm số $y = frac{1}{{2cos x – 1}}.$Hàm số đã cho xác định khi $2cos x – 1 ne 0$ $ Leftrightarrow left{ begin{array}{l}
cos x ne cos frac{pi }{3}\
cos x ne cos frac{{5pi }}{3}
end{array} right.$ $ Leftrightarrow left{ begin{array}{l}
x ne frac{pi }{3} + k2pi \
x ne frac{{5pi }}{3} + k2pi
end{array} right.$ $k in Z.$Ví dụ 2: Tìm tập xác định của hàm số $y = frac{{cot x}}{{sin x – 1}}.$Hàm số đã cho xác định khi:
+ $cot x$ xác định $ Leftrightarrow sin x ne 0.$
+ $sin x – 1 ne 0$
$ Leftrightarrow left{ begin{array}{l}
sin x ne 0\
sin x ne 1
end{array} right.$ $ Leftrightarrow left{ begin{array}{l}
x ne kpi \
x ne frac{pi }{2} + k2pi
end{array} right.$ $(k in Z).$Ví dụ 3: Tìm tập xác định của hàm số $y = 2016{tan ^{2017}}2x.$Ta có $y = 2016{tan ^{2017}}2x$ $ = 2016.{left( {tan 2x} right)^{2017}}.$
2017 là một số nguyên dương, do vậy hàm số đã cho xác định khi $tan 2x$ xác định $ Leftrightarrow 2x ne frac{pi }{2} + kpi ,,k in Z$ $ Leftrightarrow x ne frac{pi }{4} + kfrac{pi }{2},,k in Z.$
[ads]
Dạng toán chứa tham số trong bài toán liên quan đến tập xác định của hàm số lượng giác
Khi giải dạng toán này, ta cần lưu ý: Với $S subset {D_f}$ ($D_f$ là tập xác định của hàm số $f(x)$) thì:
+ ${rm{ }}fleft( x right) le m,forall x in S$ $ Leftrightarrow mathop {max }limits_S fleft( x right) le m$
+ $fleft( x right) ge m,forall x in S$ $ Leftrightarrow mathop {min }limits_S fleft( x right) ge m$
+ $exists {x_0} in S,fleft( {{x_0}} right) le m$ $ Leftrightarrow mathop {min }limits_S fleft( x right) le m$
+ $exists {x_0} in S,fleft( {{x_0}} right) ge m$ $ Leftrightarrow mathop {max }limits_S fleft( x right) ge m$Ví dụ 4: Cho hàm số $hleft( x right) $ $= sqrt {{{sin }^4}x + {{cos }^4}x – 2msin x.cos x} $. Tìm tất cả các giá trị của tham số $m$ để hàm số xác định với mọi số thực $x$ (trên toàn trục số).Xét hàm số $gleft( x right) $ $= {left( {{{sin }^2}x} right)^2} + {left( {{{cos }^2}x} right)^2} – msin 2x$
$ = {left( {{{sin }^2}x + {{cos }^2}x} right)^2}$ $ – 2{sin ^2}x{cos ^2}x – msin 2x$
$ = 1 – frac{1}{2}{sin ^2}2x – msin 2x .$
Đặt $t = sin 2x$ $ Rightarrow t in left[ { – 1;1} right]$.
Hàm số $hleft( x right)$ xác định với mọi $x in R$ $ Leftrightarrow gleft( x right) ge 0,forall x in R$ $ Leftrightarrow – frac{1}{2}{t^2} – mt + 1 ge 0$ $forall t in left[ { – 1;1} right]$ $ Leftrightarrow {t^2} + 2mt – 2 le 0$ $forall t in left[ { – 1;1} right].$
Đặt $fleft( t right) = {t^2} + 2mt – 2$ trên $left[ { – 1;1} right].$
Đồ thị hàm số có thể là một trong ba đồ thị dưới đây: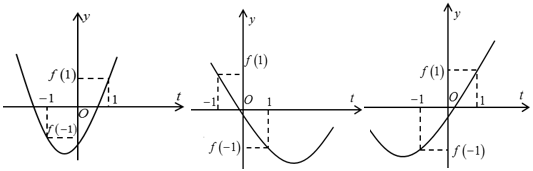
Ta thấy $mathop {max }limits_{left[ { – 1;1} right]} fleft( t right) = fleft( 1 right)$ hoặc $mathop {max }limits_{left[ { – 1;1} right]} fleft( t right) = fleft( { – 1} right).$
Do đó: $fleft( t right) = {t^2} + 2mt – 2 le 0$ $forall t in left[ { – 1;1} right]$ $ Leftrightarrow mathop {max }limits_{left[ { – 1;1} right]} fleft( t right) le 0$ $ Leftrightarrow left[ begin{array}{l}
fleft( 1 right) le 0\
fleft( { – 1} right) le 0
end{array} right.$
$ Leftrightarrow left[ begin{array}{l}
– 1 + 2m le 0\
– 1 – 2m le 0
end{array} right.$ $ Leftrightarrow – frac{1}{2} le m le frac{1}{2}.$Ví dụ 5: Tìm $m$ để hàm số $y = frac{{3x}}{{sqrt {2{{sin }^2}x – msin x + 1} }}$ xác định trên $R.$Hàm số xác định trên $R$ khi và chỉ khi $2{sin ^2}x – msin x + 1 > 0$ $forall x in R.$
Đặt $t = sin x$ $ Rightarrow t in left[ { – 1;1} right].$ Lúc này ta đi tìm điều kiện của $m$ để $fleft( t right) = 2{t^2} – mt + 1 > 0$ $forall t in left[ { – 1;1} right].$
Ta có ${Delta _t} = {m^2} – 8.$
+ Trường hợp 1: ${Delta _t} < 0 Leftrightarrow {m^2} – 8 < 0$ $ Leftrightarrow – 2sqrt 2 < m < 2sqrt 2 .$ Khi đó $fleft( t right) > 0$ $forall t$ (thỏa mãn).
+ Trường hợp 2: ${Delta _t} = 0 Leftrightarrow {m^2} – 8 = 0$ $ Leftrightarrow left[ begin{array}{l}
m = – 2sqrt 2 \
m = 2sqrt 2
end{array} right.$ (thử lại thì cả hai trường hợp đều không thỏa mãn).
+ Trường hợp 3: ${Delta _t} > 0 Leftrightarrow {m^2} – 8 > 0$ $ Leftrightarrow left[ begin{array}{l}
m < – 2sqrt 2 \
m > 2sqrt 2
end{array} right.$ khi đó tam thức $fleft( t right) = 2{t^2} – mt + 1$ có hai nghiệm phân biệt ${t_1}; {t_2} left( {{t_1} < {t_2}} right).$
Để $fleft( t right) > 0,forall t in left[ { – 1;1} right]$ thì: $left[ begin{array}{l}
{t_1} ge 1 Leftrightarrow frac{{m – sqrt {{m^2} – 8} }}{4} ge 1\
{t_2} le – 1 Leftrightarrow frac{{m + sqrt {{m^2} – 8} }}{4} le – 1
end{array} right.$ $ Leftrightarrow left[ begin{array}{l}
sqrt {{m^2} – 8} ge m – 4left( {VN} right)\
sqrt {{m^2} – 8} le – m – 4left( {VN} right)
end{array} right.$
Vậy $m in left( { – 2sqrt 2 ;2sqrt 2 } right)$ thỏa mãn yêu cầu bài toán.
Be the first to comment