
Bài viết hướng dẫn phương pháp giải bài toán ứng dụng của tích phân để tính diện tích hình phẳng giới hạn bởi một đường cong và trục hoành.I. KIẾN THỨC CẦN NHỚ
1. Cho hàm số $y = f(x)$ liên tục trên đoạn $[a;b].$ Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$, trục hoành và hai đường thẳng $x = a$, $x = b$ là: $S = int_a^b {left| {f(x)} right|dx} .$
2. Học sinh cần xem lại cách khử dấu giá trị tuyệt đối trong công thức tính diện tích hình phẳng.
3. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$ và trục hoành cho bởi công thức $S = int_alpha ^beta {left| {f(x)} right|dx} $, trong đó $alpha $, $beta $ lần lượt là nghiệm nhỏ nhất và lớn nhất của phương trình $f(x) = 0.$II. BÀI TẬP TRẮC NGHIỆM MINH HỌA
Ví dụ 1: Gọi $S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$, trục hoành và hai đường thẳng $x=a$, $x=b$ (phần gạch chéo trong hình vẽ bên).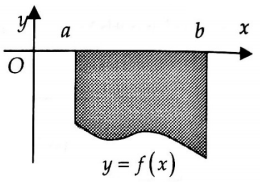 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
A. $S = int_b^a {left| {f(x)} right|dx} .$
B. $S = int_a^b {f(x)dx} .$
C. $S = – int_a^b {f(x)dx} .$
D. $S = – int_b^a {f(x)dx} .$Lời giải:
Từ đồ thị ta có $f(x) < 0$, $forall x in [a;b]$ $ Rightarrow S = int_a^b {left| {f(x)} right|dx} $ $ = – int_a^b {f(x)dx} .$
Chọn đáp án C.Ví dụ 2: Gọi $S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$, trục hoành và hai đường thẳng $x=a$, $x=b$ (phần gạch chéo trong hình vẽ bên).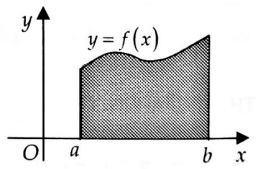 Khẳng định nào sau đây sai?
Khẳng định nào sau đây sai?
A. $S = int_a^b {left| {f(x)} right|dx} .$
B. $S = – int_b^a {f(x)dx} .$
C. $S = left| {int_b^a {f(x)dx} } right|.$
D. $S = int_b^a {f(x)dx} .$Lời giải:
Từ đồ thị ta có $f(x) > 0$, $forall x in [a;b]$ nên:
$S = int_a^b {left| {f(x)} right|dx} $ $ = left| {int_a^b {f(x)dx} } right|$ $ = left| { – int_b^a {f(x)dx} } right|$ $ = left| {int_b^a {f(x)dx} } right|.$
Suy ra các đáp án A và C đúng.
$S = int_a^b f (x)dx$ $ = – int_b^a f (x)dx$, suy ra đáp án B đúng và đáp án D sai.
Chọn đáp án D.Ví dụ 3: Gọi $S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$, trục hoành và hai đường thẳng $x= a$, $x=b$ (phần gạch chéo trong hình vẽ bên).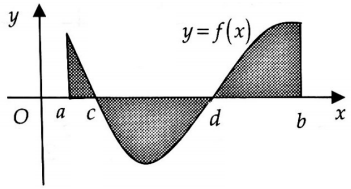 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
A. $S = left| {int_a^b f (x)dx} right|.$
B. $S = int_a^c f (x)dx – int_c^d f (x)dx + int_d^b f (x)dx.$
C. $S = int_a^c | f(x)|dx – int_c^d | f(x)|dx + int_d^b | f(x)|dx.$
D. $S = left| {int_a^c f (x)dx} right| – left| {int_c^d f (x)dx} right| + left| {int_d^b f (x)dx} right|.$Lời giải:
Từ đồ thị ta có: $f(x) ge 0$, $forall x in [a;c]$; $f(x) le 0$, $forall x in [c;d]$; $f(x) ge 0$, $forall x in [d;b].$
Suy ra $S = int_a^b | f(x)|dx$ $ = int_a^c | f(x)|dx$ $ + int_c^d | f(x)|dx$ $ + int_d^b | f(x)|dx.$
$ = int_a^c f (x)dx$ $ – int_c^d f (x)dx$ $ + int_d^b f (x)dx.$
Chọn đáp án B.Ví dụ 4: Tính diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y = {x^2} + 3x$, $Ox$ và hai đường thẳng $x=1$, $x=2.$
A. $S = frac{{41}}{6}.$
B. $S = frac{{43}}{6}.$
C. $S = frac{{47}}{6}.$
D. $S = frac{{53}}{6}.$Lời giải:
Cách 1:
Ta có: $S = int_1^2 {left| {{x^2} + 3x} right|dx} .$
Bảng xét dấu: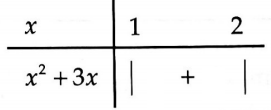 Suy ra $S = int_1^2 {left( {{x^2} + 3x} right)dx} $ $ = left. {left( {frac{{{x^3}}}{3} + frac{{3{x^2}}}{2}} right)} right|_1^2$ $ = frac{{41}}{6}.$
Suy ra $S = int_1^2 {left( {{x^2} + 3x} right)dx} $ $ = left. {left( {frac{{{x^3}}}{3} + frac{{3{x^2}}}{2}} right)} right|_1^2$ $ = frac{{41}}{6}.$
Chọn đáp án A.
Cách 2:
Xét phương trình ${x^2} + 3x = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 0 notin [1;2]}\
{x = – 3 notin [1;2]}
end{array}} right..$
Do đó: $S = int_1^2 {left| {{x^2} + 3x} right|dx} $ $ = left| {int_1^2 {left( {{x^2} + 3x} right)dx} } right|$ $left| {left. {left( {frac{{{x^3}}}{3} + frac{{3{x^2}}}{2}} right)} right|_1^2} right|$ $ = frac{{41}}{6}.$
Cách 3:
Vẽ đồ thị ta được hình phẳng giới hạn bởi đồ thị hàm số $y = {x^2} + 3x$, $Ox$ và hai đường thẳng $x=1$, $x=2$ như hình bên.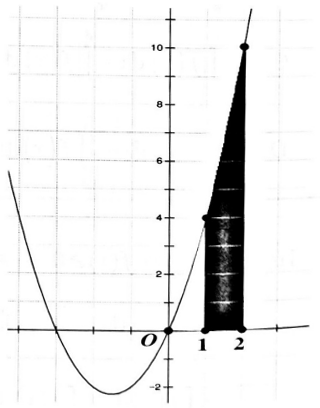 Do đó: $S = int_1^2 {left( {{x^2} + 3x} right)dx} $ $ = left. {left( {frac{{{x^3}}}{3} + frac{{3{x^2}}}{2}} right)} right|_1^2 = frac{{41}}{6}.$Ví dụ 5: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = {x^2} – x – 2$ và trục hoành bằng $frac{a}{b}$, với $frac{a}{b}$ là phân số tối giản. Khẳng định nào sau đây đúng?
Do đó: $S = int_1^2 {left( {{x^2} + 3x} right)dx} $ $ = left. {left( {frac{{{x^3}}}{3} + frac{{3{x^2}}}{2}} right)} right|_1^2 = frac{{41}}{6}.$Ví dụ 5: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = {x^2} – x – 2$ và trục hoành bằng $frac{a}{b}$, với $frac{a}{b}$ là phân số tối giản. Khẳng định nào sau đây đúng?
A. $a le b.$
B. $a = {b^2} + 1.$
C. $a > b + 10.$
D. $a = b + 7.$Lời giải:
Xét phương trình ${x^2} – x – 2 = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = – 1}\
{x = 2}
end{array}} right..$
Do đó $S = int_{ – 1}^2 {left| {{x^2} – x – 2} right|dx} $ $ = left| {int_{ – 1}^2 {left( {{x^2} – x – 2} right)dx} } right|$ $left| {left. {left( {frac{{{x^3}}}{3} – frac{{{x^2}}}{2} – 2x} right)} right|_{ – 1}^2} right| = frac{9}{2}.$
Suy ra $a = 9$, $b = 2$ $ Rightarrow a = b + 7.$
Chọn đáp án D.Ví dụ 6: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = {x^3} – x$ và trục hoành bằng $frac{a}{b}$, với $frac{a}{b}$ là phân số tối giản. Tính $I = 2a + 5b.$
A. $I = 11.$
B. $I = 12.$
C. $I = 13.$
D. $I = 14.$Lời giải:
Xét phương trình ${x^3} – x = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 0}\
{x = pm 1}
end{array}} right..$
Do đó $S = int_{ – 1}^1 {left| {{x^3} – x} right|dx} $ $ = left| {int_{ – 1}^0 {left( {{x^3} – x} right)dx} } right|$ $ + left| {int_0^1 {left( {{x^3} – x} right)dx} } right|.$
$ = left| {left. {left( {frac{{{x^4}}}{4} – frac{{{x^2}}}{2}} right)} right|_{ – 1}^0} right|$ $ + left| {left. {left( {frac{{{x^4}}}{4} – frac{{{x^2}}}{2}} right)} right|_0^1} right|$ $ = frac{1}{2}.$
Suy ra $a = 1$, $b = 2$ $ Rightarrow I = 2a + 5b = 12.$
Chọn đáp án B.Ví dụ 7: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = 2{x^2} – {x^4}$ và trục hoành bằng $frac{a}{b}sqrt 2 $ với $frac{a}{b}$ là phân số tối giản. Tính $T = a – b.$
A. $T=-7.$
B. $T=1.$
C. $T=4.$
D. $T = 2.$Lời giải:
Xét phương trình $2{x^2} – {x^4} = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 0}\
{x = pm sqrt 2 }
end{array}} right..$
Do đó $S = int_{ – sqrt 2 }^{sqrt 2 } {left| {2{x^2} – {x^4}} right|dx} $ $ = left| {int_{ – sqrt 2 }^0 {left( {2{x^2} – {x^4}} right)dx} } right|$ $ + left| {int_0^{sqrt 2 } {left( {2{x^2} – {x^4}} right)dx} } right|.$
$ = left| {left. {left( {frac{{2{x^3}}}{3} – frac{{{x^4}}}{4}} right)} right|_{ – sqrt 2 }^0} right|$ $ + left| {left. {left( {frac{{2{x^3}}}{3} – frac{{{x^4}}}{4}} right)} right|_0^{sqrt 2 }} right|$ $ = frac{{16sqrt 2 }}{{15}}.$
Suy ra $a = 16$, $b = 15$ $ Rightarrow T = a – b = 1.$
Chọn đáp án B.Ví dụ 8: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = {e^x} – 2$, trục hoành và đường thẳng $x=1$ bằng $a.e + b + c.ln 2$ với $a$, $b$, $c$ là các số nguyên. Tính $T = 2{a^{2018}} + b + {c^2}.$
A. $T=0.$
B. $T=1.$
C. $T=2.$
D. $T=3.$Lời giải:
Xét phương trình ${e^x} – 2 = 0$ $ Leftrightarrow x = ln 2.$
Do đó $S = int_{ln 2}^1 {left| {{e^x} – 2} right|dx} $ $ = left| {int_{ln 2}^1 {left( {{e^x} – 2} right)dx} } right|$ $ = left| {left. {left( {{e^x} – 2x} right)} right|_{ln 2}^1} right|$ $ = e – 4 + 2ln 2.$
Suy ra $a = 1$, $b = – 4$, $c = 2$ $ Rightarrow T = 2{a^{2018}} + b + {c^2} = 2.$
Chọn đáp án C.Ví dụ 9: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = sin x + cos x – 2$, trục hoành, trục trung và đường thẳng $x = frac{pi }{2}$ bằng $a + bpi $ với $a$, $b$ là các số nguyên. Tính $T = 2a + 3b.$
A. $T=-4.$
B. $T=-1.$
C. $T=7.$
D. $T =8.$Lời giải:
Ta có $y = sin x + cos x – 2 < 0$, $forall x in left[ {0;frac{pi }{2}} right].$
Do đó $S = int_0^{frac{pi }{2}} | sin x + cos x – 2|dx$ $ = int_0^{frac{pi }{2}} {(2 – sin x – cos )dx} .$
$ = left. {(2x + cos x – sin x)} right|_0^{frac{pi }{2}}$ $ = pi – 2.$
Suy ra $a = – 2$, $b = 1$ $ Rightarrow T = 2a + 3b = – 1.$
Chọn đáp án B.Ví dụ 10: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = x{e^x} – {e^x}$, trục hoành và trục tung bằng $a + be$ với $a$, $b$ là các số nguyên. Tính $T = 5a + b.$
A. $T = 11.$
B. $T = 7.$
C. $T=3.$
D. $T=-9.$Lời giải:
Xét phương trình $x{e^x} – {e^x} = 0$ $ Leftrightarrow x = 1.$
Do đó $S = int_0^1 {left| {x{e^x} – {e^x}} right|dx} $ $ = left| {int_0^1 {(x – 1){e^x}dx} } right|.$
Sử dụng bảng: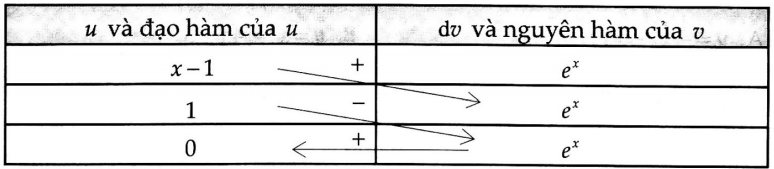 $ Rightarrow S = left| {left. {(x – 1){e^x}} right|_0^1 – left. {{e^x}} right|_0^1} right|$ $ = e – 2$ $ Rightarrow a = – 2$, $b = 1$ $ Rightarrow T = 5a + b = – 9.$
$ Rightarrow S = left| {left. {(x – 1){e^x}} right|_0^1 – left. {{e^x}} right|_0^1} right|$ $ = e – 2$ $ Rightarrow a = – 2$, $b = 1$ $ Rightarrow T = 5a + b = – 9.$
Chọn đáp án D.Ví dụ 11: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = xln x$, trục hoành và đường thẳng $x=2$ bằng $a + bln 2$ với $a$, $b$ là các số hữu tỉ. Tính $T = 2a + b.$
A. $T = frac{7}{2}.$
B. $T = frac{{13}}{4}.$
C. $T = frac{{19}}{4}.$
D. $T = frac{1}{2}.$Lời giải:
Xét phương trình $xln x = 0$ $ Leftrightarrow x = 1.$
Do đó $S = int_1^2 {|xln x|dx} $ $ = left| {int_1^2 {xln xdx} } right|.$
Đặt $left{ {begin{array}{*{20}{l}}
{u = ln x}\
{dv = xdx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{1}{x}dx}\
{v = frac{{{x^2}}}{2}}
end{array}} right..$
$S = left| {left. {frac{{{x^2}}}{2}ln x} right|_1^2 – int_1^2 {frac{x}{2}dx} } right|$ $ = left| {left. {frac{{{x^2}}}{2}ln x} right|_1^2 – left. {frac{{{x^2}}}{4}} right|_1^2} right|$ $ = 2ln 2 – frac{3}{4}.$
Suy ra $a = – frac{3}{4}$, $b = 2$ $ Rightarrow T = 2a + b = frac{1}{2}.$
Chọn đáp án D.Ví dụ 12: Cho diện tích của hình phẳng giới hạn bởi các đường $x = 1$, $x = e$, $y = 0$, $y = frac{{ln x}}{{2sqrt x }}$ bằng $a + bsqrt e $ với $a$, $b$ là các số nguyên. Điểm $M(a;b)$ là đỉnh của parabol nào sau đây?
A. $y = frac{1}{2}{x^2} – x.$
B. $y = {x^2} – 4x + 3.$
C. $y = {x^2} + x – 7.$
D. $y = – {x^2} + 2x – 1.$Lời giải:
Ta có $y = frac{{ln x}}{{2sqrt x }} ge 0$, $forall x in [1;e].$
Do đó $S = int_1^e {left| {frac{{ln x}}{{2sqrt x }}} right|dx} $ $ = int_1^e {frac{{ln x}}{{2sqrt x }}dx} .$
Đặt $left{ {begin{array}{*{20}{l}}
{u = ln x}\
{dv = frac{1}{{2sqrt x }}dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{1}{x}dx}\
{v = sqrt x }
end{array}} right..$
$S = left. {sqrt x ln x} right|_1^e – int_1^e {frac{1}{{sqrt x }}dx} $ $ = left. {sqrt x ln x} right|_1^e – left. {2sqrt x } right|_1^e$ $ = 2 – sqrt e .$
Suy ra $a = 2$, $b = – 1$ $ Rightarrow M(2; – 1).$
Suy ra $M(2; – 1)$ là đỉnh của parabol $y = {x^2} – 4x + 3.$
Chọn đáp án B.Ví dụ 13: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = x(2 + sin x)$, trục hoành và đường thẳng $x = frac{pi }{2}$ bằng $a + frac{{{pi ^2}}}{b}$ với $a$, $b$ là các số nguyên. Tính $T = {a^2} – 2b.$
A. $T = 14.$
B. $T = – frac{{31}}{{16}}.$
C. $T = – 7.$
D. $T = frac{7}{8}.$Lời giải:
Xét phương trình $x(2 + sin x) = 0$ $ Leftrightarrow x = 0.$
Do đó $S = int_0^{frac{pi }{2}} {|x(2 + sin x)|dx} $ $ = int_0^{frac{pi }{2}} x (2 + sin x)dx$ (vì $x(2 + sin x) ge 0$, $forall x in left[ {0;frac{pi }{2}} right]$).
Đặt $left{ {begin{array}{*{20}{l}}
{u = x}\
{dv = (2 + sin x)dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = dx}\
{v = 2x – cos x}
end{array}} right..$
$S = left. {x(2x – cos x)} right|_0^{frac{pi }{2}}$ $ – int_0^{frac{pi }{2}} {(2x – cos x)dx} .$
$ = left. {x(2x – cos x)} right|_0^{frac{pi }{2}}$ $ – left. {left( {{x^2} + sin x} right)} right|_0^{frac{pi }{2}}$ $ = frac{{{pi ^2}}}{4} + 1.$
Suy ra $a = 1$, $b = 4$ $ Rightarrow T = {a^2} – 2b = – 7.$
Chọn đáp án C.Ví dụ 14: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = 1 – sin x$, trục hoành và hai đường thẳng $x = 0$, $x = frac{{7pi }}{6}$ bằng $a + frac{{sqrt 3 }}{b} + frac{c}{d}pi $ với $a$, $b$ là các số nguyên, $frac{c}{d}$ là phân số tối giản. Tính $T = a + b + c + d.$
A. $T=16.$
B. $T = 10.$
C. $T = frac{{23}}{2}.$
D. $T = 18.$Lời giải:
Ta có $y = 1 – sin x ge 0$, $forall x in left[ {0;frac{{7pi }}{6}} right].$
Do đó $S = int_0^{frac{{7pi }}{6}} | 1 – sin x|dx$ $ = int_0^{frac{{7pi }}{6}} {(1 – sin x)dx} $ $ = left. {(x + cos x)} right|_0^{frac{{7pi }}{6}}$ $ = frac{{7pi }}{6} – frac{{sqrt 3 }}{2} – 1.$
Suy ra $a = – 1$, $b = – 2$, $c = 7$, $d = 6$ $ Rightarrow T = a + b + c + d = 10.$
Chọn đáp án B.Ví dụ 15: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = {tan ^2}x$, trục hoành, trục tung và đường thẳng $x = frac{pi }{6}$ bằng $frac{{sqrt 3 }}{a} + frac{pi }{b}$ với $a$, $b$ là các số nguyên. Tính $T = {a^2} – b.$
A. $T=3.$
B. $T = 33.$
C. $T = 39.$
D. $T=15.$Lời giải:
Ta có $S = int_0^{frac{pi }{6}} {left| {{{tan }^2}x} right|dx} $ $ = int_0^{frac{pi }{6}} {{{tan }^2}} xdx$ $ = int_0^{frac{pi }{6}} {left( {frac{1}{{{{cos }^2}x}} – 1} right)dx} $ $ = left. {(tan x – x)} right|_0^{frac{pi }{6}}$ $ = frac{{sqrt 3 }}{3} – frac{pi }{6}.$
Suy ra $a = 3$, $b = – 6$ $ Rightarrow T = {a^2} – b = 15.$
Chọn đáp án D.Ví dụ 16: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = xsqrt {1 + {x^2}} $, trục hoành và đường thẳng $x = sqrt 3 $ bằng $frac{a}{b}$ với $frac{a}{b}$ là phân số tối giản. Điểm $M(a;b)$ thuộc miền nghiệm của bất phương trình nào sau đây?
A. $x + y > 9.$
B. $2x + y < 15.$
C. $x + 2y < 13.$
D. $x + 5y > 25.$Lời giải:
Xét phương trình $xsqrt {1 + {x^2}} = 0$ $ Leftrightarrow x = 0.$
Do đó $S = int_0^{sqrt 3 } {|xsqrt {1 + {x^2}} |dx} $ $ = int_0^{sqrt 3 } x sqrt {1 + {x^2}} dx.$
Đặt $t = sqrt {1 + {x^2}} $ $ Rightarrow {t^2} = 1 + {x^2}$ $ Rightarrow xdx = tdt.$
Đổi cận: Suy ra $S = int_1^2 {{t^2}} dt$ $ = left. {frac{{{t^3}}}{3}} right|_1^2 = frac{7}{3}$ $ Rightarrow a = 7$, $b = 3$ $ Rightarrow M(7;3).$
Suy ra $S = int_1^2 {{t^2}} dt$ $ = left. {frac{{{t^3}}}{3}} right|_1^2 = frac{7}{3}$ $ Rightarrow a = 7$, $b = 3$ $ Rightarrow M(7;3).$
Ta có $7 + 3 > 9$ suy ra điểm $M(7;3)$ thuộc miền nghiệm bất phương trình $x + y > 9.$
Chọn đáp án A.Ví dụ 17: Tính diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y = {x^2} – 2x + m$ $(m ge 1)$, trục hoành và các đường thẳng $x = 0$, $x = 2.$
A. $S = 2m + frac{2}{3}.$
B. $S = 2m – frac{2}{3}.$
C. $S = 2m – frac{4}{3}.$
D. $S = 2m + frac{4}{3}.$Lời giải:
Ta có $y = {x^2} – 2x + m$ $ = {(x – 1)^2} + m – 1 ge 0$, $forall m ge 1$, $forall x in [0;2].$
Do đó $S = int_0^2 {left| {{x^2} – 2x + m} right|dx} $ $ = int_0^2 {left( {{x^2} – 2x + m} right)dx} .$
$ = left. {left( {frac{{{x^3}}}{3} – {x^2} + mx} right)} right|_0^2$ $ = 2m – frac{4}{3}.$
Chọn đáp án C.Ví dụ 18: Tính diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y = {x^2} – 9$, trục hoành, trục tung và đường thẳng $x = m$ $(m > 3).$
A. $S = frac{{{m^3}}}{3} – 9m.$
B. $S = frac{{{m^3}}}{3} – 9m + 36.$
C. $S = frac{{{m^3}}}{3} + 9m + 36.$
D. $S = frac{{{m^3}}}{3} – 9m + 18.$Lời giải:
Ta có: $S = int_0^m {left| {{x^2} – 9} right|dx} .$
Bảng xét dấu: Do đó $S = – int_0^3 {left( {{x^2} – 9} right)dx} $ $ + int_3^m {left( {{x^2} – 9} right)dx} .$
Do đó $S = – int_0^3 {left( {{x^2} – 9} right)dx} $ $ + int_3^m {left( {{x^2} – 9} right)dx} .$
$ = – left. {left( {frac{{{x^3}}}{3} – 9x} right)} right|_0^3$ $ + left. {left( {frac{{{x^3}}}{3} – 9x} right)} right|_3^m$ $ = frac{{{m^3}}}{3} – 9m + 36.$
Chọn đáp án B.Ví dụ 19: Cho hình thang cong $(H)$ giới hạn bởi các đường $y = {e^x}$, $y = 0$, $x = 0$, $x = ln 4.$ Đường thẳng $x = k$ $(0 < k < ln 4)$ chia $(H)$ thành hai phần có diện tích là ${S_1}$ và ${S_2}$ như hình vẽ bên.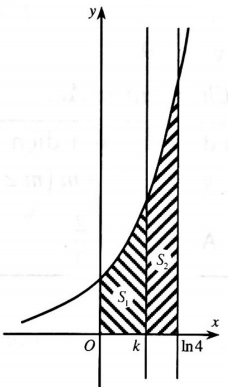 Tìm $k$ để ${{S_1} = 2{S_2}.}$
Tìm $k$ để ${{S_1} = 2{S_2}.}$
A. $k = frac{2}{3}ln 4.$
B. $k = ln 2.$
C. $k = ln frac{8}{3}.$
D. $k = ln 3.$Lời giải:
Từ đồ thị ta có:
${S_1} = int_0^k {{e^x}} dx$ $ = left. {{e^x}} right|_0^k$ $ = {e^k} – 1.$
${S_2} = int_k^{ln 4} {{e^x}} dx$ $ = left. {{e^x}} right|_k^{ln 4}$ $ = 4 – {e^k}.$
Khi đó ${S_1} = 2{S_2}$ $ Rightarrow {e^k} – 1 = 8 – 2{e^k}$ $ Leftrightarrow k = ln 3.$
Chọn đáp án D.Ví dụ 20: Cho hàm số $y = {x^4} – 3{x^2} + m$ có đồ thị $left( {{C_m}} right)$ với $m$ là tham số thực. Giả sử $left( {{C_m}} right)$ cắt trục $Ox$ tại bốn điểm phân biệt như hình vẽ bên. Gọi ${S_1}$, ${S_2}$ và ${S_3}$ là diện tích các miền gạch chéo được cho trên hình vẽ.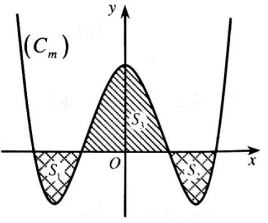 Tìm $m$ để ${{S_1} + {S_2} = {S_3}.}$
Tìm $m$ để ${{S_1} + {S_2} = {S_3}.}$
A. $m = – frac{5}{2}.$
B. $m = – frac{5}{4}.$
C. $m = frac{5}{2}.$
D. $m = frac{5}{4}.$Lời giải:
Gọi $x = a$, $x = b$ $(a < b)$ lần lượt là các nghiệm dương của phương trình x^{4}-3 x^{2}+m=0
Do đó ${b^4} – 3{b^2} + m = 0$ $(1).$
Ta có ${S_1} + {S_2} = {S_3}$, kết hợp đồ thị $ Rightarrow frac{1}{2}{S_3} = {S_2}.$
$int_0^a {left( {{x^4} – 3{x^2} + m} right)dx} $ $ = – int_a^b {left( {{x^4} – 3{x^2} + m} right)dx} .$
$ Leftrightarrow int_0^b {left( {{x^4} – 3{x^2} + m} right)dx} = 0.$
$left. { Leftrightarrow left( {frac{{{x^5}}}{5} – {x^3} + mx} right)} right|_0^b = 0.$
$ Leftrightarrow frac{{{b^5}}}{5} – {b^3} + mb = 0$ $ Rightarrow frac{{{b^4}}}{5} – {b^2} + m = 0$ $(2)$ (vì $b>0$).
Từ $(1)$ và $(2)$, trừ vế theo vế ta được $frac{4}{5}{b^4} – 2{b^2} = 0$ $ Rightarrow {b^2} = frac{5}{2}$ (vì $b > 0$).
Thay ${b^2} = frac{5}{2}$ vào $(1)$ ta được $m = frac{5}{4}.$
Chọn đáp án D.III. LUYỆN TẬP
1. ĐỀ BÀI
Câu 1: Cho hàm số $y = f(x)$ liên tục trên đoạn $[a;b].$ Diện tích hình phẳng giới hạn bởi đường cong $y = f(x)$, trục hoành, các đường thẳng $x = a$, $x = b$ là:
A. $int_b^a f (x)dx.$
B. $int_a^b | f(x)|dx.$
C. $int_a^b f (x)dx.$
D. $pi int_a^b {{f^2}} (x)dx.$Câu 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = 4x – {x^3}$, trục hoành, trục tung và đường thẳng $x=4$ bằng:
A. $48.$
B. $44.$
C. $40.$
D. $36.$Câu 3: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = frac{{ – 3x – 1}}{{x – 1}}$ và hai trục tọa độ bằng $4ln frac{a}{b} + c$ với $a$, $b$ là các số nguyên dương, $frac{a}{b}$ là phân số tối giản, $c$ là số nguyên. Tính $T = a + b + c.$
A. $T=5.$
B. $T=6.$
C. $T=7.$
D. $T=8.$Câu 4: Cho diện tích hình phẳng giới hạn bởi đường cong $y = frac{{ln x}}{{{x^2}}}$, trục $Ox$ và hai đường thẳng $x = 1$, $x = e$ bằng $a + frac{b}{e}$ với $a$, $b$ là các số nguyên. Tính $T = {log _2}(14a – b).$
A. $T=1.$
B. $T=2.$
C. $T=3.$
D. $T=4.$ Câu 5: Cho diện tích hình phẳng giới hạn bởi các đường $y = 1 – {x^2}$, $y = 0$ bằng $frac{a}{b}$ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $T= 2a+b.$
A. $T=10.$
B. $T=11.$
C. $T=13.$
D. $T=15.$ Câu 6: Hình phẳng giới hạn bởi các đường $y = 3{x^3} + 2x$, $y = 0$, $x = a$ $(a > 0)$ có diện tích bằng $frac{7}{4}$ thì giá trị của $a$ bằng:
A. $1.$
B. $frac{{sqrt 7 }}{2}.$
C. $2.$
D. $3.$ Câu 7: Cho diện tích hình phẳng giới hạn bởi các đường $y = x{e^x}$, $y = 0$, $x = – 1$, $x = 2$ bằng ${e^2} + frac{a}{e} + b$ với $a$, $b$ là các số nguyên. Tính $T = a + 2b.$
A. $T=-4.$
B. $T=-2.$
C. $T=2.$
D. $T=4.$ Câu 8: Hình phẳng giới hạn bởi các đường $y = 0$, $y = {x^2} – 2x$, $x = – 1$, $x = 2$ có diện tích được tính theo công thức:
A. $S = int_{ – 1}^0 {left( {{x^2} – 2x} right)dx} $ $ – int_0^2 {left( {{x^2} – 2x} right)dx} .$
B. $S = – int_{ – 1}^0 {left( {{x^2} – 2x} right)dx} $ $ + int_0^2 {left( {{x^2} – 2x} right)dx} .$
C. $S = int_{ – 1}^2 {left( {{x^2} – 2x} right)dx} .$
D. $S = int_{ – 1}^0 {left( {{x^2} – 2x} right)dx} $ $ + int_0^2 {left( {{x^2} – 2x} right)dx.} $Câu 9: Cho diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = {x^4} + 3{x^2} + 1$, trục hoành và hai đường thẳng $x = 0$, $x = 1$ bằng $frac{a}{b}$ với $a$, $b$ là các số nguyên và $frac{a}{b}$ là phân số tối giản. Tính $T = 2a – b.$
A. $T = 17.$
B. $T=-1.$
C. $T=-17.$
D. $T=1.$ Câu 10: Hình vuông $OABC$ có cạnh bằng $4$ được chia thành hai phần bởi đường cong $(C)$ có phương trình $y = frac{1}{4}{x^2}.$ Gọi ${S_1}$, ${S_2}$ là diện tích của phần không bị gạch và phần bị gạch (như hình vẽ).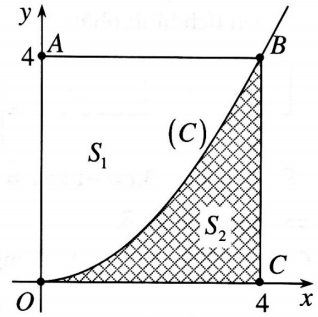 Tính tỉ số $frac{{{S_1}}}{{{S_2}}}.$
Tính tỉ số $frac{{{S_1}}}{{{S_2}}}.$
A. $frac{{{S_1}}}{{{S_2}}} = frac{3}{2}.$
B. $frac{{{S_1}}}{{{S_2}}} = frac{1}{2}.$
C. $frac{{{S_1}}}{{{S_2}}} = 2.$
D. $frac{{{S_1}}}{{{S_2}}} = 1.$2. BẢNG ĐÁP ÁN3. HƯỚNG DẪN GIẢI
Câu 1: Áp dụng công thức tính diện tích hình phẳng giới hạn bởi các đường cong $y = f(x)$, trục hoành, các đường thẳng $x=a$, $x = b$ là: $S = int_a^b | f(x)|dx.$
Chọn đáp án B.Câu 2: Diện tích hình phẳng:
$S = int_0^4 {left| {4x – {x^3}} right|dx} $ $ = left| {int_0^2 {left( {4x – {x^3}} right)dx} } right|$ $ + left| {int_2^4 {left( {4x – {x^3}} right)dx} } right|$ $ = 40.$
Chọn đáp án C.Câu 3: Phương trình hoành độ giao điểm: $frac{{ – 3x – 1}}{{x – 1}} = 0$ $ Leftrightarrow x = frac{{ – 1}}{3}.$
Diện tích hình phẳng $S = left| {int_{ – frac{1}{3}}^0 {frac{{ – 3x – 1}}{{x – 1}}dx} } right|$ $ = left| {int_{ – frac{1}{3}}^0 {left( { – 3 – frac{4}{{x – 1}}} right)dx} } right|.$
$ = left| {left. {( – 3x – 4ln |x – 1|)} right|_{ – frac{1}{3}}^0} right|$ $ = left| { – 1 + 4ln frac{4}{3}} right|$ $ = 4ln frac{4}{3} – 1.$
Suy ra $a = 4$, $b = 3$, $c = – 1$ $ Rightarrow T = a + b + c = 6.$
Chọn đáp án B.Câu 4: Diện tích hình phẳng:
$S = int_1^e {left| {frac{{ln x}}{{{x^2}}}} right|dx} $ $ = int_1^e {frac{{ln x}}{{{x^2}}}dx} .$
Đặt $left{ {begin{array}{*{20}{l}}
{u = ln x}\
{dv = frac{{dx}}{{{x^2}}}}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{{dx}}{x}}\
{v = – frac{1}{x}}
end{array}} right..$
$S = – left. {frac{{ln x}}{x}} right|_1^e$ $ + int_1^e {frac{{dx}}{{{x^2}}}} $ $ = – frac{1}{e} – left. {frac{1}{x}} right|_1^e$ $ = 1 – frac{2}{e}$ $ Rightarrow a = 1$, $b = – 2$ $ Rightarrow T = {log _2}(14a – b) = 4.$
Chọn đáp án D.Câu 5: Phương trình hoành độ giao điểm: $1 – {x^2} = 0$ $ Leftrightarrow x = pm 1.$
Diện tích $S = int_{ – 1}^1 {left| {1 – {x^2}} right|dx} = frac{4}{3}$ $ Rightarrow a = 4$, $b = 3$ $ Rightarrow T = 2a + b = 11.$
Chọn đáp án B.Câu 6: Phương trình hoành độ giao điểm: $3{x^3} + 2x = 0$ $ Leftrightarrow x = 0.$
Diện tích hình phẳng là $S = left| {int_0^a {left( {3{x^3} + 2x} right)dx} } right|$ $ = left| {left. {left( {frac{{3{x^4}}}{4} + {x^2}} right)} right|_0^a} right|$ $ = frac{{3{a^4}}}{4} + {a^2}.$
$S = frac{7}{4}$ $ Rightarrow frac{{3{a^4}}}{4} + {a^2} = frac{7}{4}$ $ Leftrightarrow {a^2} = 1$ $ Rightarrow a = 1.$
Chọn đáp án A.Câu 7: Diện tích $S = int_{ – 1}^2 {left| {x{e^x}} right|dx} $ $ = – int_{ – 1}^0 x {e^x}dx + int_0^2 x {e^x}dx.$
Sử dụng bảng: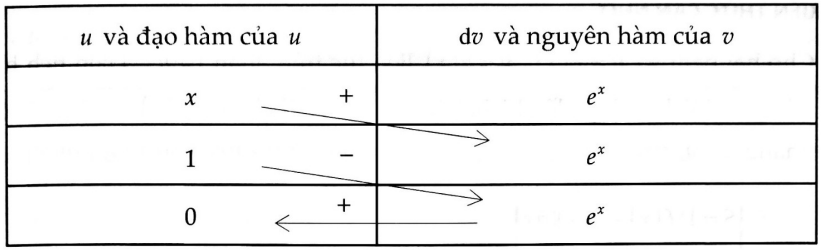 Suy ra $S = – left. {left( {x{e^x} – {e^x}} right)} right|_{ – 1}^0$ $ + left. {left( {x{e^x} – {e^x}} right)} right|_0^2$ $ = {e^2} – frac{2}{e} + 2$ $ Rightarrow a = – 2$, $b = 2$ $ Rightarrow T = a + 2b = 2.$
Suy ra $S = – left. {left( {x{e^x} – {e^x}} right)} right|_{ – 1}^0$ $ + left. {left( {x{e^x} – {e^x}} right)} right|_0^2$ $ = {e^2} – frac{2}{e} + 2$ $ Rightarrow a = – 2$, $b = 2$ $ Rightarrow T = a + 2b = 2.$
Chọn đáp án C.Câu 8: $S = int_{ – 1}^2 {left| {{x^2} – 2x} right|dx} $ $ = int_{ – 1}^0 {left| {{x^2} – 2x} right|dx} + int_0^2 {left| {{x^2} – 2x} right|dx} .$
$ = int_{ – 1}^0 {left( {{x^2} – 2x} right)dx} – int_0^2 {left( {{x^2} – 2x} right)dx} .$
Chọn đáp án A.Câu 9: $S = int_0^1 {left| {{x^4} + 3{x^2} + 1} right|dx} = frac{{11}}{5}$ $ Rightarrow a = 11$, $b = 5$$ Rightarrow S = 2a – b = 17.$
Chọn đáp án A.Câu 10: Ta có:
${S_2} = int_0^4 {left( {frac{1}{4}{x^2}} right)dx} $ $ = left. {frac{{{x^3}}}{{12}}} right|_0^4 = frac{{16}}{3}.$
${S_1} = {S_{OABC}} – {S_2}$ $ = 16 – frac{{16}}{3} = frac{{32}}{3}$ $ Rightarrow frac{{{S_1}}}{{{S_2}}} = 2.$
Chọn đáp án C.

Be the first to comment