Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Giải tích 12 nâng cao: Ứng dụng tích phân để tính diện tích hình phẳng.CÂU HỎI VÀ BÀI TẬPBài 26. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = sin x + 1$, trục hoành và hai đường thẳng $x = 0$ và $x = frac{{7pi }}{6}.$Lời giải:
Ta thấy $sin x + 1 ge 0$, $forall x in left( {0;frac{{7pi }}{6}} right)$ nên diện tích $S$ cần tìm bằng:
$S = int_0^{frac{{7pi }}{6}} | sin x + 1|dx$ $ = int_0^{frac{{7pi }}{6}} {(sin x + 1)dx} $ $ = left. {( – cos x + x)} right|_0^{frac{{7pi }}{6}}.$
$ = left( { – cos frac{{7pi }}{6} + frac{{7pi }}{6}} right)$ $ – ( – cos 0 + 0)$ $ = frac{{sqrt 3 }}{2} + frac{{7pi }}{6} + 1.$Bài 27. Tính diện tích hình phẳng giới hạn bởi:
a) Đồ thị hàm số $y = {cos ^2}x$, trục hoành, trục tung và đường thẳng $x = pi .$
b) Đồ thị hai hàm số $y = sqrt x $ và $y = sqrt[3]{x}.$
c) Đồ thị hai hàm số $y = 2{x^2}$ và $y = {x^4} – 2{x^2}$ trong miền $x > 0.$Lời giải:
a) Diện tích $S$ cần tìm:
$S = int_0^pi {{{cos }^2}} xdx$ $ = int_0^pi {frac{{1 + cos 2x}}{2}dx} $ $ = left. {frac{1}{2}x} right|_0^pi + left. {frac{{sin 2x}}{4}} right|_0^pi $ $ = frac{pi }{2}.$
b) Hoành độ giao điểm của đồ thị hai hàm số $y = sqrt x $ và $y = sqrt[3]{x}$ là nghiệm của phương trình:
$sqrt x = sqrt[3]{x}$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{{x^3} = {x^2}}\
{x ge 0}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{x = 0}\
{x = 1}
end{array}} right..$
Diện tích cần tìm $S = int_0^1 | sqrt x – sqrt[3]{x}|dx$ $ = int_0^1 {(sqrt[3]{x} – sqrt x )dx} .$
$ = int_0^1 {left( {{x^{frac{1}{3}}} – {x^{frac{1}{2}}}} right)dx} $ $ = left. {left( {frac{{{x^{frac{4}{3}}}}}{{frac{4}{3}}} – frac{{{x^{frac{3}{2}}}}}{{frac{3}{2}}}} right)} right|_0^1$ $ = frac{3}{4} – frac{2}{3} = frac{1}{{12}}.$
c) Phương trình hoành độ giao điểm đồ thị hai hàm số: $y = 2{x^2}$ và $y = {x^4} – 2{x^2}$ (với $x > 0$).
$2{x^2} = {x^4} – 2{x^2}$ $ Leftrightarrow {x^4} – 4{x^2} = 0$ $ Leftrightarrow {x^2}left( {{x^2} – 4} right) = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 0}\
{x = 2}
end{array}} right..$
Vậy diện tích cần tìm $S = int_0^2 {left| {{x^4} – 2{x^2} – 2{x^2}} right|dx} $ $ = int_0^2 {left| {{x^4} – 4{x^2}} right|dx} .$
$ = int_0^2 {{x^2}} left| {{x^2} – 4} right|dx$ $ = int_0^2 {{x^2}} left( {4 – {x^2}} right)dx$ $ = int_0^2 {left( {4{x^2} – {x^4}} right)dx} .$
$ = left. {left( {frac{{4{x^3}}}{3} – frac{{{x^5}}}{5}} right)} right|_0^2$ $ = frac{{32}}{3} – frac{{32}}{5} = frac{{64}}{{15}}.$Bài 28. Tính diện tích các hình phẳng giới hạn bởi:
a) Đồ thị các hàm số $y = {x^2} – 4$, $y = – {x^2} – 2x$ và hai đường thẳng $x = – 3$, $x = – 2.$
b) Đồ thị hai hàm số $y = {x^2} – 4$ và $y = – {x^2} – 2x.$
c) Đồ thị hàm số $y = {x^3} – 4x$, trục hoành, đường thẳng $x = -2$ và đường thẳng $x = 4.$Lời giải: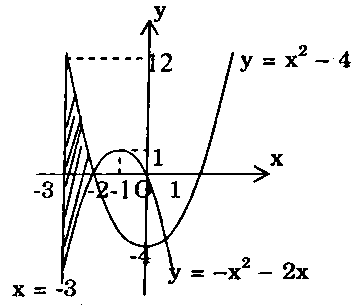
a) Dựa vào hình vẽ ta thấy diện tích hình phẳng cần tìm là:
$S = int_{ – 3}^2 {left| {left( {{x^2} – 4} right) – left( { – {x^2} – 2x} right)} right|dx} .$
$ = int_{ – 3}^{ – 2} {left[ {left( {{x^2} – 4} right) – left( { – {x^2} – 2x} right)} right]dx.} $
$ = int_{ – 3}^2 {left( {2{x^2} + 2x – 4} right)dx} .$
$ = left. {left( {2frac{{{x^3}}}{3} + 2frac{{{x^2}}}{2} – 4x} right)} right|_{ – 3}^{ – 2}$ $ = frac{{11}}{3}.$
Chú ý: Ở câu này, nếu không vẽ hình thì phải chứng tỏ được rằng $forall x in [ – 3; – 2]$ thì $left( {{x^2} – 4} right) – left( { – {x^2} – 2x} right) ge 0$ để phá được dấu giá trị tuyệt đối.
b) Phương trình hoành độ giao điểm đồ thị hai hàm số đã cho là:
${x^2} – 4 = – {x^2} – 2x$ $ Leftrightarrow {x^2} + x – 2 = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 1}\
{x = – 2}
end{array}} right..$
Dựa vào hình vẽ ở câu a ta có:
$S = int_{ – 2}^1 {left| {left( {{x^2} – 4} right) – ( – {x^2} – 2x)} right|dx} $ $ = int_{ – 2}^1 {left[ { – left( {2{x^2} + 2x – 4} right)} right]dx} .$
$ = left. {left( { – 2frac{{{x^3}}}{3} – 2frac{{{x^2}}}{2} + 4x} right)} right|_{ – 2}^1 = 9.$
c) Diện tích cần tìm $S = int_{ – 2}^4 {left| {{x^3} – 4x} right|dx} .$
Ta có: ${x^3} – 4x = xleft( {{x^2} – 4} right) = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 0}\
{x = pm 2}
end{array}} right..$
Bảng xét dấu:
Vậy $S = int_{ – 2}^0 {left( {x_ – ^3 – 4x} right)dx} $ $ + int_0^2 {left[ { – left( {{x^3} – 4x} right)} right]dx} $ $ + int_2^4 {left( {{x^3} – 4x} right)dx} .$
$ = left. {left( {frac{{{x^4}}}{4} – 4frac{{{x^2}}}{2}} right)} right|_{ – 2}^0$ $ + left. {left( {frac{{ – {x^4}}}{4} + frac{{4{x^2}}}{2}} right)} right|_0^2$ $ + left. {left( {frac{{{x^4}}}{4} – 4frac{{{x^2}}}{2}} right)} right|_2^4 = 44.$
Để lại một phản hồi