Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Giải tích 12 nâng cao: Ứng dụng tích phân để tính thể tích vật thể.CÂU HỎI VÀ BÀI TẬPBài 29. Tính thể tích của vật thể nằm giữa hai mặt phẳng $x = -1$ và $x = 1$, biết rằng thiết diện vuông góc với trục $Ox$ tại điểm có hoành độ $x$ $( – 1 le x le 1)$ là một hình vuông cạnh là $2sqrt {1 – {x^2}} .$Lời giải:
Diện tích của thiết diện là $S(x) = {(2sqrt {1 – x} )^2}.$
Thể tích của vật thể cần tìm là: $V = int_{ – 1}^1 {{{(2sqrt {1 – x} )}^2}} dx$ $ = int_{ – 1}^1 {{{(4 – 4x)}^2}} dx.$
$V = int_{ – 1}^1 {{{(2sqrt {1 – x} )}^2}} dx$ $ = int_{ – 1}^1 4 (1 – x)dx$ $ = left. {left( {4x – 2{x^2}} right)} right|_{ – 1}^1 = 8.$Bài 30. Tính thể tích của vật thể nằm giữa hai mặt phẳng $x = 0$ và $x = pi $, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $0 le x le pi $ là một tam giác đều cạnh là $2sqrt {sin x} .$Lời giải:
Diện tích của thiết diện là: $S(x) = frac{1}{2}{(2sqrt {sin x} )^2}.frac{{sqrt 3 }}{2}$ $ = sqrt 3 sin x.$
Vậy thể tích của vật thể đã cho là: $V = int_0^pi {sqrt 3 } sin xdx$ $ = – left. {sqrt 3 cos x} right|_0^pi = 2sqrt 3 .$Bài 31. Cho hình phẳng $A$ giới hạn bởi các đường $y = 0$, $x = 4$ và $y = sqrt x – 1.$ Tính thể tích của khối tròn xoay tạo thành khi quay hình $A$ quanh trục hoành.Lời giải: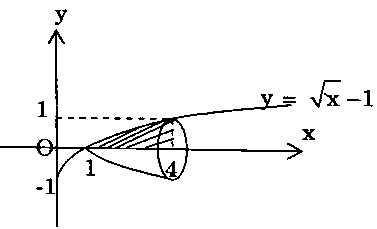
Giao điểm của đường $y = sqrt x – 1$ và đường $y = 0$ có hoành độ là $x = 1$, như vậy: $V = pi int_1^4 {{{(sqrt x – 1)}^2}} dx.$
$ = pi int_1^4 {(x – 2sqrt x + 1)dx} .$
$ = pi left[ {left. {left( {frac{{{x^2}}}{2} – 2.frac{{{x^{frac{3}{2}}}}}{{frac{3}{2}}} + x} right)} right|_1^4} right] = frac{{7pi }}{6}.$Bài 32. Cho hình phẳng $B$ giới hạn bởi các đường $x = frac{2}{y}$, $y = 1$ và $y = 4.$ Tính thể tích của khối tròn xoay tạo thành khi quay hình $B$ quanh trục tung.Lời giải: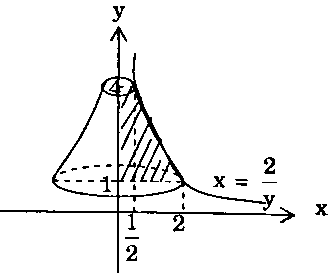
Thể tích vật thể cần tìm là:
$V = pi int_1^4 {{{left( {frac{2}{y}} right)}^2}} dy$ $ = pi int_1^4 {frac{4}{{{y^2}}}dy} $ $ = left. {4pi left( {frac{{ – 1}}{y}} right)} right|_1^4 = 3pi .$Bài 33. Cho hình phẳng $B$ giới hạn bởi các đường $x = sqrt 5 {y^2}$, $x = 0$, $y = – 1$ và $y = 1.$ Tính thể tích của khối tròn xoay tạo thành khi quay hình $B$ quanh trục tung.Lời giải:
Thể tích khối tròn xoay tạo thành:
$V = pi int_{ – 1}^1 {{{left( {sqrt 5 {y^2}} right)}^2}} dy$ $ = pi int_{ – 1}^1 5 {y^4}dy$ $ = left. {5pi frac{{{y^5}}}{5}} right|_{ – 1}^1 = 2pi .$LUYỆN TẬPBài 34. Tính diện tích hình phẳng giới hạn bởi:
a) Đồ thị các hàm số $y = x$, $y = 1$ và $y = frac{{{x^2}}}{4}$ trong miền $x ge 0$, $y le 1.$
b) Đồ thị hai hàm số $y = {x^4} – 4{x^2} + 4$, $y = {x^2}$, trục tung và đường thẳng $x = 1.$
c) Đồ thị các hàm số $y = {x^2}$, $y = 4x – 4$ và $y = – 4x – 4.$Lời giải:
a) Cách 1: Hoành độ giao điểm của đường thẳng $y = x$ và $y = 1$ là $x = 1.$
Hoành độ giao điểm của đường thẳng $y = 1$ và đường cong $y = frac{{{x^2}}}{4}$ trong miền $x ge 0$ là $x = 2.$
Diện tích hình phẳng cần tìm chính là tổng diện tích tam giác cong $OAC$ và tam giác cong $ACB.$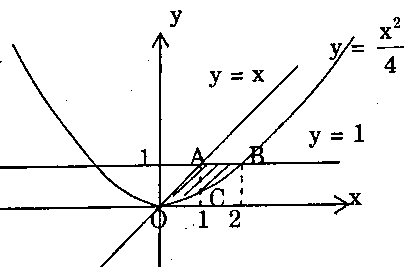
Diện tích tam giác cong $OAC$ là:
$int_0^1 {left( {x – frac{{{x^2}}}{4}} right)dx} $ $ = left. {left( {frac{{{x^2}}}{2} – frac{{{x^3}}}{{12}}} right)} right|_0^1 = frac{5}{{12}}.$
Diện tích tam giác cong $ACB$ là:
$int_1^2 {left( {1 – frac{{{x^2}}}{4}} right)dx} $ $ = left. {left( {x – frac{{{x^3}}}{{12}}} right)} right|_1^2 = frac{5}{{12}}.$
Vậy diện tích hình phẳng cần tìm là: $frac{5}{{12}} + frac{5}{{12}} = frac{5}{6}.$
Cách 2: Coi hình phẳng đã cho là hình phẳng giới hạn bởi đường cong có phương trình $x = 2sqrt y $, đường thẳng $x = y$, $y = 0$ và đường thẳng $y = 1.$ Diện tích cần tìm là:
$S = int_0^1 {(2sqrt y – y)dy} $ $ = left. {left( {2frac{{ysqrt y }}{{frac{3}{2}}} – frac{{{y^2}}}{2}} right)} right|_0^1 = frac{5}{6}.$
b) Diện tích hình phẳng cần tìm là:
$S = int_0^1 {left| {{x^4} – 4{x^2} + 4 – {x^2}} right|dx} $ $ = int_0^1 {left| {{x^4} – 5{x^2} + 4} right|dx} .$
Vì ${x^4} – 5{x^2} + 4$ $ = left( {{x^2} – 1} right)left( {{x^2} – 4} right) ge 0$, $forall x in [0;1].$
Nên $S = int_0^1 {left( {{x^4} – 5{x^2} + 4} right)dx} $ $ = left. {left( {frac{{{x^5}}}{5} – frac{{5{x^3}}}{3} + 4x} right)} right|_0^1$ $ = frac{1}{5} – frac{5}{3} + 4 = frac{{38}}{{15}}.$
c) Ta thấy đường thẳng $y = -4x – 4$ và đường thẳng $y = 4x – 4$ lần lượt là hai tiếp tuyến của đồ thị hàm số $y = {x^2}$ tại các tiếp điểm có hoành độ $x = -2$ và $x = 2.$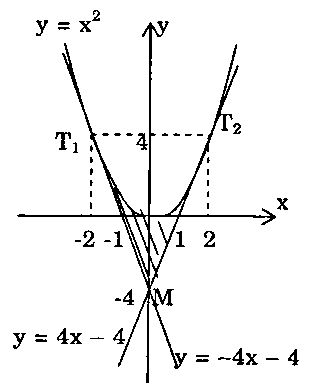
Do tính đối xứng qua $Oy$ của parabol $y = {x^2}$ nên diện tích hình phẳng cần tìm bằng $2$ lần diện tích tam giác cạnh $OM{T_2}$ và bằng:
$S = 2int_0^2 {left[ {{x^2} – (4x – 4)} right]dx} $ $ = 2int_0^2 {{{(x – 2)}^2}} dx.$
$ = left. {2.frac{{{{(x – 2)}^3}}}{3}} right|_0^2 = frac{{16}}{3}.$Bài 35. Tính diện tích hình phẳng giới hạn bởi:
a) Đồ thị hai hàm số $y = {x^2} + 1$ và $y = 3 – x.$
b) Các đường có phương trình $x = {y^3}$, $y = 1$ và $x = 8.$
c) Đồ thị hai hàm số $y = sqrt x $, $y = 6 – x$ và trục hoành.Lời giải:
a) Hoành độ giao điểm đồ thị hai hàm số $y = {x^2} + 1$ và $y = 3 – x$ là nghiệm của phương trình: ${x^2} + 1 = 3 – x$ $ Leftrightarrow {x^2} + x – 2 = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{x = 1}\
{x = – 2}
end{array}} right..$
Vậy diện tích cần tìm là: $S = int_{ – 2}^1 {left| {left( {{x^2} + 1} right) – (3 – x)} right|dx} $ $ = int_{ – 2}^1 {left| {{x^2} + x – 2} right|dx} .$
$ = – int_{ – 2}^1 {left( {{x^2} + x – 2} right)dx} $ $ = – left. {left( {frac{{{x^3}}}{3} + frac{{{x^2}}}{2} – 2x} right)} right|_{ – 2}^1 = frac{9}{2}.$
b) Tung độ giao điểm của đường cong $x = {y^3}$ và đường thẳng $x = 8$ là nghiệm của phương trình ${y^3} = 8$ $ Leftrightarrow y = 2.$ Vậy diện tích cần tìm là:
$S = int_1^2 {left| {{y^3} – 8} right|dy} $ $ = – int_1^2 {left( {{y^3} – 8} right)dy} $ $ = – left. {left( {frac{{{y^4}}}{4} – 8y} right)} right|_1^2.$
$ = – left[ {left( {frac{{16}}{4} – 16} right) – left( {frac{1}{4} – 8} right)} right] = frac{{17}}{4}.$
c) Ta có: $y = sqrt x $ $ Leftrightarrow x = {y^2}$ $(y ge 0)$, $y = 6 – x$ $ Leftrightarrow x = 6 – y.$
Tung độ giao điểm của hai đường $x = {y^2}$, $x = 6 – y$ là nghiệm của phương trình ${y^2} = 6 – y$ $ Leftrightarrow {y^2} + y – 6 = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}}
{y = – 3,,({rm{loại}},{rm{vì}},y ge 0)}\
{y = 2}
end{array}} right..$
Vậy diện tích cần tìm là: $S = int_0^2 {left| {{y^2} – (6 – y)} right|dy} $ $ = int_0^2 {left| {{y^2} + y – 6} right|dy} .$
$ = – int_0^2 {left( {{y^2} + y – 6} right)dy} $ $ = – left. {left( {frac{{{y^3}}}{3} + frac{{{y^2}}}{2} – 6y} right)} right|_0^2$ $ = – left( {frac{8}{3} + frac{4}{2} – 12} right) = frac{{22}}{3}.$Bài 36. Tính thể tích của vật thể $T$ nằm giữa hai mặt phẳng $x = 0$ và $x = pi $, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục $Ox$ tại điểm có hoành độ $x$ $(0 le x le pi )$ là một hình vuông cạnh là $2sqrt {sin x} .$Lời giải:
Diện tích thiết diện là $S(x) = {(2sqrt {sin x} )^2}.$
Vậy thể tích của vật $T$ được tính bởi:
$V = int_0^pi {{{(2sqrt {sin x} )}^2}} dx$ $ = int_0^pi 4 sin xdx$ $ = – left. {4cos x} right|_0^pi $ $ = – 4( – 1 – 1) = 8.$Bài 37. Cho hình phẳng $A$ giới hạn bởi các đường $y = {x^2}$, $y = 0$, $x = 0$ và $x = 2.$ Tính thể tích của khối tròn xoay tạo thành khi quay hình $A$ quanh trục hoành.Lời giải: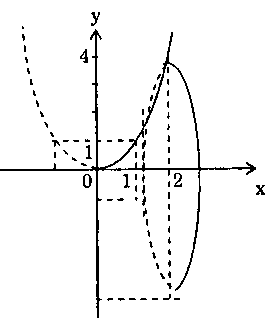
Thể tích khối tròn xoay tạo thành được tính theo công thức:
$V = pi int_0^2 {{x^4}} dx$ $ = left. {pi .frac{{{x^5}}}{5}} right|_0^2 = frac{{32pi }}{5}.$
Vậy thể tích cần tìm là: $V = frac{{32pi }}{5}.$Bài 38. Cho hình phẳng $A$ giới hạn bởi các đường $y = cos x$, $y = 0$, $x = 0$ và $x = frac{pi }{4}.$ Tính thể tích khối tròn xoay tạo thành khi quay hình $A$ quanh trục hoành.Lời giải:
Thể tích cần tìm là: $V = pi int_0^{frac{pi }{4}} {{{(cos x)}^2}} dx$ $ = pi int_0^{frac{pi }{4}} {frac{{1 + cos 2x}}{2}dx} .$
$ = left. {frac{pi }{2}left( {x + frac{1}{2}sin 2x} right)} right|_0^{frac{pi }{4}}$ $ = frac{pi }{2}left( {frac{pi }{4} + frac{1}{2}} right)$ $ = frac{{{pi ^2}}}{8} + frac{pi }{4}.$Bài 39. Cho hình phẳng $A$ giới hạn bởi các đường $y = x.{e^{frac{x}{2}}}$, $y = 0$, $x = 0$ và $x = 1.$ Tính thể tích của khối tròn xoay tạo thành khi quay hình $A$ quanh trục hoành.Lời giải:
Ta có: $V = pi int_0^1 {{{left( {x.{e^{frac{x}{2}}}} right)}^2}} dx$ $ = pi int_0^1 {{x^2}} .{e^x}dx.$
Tính tích phân $I = int_0^1 {{x^2}} .{e^x}dx$ ta có:
Đặt $left{ {begin{array}{*{20}{l}}
{u(x) = {x^2}}\
{v'(x) = {e^x}}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{u'(x) = 2x}\
{v(x) = {e^x}}
end{array}} right.$ $ Rightarrow I = left. {{x^2}.{e^x}} right|_0^1 – int_0^1 2 x.{e^x}dx$ $ = e – 2int_0^1 x .{e^x}dx.$
Tính ${I_1} = int_0^1 x .{e^x}dx$ ta có:
Đặt $left{ {begin{array}{*{20}{l}}
{{u_1}(x) = x}\
{{v_1}'(x) = {e^x}}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{{u_1}'(x) = 1}\
{{v_1}(x) = {e^x}}
end{array}} right..$
$ Rightarrow {I_1} = x.left. {{e^x}} right|_0^1 – int_0^1 {{e^x}} dx$ $ = e – left. {{e^x}} right|_0^1$ $ = e – (e – 1) = 1.$
$ Rightarrow I = e – 2.1 = e – 2.$
Vậy $V = pi (e – 2).$Bài 40. Cho hình phẳng $B$ giới hạn bởi các đường $x = sqrt {2sin 2y} $, $x = 0$, $y = 0$ và $y = frac{pi }{2}.$ Tính thể tích của khối tròn xoay tạo thành khi quay hình $B$ quanh trục tung.Lời giải:
Thể tích vật thể tròn xoay cần tìm là:
$V = pi int_0^{frac{pi }{2}} {{{(sqrt {2sin 2y} )}^2}} dy$ $ = pi int_0^{frac{pi }{2}} 2 sin 2ydy$ $ = – left. {pi cos 2y} right|_0^{frac{pi }{2}}.$
$ = – pi (cos pi – cos 0)$ $ = – pi ( – 1 – 1) = 2pi .$
Để lại một phản hồi