Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Giải tích 12 nâng cao: Tích phân.CÂU HỎI VÀ BÀI TẬPBài 10. Không tìm nguyên hàm, hãy tính các tích phân sau:
a) $int_{ – 2}^4 {left( {frac{x}{2} + 3} right)dx.} $
b) $int_{ – 1}^2 {|x|dx} .$
c) $int_{ – 3}^3 {sqrt {9 – {x^2}} } dx.$Lời giải:
a) Vẽ đồ thị $y = frac{x}{2} + 3.$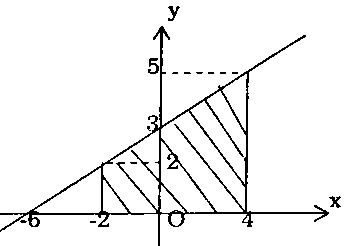
Suy ra diện tích $S$ của hình phẳng giới hạn bởi $y = frac{x}{2} + 3$ và $x = – 2$, $x = 4$, trục hoành là diện tích hình thang có chiều cao bằng $6$ và hai đáy bằng $2$ và bằng $5$, cho nên:
$S = frac{1}{2}(2 + 5) times 6 = 21$ (đvdt).
Vậy $int_{ – 2}^4 {left( {frac{x}{2} + 3} right)dx} = 21.$
b) Vẽ đồ thị $y = |x|.$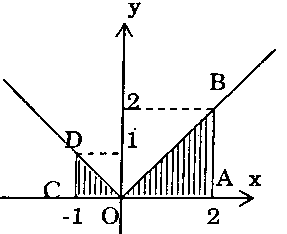
Diện tích hình phẳng giới hạn bởi $y = |x|$, trục hoành, $x = -1$, $x = 2$ bằng tổng diện tích tam giác vuông $OAB$ và diện tích $Delta OCD.$
${S_{Delta OAB}} = frac{1}{2}OA.AB$ $ = frac{1}{2}.2.2 = 2$, ${S_{Delta OCD}} = frac{1}{2}.$
Vậy $int_{ – 1}^2 {|x|dx} = 2 + frac{1}{2} = frac{5}{2}.$
c) Vẽ đồ thị $y = sqrt {9 – {x^2}} $ là nửa đường tròn, bán kính $R = 3$, diện tích nửa đường tròn là: $S = frac{1}{2}pi {R^2}$ $ = frac{1}{2}pi {.3^2} = frac{{9pi }}{2}.$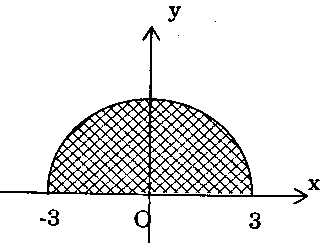
Vậy $int_{ – 3}^3 {sqrt {9 – {x^2}} } dx = frac{{9pi }}{2}.$Bài 11. Cho biết $int_1^2 f (x)dx = – 4$, $int_1^5 f (x)dx = 6$, $int_1^5 g (x)dx = 8.$ Hãy tính:
a) $int_2^5 f (x)dx.$
b) $int_1^2 3 f(x)dx.$
c) $int_1^5 {[f(x) – g(x)]dx} .$
d) $int_1^5 {[4f(x) – g(x)]dx} .$Lời giải:
a) Ta có: $int_1^5 f (x)dx$ $ = int_1^2 f (x)dx + int_2^5 f (x)dx.$
$ Leftrightarrow 6 = – 4 + int_2^5 f (x)dx$ $ Leftrightarrow int_2^5 f (x)dx = 10.$
Vậy $int_2^5 f (x)dx = 10.$
b) $int_1^2 3 f(x)dx$ $ = 3int_1^2 f (x)dx = – 12.$
c) $int_1^5 {[f(x) – g(x)]dx} $ $ = int_1^5 f (x)dx – int_1^5 g (x)dx$ $ = 6 – 8 = – 2.$
d) $int_1^5 {[4{rm{ }}f(x) – g(x)]dx} $ $ = 4int_1^5 f (x)dx – int_1^5 g (x)dx$ $ = 4.6 – 8 = 16.$Bài 12. Cho $int_0^3 f (z)dz = 3$, $int_0^4 f (x)dx = 7.$ Hãy tính $int_3^4 f (t)dt.$Lời giải:
Ta có $int_0^3 f (z)dz = 3$, $int_0^4 f (x)dx = 7$ $ Rightarrow int_0^3 f (t)dt = 3$ và $int_0^4 f (t)dt = 7.$
Nên: $int_0^4 f (t)dt$ $ = int_0^3 f (t)dt + int_3^4 f (t)dt$ $ Leftrightarrow 7 = 3 + int_3^4 f (t)dt.$
Vậy $int_3^4 f (t)dt = 4.$Bài 13.
a) Chứng minh rằng nếu $f(x) > 0$ trên $[a;b]$ thì $int_a^b f (x)dx > 0.$
b) Chứng minh rằng nếu $f(x) > g(x)$ trên $[a;b]$ thì $int_a^b f (x)dx > int_a^b g (x)dx.$Lời giải:
a) Gọi $F(x)$ là một nguyên hàm của $f(x)$, ta có: $F'(x) = f(x) > 0$ trên đoạn $[a;b].$ Do đó $F(x)$ tăng trên đoạn $[a;b].$
Vì vậy $a < b$ $ Rightarrow F(a) < F(b).$
Nên $int_a^b f (x)dx = F(b) – F(a) > 0.$
b) Theo câu a ta có: $f(x) – g(x) > 0$ nên:
$int_a^b {(f(} x) – g(x))dx > 0$ $ Leftrightarrow int_a^b f (x)dx – int_a^b g (x)dx > 0.$
Vậy $int_a^b f (x)dx > int_a^b g (x)dx.$Bài 14.
a) Một vật chuyển động với vận tốc $v(t) = 1 – 2sin 2t$ $(m/s).$ Tính quãng đường vật di chuyển trong khoảng thời gian từ thời điểm $t = 0$ $(s)$ đến thời điểm $t = frac{{3pi }}{4}$ $(s).$
b) Một vật chuyển động chậm dần với vận tốc $v(t) = 160 – 10t$ $(m/s).$ Tính quãng đường mà vật di chuyển được từ thời điểm $t = 0$ đến thời điểm mà vật dừng lại.Lời giải:
a) Quãng đường $S$ đi được từ $t = 0$ $(s)$ đến $t = frac{{3pi }}{4}$ $(s)$ là $S = int_0^{3pi /4} {(1 – 2sin 2t)dt} $ $ = left. {(t + cos 2t)} right|_0^{3pi /4}$ $ = frac{{3pi }}{4} – 1.$
b) Khi vật dừng lại thì $v(t) = 0$ $ Leftrightarrow 160 – 10t = 0$ $ Leftrightarrow t = 16$ $(s).$
Vậy quãng đường đi được từ $t = 0$ đến khi dừng lại là:
$S = int_0^{16} {(160 – 10t)dt} $ $ = left. {left( {160t – 5{t^2}} right)} right|_0^{16}$ $ = 1280$ $(m).$Bài 15. Một vật chuyển động với vận tốc $10$ $m/s$ thì tăng tốc với gia tốc $a(t) = 3t + {t^2}.$ Tính quãng đường vật đi được trong khoảng thời gian $10$ giây kể từ lúc bắt đầu tăng tốc.Lời giải:
Chọn mốc thời gian vật bắt đầu tăng tốc ${t_0} = 0.$
Lúc đó vận tốc trong khoảng ${t_0} = 0$ đến $T$ là:
$v(T) = int_0^T {left( {3t + {t^2}} right)dt} $ $ = frac{{{T^3}}}{3} + frac{3}{2}{T^2}$ $ Rightarrow $ Vận tốc tăng: $V(t) = frac{{{t^3}}}{3} + frac{3}{2}{t^2} + 10.$
Quãng đường đi được từ khi tăng tốc trong $10$ giây là:
$S = int_0^{10} {left( {frac{{{t^3}}}{3} + frac{3}{2}{t^2} + 10} right)dt} $ $ = left. {left( {frac{{{t^4}}}{{12}} + frac{1}{2}{t^3} + 10t} right)} right|_0^{10}$ $ = frac{{4300}}{3}$ $(m).$
Vậy quãng đường đi được là $frac{{4300}}{3}$ $(m).$Bài 16. Một viên đạn được bắn lên theo phương thẳng đứng với vận tốc ban đầu $25$ $m/s.$ Gia tốc trọng trường là $9,8$ $m/{s^2}.$
a) Sau bao lâu viên đạn đạt tới tốc độ cao lớn nhất.
b) Tính quãng đường viên đạn đi được từ lúc bắn lên cho đến khi rơi xuống đất (chính xác đến hàng phần trăm).Lời giải:
a) Giả sử rằng đạn được bắn lên từ mặt đất, khi đó:
$v(t) = {v_o} – gt$ $ = 25 – 9,8t$ ($t ge 0$, $t$ tính bằng giây).
Ta đã biết quãng đường viên đạn đi được trong $t$ giây là $S(t)$ thì:
$S'(t) = v(t)$ $ Rightarrow S(t) = int v (t)dt$ $ = int {(25 – 9,8t)dt} .$
$ Rightarrow S(t) = 25t – 4,9{t^2} + C$ ($S(t)$ tính bằng mét).
Vì viên đạn được bắn lên từ mặt đất cho nên $S(0) = 0$, vì vậy $C = 0.$
Từ đó: $S(t) = 25t – 4,9{t^2}$ $(1).$
Ta có: $(1) Leftrightarrow S(t) = – 4,9{t^2} + 25t.$
$ Leftrightarrow S(t) = – 4,9{left( {t – frac{{25}}{{9,8}}} right)^2} + frac{{625}}{{19,6}}.$
$ Rightarrow S(t) le frac{{625}}{{19,6}}$, $forall t ge 0$, dấu bằng xảy ra khi và chỉ khi: $t = frac{{25}}{{9,8}}.$
Do đó: $mathop {max }limits_{[0; + infty )} S(t) = frac{{625}}{{19,6}}$ khi $t = frac{{25}}{{9,8}}.$
Vì thế, sau thời gian $t = frac{{25}}{{9,8}}$ (giây) thì viên đạn đạt độ cao lớn nhất là:
$h = mathop {max }limits_{[0; + infty )} S(t) = frac{{625}}{{19,6}}$ (mét).
b) Quãng đường mà viên đạn đi được từ khi bắn lên cho đến khi rơi xuống đất là: $2h = 2max S(t)$ $ = frac{{1250}}{{19,6}} approx 63,78$ (mét).
Để lại một phản hồi