Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Hình học 12 cơ bản: Phương trình đường thẳng trong không gian.CÂU HỎI VÀ BÀI TẬPBài 1. Viết phương trình tham số của đường thẳng $d$ trong mỗi trường hợp sau:
a) $d$ đi qua điểm $M(5; 4; 1)$ và có vectơ chỉ phương $overrightarrow a = (2; – 3;1).$
b) $d$ đi qua điểm $A(2; -1; 3)$ và vuông góc với mặt phẳng $(alpha )$ có phương trình $x + y – z + 5 = 0.$
c) $d$ đi qua điểm $B(2;0; -3)$ và song song với đường thẳng $Delta :left{ {begin{array}{*{20}{l}}
{x = 1 + 2t}\
{y = – 3 + 3t}\
{z = 4t}
end{array}} right..$
d) $d$ đi qua hai điểm $P(1;2;3)$ và $Q(5;4;4).$Lời giải:
a) $d$ đi qua điểm $M(5; 4; 1)$ và có vectơ chỉ phương $vec a = (2; – 3;1)$ nên $d$ có phương trình: $left{ {begin{array}{*{20}{l}}
{x = 5 + 2t}\
{y = 4 – 3t}\
{z = 1 + t}
end{array}} right..$
b) Do $d$ vuông góc với mặt phẳng $(alpha ):x + y – z + 5 = 0$, nên $d$ nhận vectơ $overrightarrow a = (1;1; – 1)$ làm vectơ chỉ phương.
Do vậy $d$ có phương trình: $left{ {begin{array}{*{20}{l}}
{x = 2 + t}\
{y = – 1 + t}\
{z = 3 – t}
end{array}} right..$
c) Do $d$ song song với đường thẳng $Delta :left{ {begin{array}{*{20}{l}}
{x = 1 + 2t}\
{y = – 3 + 3t}\
{z = 4t}
end{array}} right.$ nên $d$ nhận vectơ $overrightarrow a = (2;3;4)$ làm vectơ chỉ phương, mà $d$ đi qua $B(2;0; – 3).$
Do đó $d$ có phương trình: $left{ {begin{array}{*{20}{l}}
{x = 2 + 2t}\
{y = 3t}\
{z = – 3 + 4t}
end{array}} right..$
d) Do $d$ đi qua $P(1;2;3)$ và $Q(5;4;4)$ nên $d$ nhận vectơ $overrightarrow {PQ} = (4;2;1)$ làm vectơ chỉ phương. Do đó $d$ có phương trình: $left{ {begin{array}{*{20}{l}}
{x = 1 + 4t}\
{y = 2 + 2t}\
{z = 3 + t}
end{array}} right..$Bài 2. Viết phương trình tham số của đường thẳng là hình chiếu vuông góc của đường thẳng $d:left{ {begin{array}{*{20}{l}}
{x = 2 + t}\
{y = – 3 + 2t}\
{z = 1 + 3t}
end{array}} right.$ lần lượt trên các mặt phẳng sau:
a) $(Oxy).$
b) $(Oyz).$Lời giải:
a) Gọi $(P)$ là mặt phẳng chứa $d$ và vuông góc với mặt phẳng $(Oxy).$
Suy ra $(P)$ nhận vectơ $vec n = vec k wedge vec a$ ($overrightarrow k = (0;0;1)$, $overrightarrow a = (1;2;3)$) làm vectơ pháp tuyến.
Mà $vec n = left( {left| {begin{array}{*{20}{c}}
0&1\
2&3
end{array}} right|;left| {begin{array}{*{20}{c}}
1&0\
3&1
end{array}} right|;left| {begin{array}{*{20}{c}}
0&0\
1&2
end{array}} right|} right)$ $ = ( – 2;1;0).$
$(P)$ đi qua $A(2; -3; 1)$, nên $(P)$ có phương trình: $ – 2(x – 2) + 1(y + 3) + 0(z – 1) = 0$ hay $2x – y – 7 = 0.$
Suy ra hình chiếu của đường thẳng $d$ lên $(Oxy)$ có phương trình $left{ {begin{array}{*{20}{l}}
{2x – y – 7 = 0}\
{z = 0}
end{array}} right.$ hay $d$ có vectơ chỉ phương $overrightarrow u = left( {left| {begin{array}{*{20}{c}}
{ – 1}&0\
0&1
end{array}} right|;left| {begin{array}{*{20}{c}}
0&2\
1&0
end{array}} right|;left| {begin{array}{*{20}{c}}
2&{ – 1}\
0&0
end{array}} right|} right)$ $ = ( – 1; – 2;0).$
Mà $d$ đi qua $B(2; -3; 0).$
Suy ra $d$ có phương trình tham số: $left{ {begin{array}{*{20}{l}}
{x = 2 – t}\
{y = – 3 – 2t}\
{z = 0}
end{array}} right..$
b) Hoàn toàn tương tự ta có phương trình tham số của $d$ trên mặt phẳng $(Oyz)$ là: $left{ {begin{array}{*{20}{l}}
{x = 0}\
{y = – 3 + 2t}\
{z = 1 + 3t}
end{array}.} right.$Bài 3. Xét vị trí tương đối của các cặp đường thẳng $d$ và $d’$ cho bởi các phương trình sau:
a) $d:left{ {begin{array}{*{20}{l}}
{x = – 3 + 2t}\
{y = – 2 + 3t}\
{z = 6 + 4t}
end{array}} right.$ và $d’:left{ {begin{array}{*{20}{l}}
{x = 5 + t’}\
{y = – 1 – 4t’}\
{z = 20 + t’}
end{array}} right..$
b) $d:left{ {begin{array}{*{20}{l}}
{x = 1 + t}\
{y = 2 + t}\
{z = 3 – t}
end{array}} right.$ và $d’:left{ {begin{array}{*{20}{l}}
{x = 1 + 2t’}\
{y = – 1 + 2t’}\
{z = 2 – 2t’}
end{array}.} right.$Lời giải:
a) Xét hệ phương trình: $left{ {begin{array}{*{20}{l}}
{ – 3 + 2t = 5 + t’}\
{ – 2 + 3t = – 1 – 4t’}\
{6 + 4t = 20 + t’}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{2t – t’ = 8}\
{3t + 4t’ = 1}\
{4t – t’ = 14}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{t = 3}\
{t’ = – 2}
end{array}} right..$
Suy ra hệ có nghiệm $left{ {begin{array}{*{20}{l}}
{{t_0} = 3}\
{t{‘_0} = – 2}
end{array}} right..$
Nên $d$ cắt $d’$ tại điểm ${M_0}(3;7;18).$
b) Xét hệ phương trình:
$left{ {begin{array}{*{20}{l}}
{1 + t = 1 + 2t’}\
{2 + t = – 1 + 2t’}\
{3 – t = 2 – 2t’}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{t – 2t’ = 0}\
{t – 2t’ = – 3}\
{t – 2t’ = 1}
end{array}} right.$, suy ra hệ vô nghiệm.
Lại có $d$ nhận $vec a = (1;1; – 1)$ làm vectơ chỉ phương, $d’$ nhận $overrightarrow {a’} = (2;2; – 2)$ làm vectơ chỉ phương.
Mà $overrightarrow {a’} = 2vec a$ $ Rightarrow d$ và $d’$ là hai đường thẳng song song.Bài 4. Tìm $a$ để hai đường thẳng sau đây cắt nhau:
$d:left{ {begin{array}{*{20}{l}}
{x = 1 + at}\
{y = t}\
{z = – 1 + 2t}
end{array}} right.$ và $d’:left{ {begin{array}{*{20}{l}}
{x = 1 – t’}\
{y = 2 + 2t’}\
{z = 3 – t’}
end{array}.} right.$Lời giải:
Xét hệ phương trình:
$left{ {begin{array}{*{20}{l}}
{1 + at = 1 – t’}\
{t = 2 + 2t’}\
{ – 1 + 2t = 3 – t’}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{t’ + at = 0}\
{t = 2 + 2t’}\
{ – 1 + 2left( {2 + 2t’} right) = 3 – t’}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{t’ + at = 0}\
{t’ = 0}\
{t = frac{6}{5}}
end{array}} right..$
Để $d$ và $d’$ cắt nhau thì hệ phải có nghiệm duy nhất $t$ và $t’$ $ Rightarrow 0 + frac{6}{5}a = 0$ $ Leftrightarrow a = 0.$
Vậy $a = 0$ là giá trị cần tìm.Bài 5. Tìm số giao điểm của đường thẳng $d$ với mặt phẳng $(alpha )$ trong các trường hợp sau:
a) $d:left{ {begin{array}{*{20}{l}}
{x = 12 + 4t}\
{y = 9 + 3t}\
{z = 1 + t}
end{array}} right.$ và $3x + 5y – z – 2 = 0.$
b) $d:left{ {begin{array}{*{20}{l}}
{x = 1 + t}\
{y = 2 – t}\
{z = 1 + 2t}
end{array}} right.$ và $(alpha ):x + 3y + z + 1 = 0.$
c) $d:left{ {begin{array}{*{20}{l}}
{x = 1 + t}\
{y = 1 + 2t}\
{z = 2 – 3t}
end{array}} right.$ và $(alpha ):x + y + z – 4 = 0.$Lời giải:
a) Xét phương trình: $3(12 + 4t) + 5(9 + 3t) – (1 + t) – 2 = 0.$
$ Leftrightarrow 26t + 78 = 0$ $ Leftrightarrow t = – 3$ là nghiệm duy nhất.
Suy ra đường thẳng $d$ cắt mặt phẳng $(alpha )$ tại điểm $A(0;0; – 2).$
b) Xét phương trình: $(1 + t) + 3(2 – t) + (1 + 2t) + 1 = 0$ $ Leftrightarrow 9 = 0$ vô lý.
Suy ra $d//(alpha ).$ Vậy $d$ và $(alpha )$ không có điểm chung.
c) Xét phương trình: $(1 + t) + (1 + 2t) + (2 – 3t) – 4 = 0$ $ Leftrightarrow 4 – 4 = 0$ đúng với mọi $t$ $ Rightarrow d$ nằm trong mặt phẳng $(alpha ).$ Vậy $d$ và $(alpha )$ có vô số điểm chung.Bài 6. Tính khoảng cách giữa đường thẳng $Delta :left{ {begin{array}{*{20}{l}}
{x = – 3 + 2t}\
{y = – 1 + 3t}\
{z = – 1 + 2t}
end{array}} right.$ và mặt phẳng $(alpha ):2x – 2y + z + 3 = 0.$Lời giải:
Xét phương trình: $2( – 3 + 2t) – 2( – 1 + 3t) + ( – 1 + 2t) + 3 = 0$ $ Leftrightarrow 2 = 0$ vô lý $ Rightarrow Delta //(alpha ).$
Lại có $Delta $ đi qua điểm $A( – 3; – 1; – 1).$
$ Rightarrow d(Delta ,(alpha )) = d(A,(alpha ))$ $ = frac{{|2.( – 3) – 2( – 1) – 1 + 3|}}{{sqrt {{2^2} + {{( – 2)}^2} + {1^2}} }}$ $ = frac{2}{3}.$
Vậy khoảng cách giữa $Delta $ và $(alpha )$ là $frac{2}{3}$ (đvđd).Bài 7. Cho điểm $A(1; 0; 0)$ và đường thẳng $Delta :left{ {begin{array}{*{20}{l}}
{x = 2 + t}\
{y = 1 + 2t}\
{z = t}
end{array}} right..$
a) Tìm tọa độ điểm $H$ là hình chiếu vuông góc của điểm $A$ trên đường thẳng $Delta .$
b) Tìm tọa độ điểm $A’$ đối xứng với $A$ qua đường thẳng $Delta .$Lời giải:
a) Gọi $(alpha )$ là mặt phẳng qua $A$ và vuông góc với $Delta $, suy ra mặt phẳng $(alpha )$ nhận $overrightarrow n = (1;2;1)$ làm vectơ pháp tuyến.
$ Rightarrow (alpha )$ có phương trình $1(x – 1) + 2y + z = 0$ hay $x + 2y + z – 1 = 0.$
Suy ra tọa độ điểm $H$ là hình chiếu vuông góc của điểm $A$ trên đường thẳng $Delta $ là nghiệm hệ:
$left{ {begin{array}{*{20}{l}}
{x = 2 + t}\
{y = 1 + 2t}\
{z = t}\
{x + 2y + z – 1 = 0}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{x = 2 + t}\
{y = 1 + 2t}\
{z = t}\
{(2 + t) + 2(1 + 2t) + t – 1 = 0}
end{array}} right.$ $left{ {begin{array}{*{20}{l}}
{t = – frac{1}{2}}\
{x = frac{3}{2}}\
{y = 0}\
{z = – frac{1}{2}}
end{array}} right..$
Vậy $Hleft( {frac{3}{2};0; – frac{1}{2}} right).$
b) Gọi $A’$ là điểm đối xứng với $A$ qua $Delta .$ Theo câu a, suy ra $H$ là trung điểm của $AA’$, suy ra tọa độ của $A’$ là:
$left{ {begin{array}{*{20}{l}}
{{x_{A’}} = 2{x_H} – {x_A}}\
{{y_{A’}} = 2{y_H} – {y_A}}\
{{z_{A’}} = 2{z_H} – {z_A}}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{{x_{A’}} = 2}\
{{y_{A’}} = 0}\
{{z_{A’}} = – 1}
end{array}} right..$ Vậy $A(2; 0; -1).$Bài 8. Cho điểm $M(1; 4; 2)$ và mặt phẳng $(alpha ):x + y + z – 1 = 0.$
a) Tìm tọa độ điểm $H$ là hình chiếu vuông góc của điểm $M$ trên mặt phẳng $(alpha ).$
b) Tìm tọa độ điểm $M’$ đối xứng với $M$ qua mặt phẳng $(alpha ).$
c) Tính khoảng cách từ điểm $M$ đến mặt phẳng $(alpha ).$Lời giải:
a) Gọi $Delta $ là đường thẳng đi qua $M$ và vuông góc với $(alpha )$, suy ra $Delta $ nhận vectơ $overrightarrow a = (1;1;1)$ làm vectơ chỉ phương.
Suy ra $Delta $ có phương trình: $left{ {begin{array}{*{20}{l}}
{x = 1 + t}\
{y = 4 + t}\
{z = 2 + t}
end{array}} right..$
Suy ra tọa độ điểm $H$ là hình chiếu vuông góc của điểm $M$ trên $(alpha )$, là nghiệm của hệ:
$left{ {begin{array}{*{20}{l}}
{x = 1 + t}\
{y = 4 + t}\
{z = 2 + t}\
{x + y + z – 1 = 0}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{x = 1 + t}\
{y = 4 + t}\
{z = 2 + t}\
{(1 + t) + (4 + t) + (2 + t) – 1 = 0}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{t = – 2}\
{x = – 1}\
{y = 2}\
{z = 0}
end{array}} right..$
Vậy $H = ( – 1;2;0).$
b) Gọi $M’ = (x;y;z)$ là điểm đối xứng của $M$ qua mặt phẳng $(alpha ).$
Suy ra $M$ và $M’$ đối xứng nhau qua điểm $H$, hay $H$ là trung điểm của $MM’.$
$ Rightarrow left{ {begin{array}{*{20}{l}}
{x = 2{x_H} – {x_M}}\
{y = 2{y_H} – {y_M}}\
{z = 2{z_H} – {z_M}}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{x = – 3}\
{y = 0}\
{z = – 2}
end{array}} right..$ Vậy $M’ = ( – 3;0; – 2).$
c) Khoảng cách từ điểm $M$ đến mặt phẳng $(alpha )$ là:
$d(M,(alpha ))$ $ = frac{{|1 + 4 + 2 – 1|}}{{sqrt {{1^2} + {1^2} + {1^2}} }}$ $ = frac{6}{{sqrt 3 }} = 2sqrt 3 $ (đvđd).
Chú ý: Ta có thể tính: $d(M,(alpha )) = MH$ $ = |overrightarrow {MH} | = 2sqrt 3 .$Bài 9. Cho hai đường thẳng $d:left{ {begin{array}{*{20}{l}}
{x = 1 – t}\
{y = 2 + 2t}\
{z = 3t}
end{array}} right.$ và $d’:left{ {begin{array}{*{20}{l}}
{x = 1 + t}\
{y = 3 – 2t}\
{z = 1}
end{array}} right..$
Chứng minh $d$ và $d’$ chéo nhau.Lời giải:
Cách 1. Ta có $d$ có vectơ chỉ phương $vec a = ( – 1;2;3)$ và đi qua điểm $M(1; 2; 0)$, $d’$ có vectơ chỉ phương $overrightarrow {a’} = (1; – 2;0)$ và đi qua điểm $M'(1; 3; 1).$
$ Rightarrow overrightarrow a $ và $overrightarrow {a’} $ không cùng phương $(1).$
Lại có, xét hệ phương trình: $left{ {begin{array}{*{20}{l}}
{1 – t = 1 + t’}\
{2 + 2t = 3 – 2t’}\
{3t = 1}
end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}}
{t = frac{1}{3}}\
{t = – t’}\
{2t = – 2t’ + 1}
end{array}} right.$ vô lý $(2).$
Từ $(1)$ và $(2)$ suy ra $d$ và $d’$ chéo nhau.
Cách 2. Ta có $overrightarrow {MM’} = (0;1;1).$
$overrightarrow a wedge overrightarrow {a’} $ $ = left( {left| {begin{array}{*{20}{c}}
2&3\
{ – 2}&0
end{array}} right|;left| {begin{array}{*{20}{c}}
3&{ – 1}\
0&1
end{array}} right|;left| {begin{array}{*{20}{c}}
{ – 1}&2\
1&{ – 2}
end{array}} right|} right)$ $ = (6;3;0).$
$ Rightarrow left( {overrightarrow a wedge overrightarrow {a’} } right).overrightarrow {MM’} $ $ = 6.0 + 1.3 + 0.1 = 3 ne 0.$
Suy ra $overrightarrow a $, $overrightarrow {a’} $, $overrightarrow {MM’} $ không đồng phẳng, hay $d$ và $d’$ chéo nhau.Bài 10. Giải bài toán sau đây bằng phương pháp tọa độ:
Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $1.$ Tính khoảng cách từ đỉnh $A$ đến các mặt phẳng $(A’BD)$ và $(B’D’C).$Lời giải:
Chọn hệ trục tọa độ như hình vẽ: $A = O(0;0;0)$, $B(1;0;0)$, $D(0;1;0)$, $A'(0;0;1).$
Suy ra $C = (1;1;0)$, $B’ = (1;0;1)$, $D’ = (0;1;1).$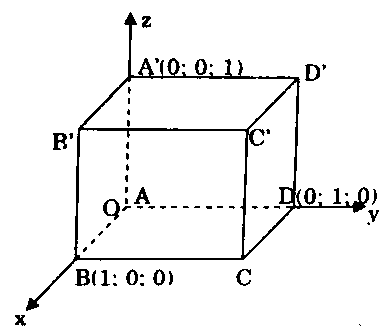
Ta có $overrightarrow {A’B} = (1;0; – 1)$, $overrightarrow {A’D} = (0;1; – 1).$
$ Rightarrow overrightarrow {A’B} wedge overrightarrow {A’D} $ $ = left( {left| {begin{array}{*{20}{r}}
0&{ – 1}\
1&{ – 1}
end{array}} right|;left| {begin{array}{*{20}{r}}
{ – 1}&1\
{ – 1}&0
end{array}} right|;left| {begin{array}{*{20}{l}}
1&0\
0&1
end{array}} right|} right)$ $ = (1;1;1).$
Suy ra mặt phẳng $(A’BD)$ có phương trình $1(x – 0) + 1(y – 0) + 1(z – 1) = 0$ hay $x + y + z – 1 = 0.$
Khoảng cách từ đỉnh $A$ đến $(A’BD)$ là: $dleft( {A,left( {A’BD} right)} right)$ $ = frac{{|0 + 0 + 0 – 1|}}{{sqrt {{1^2} + {1^2} + {1^2}} }}$ $ = frac{1}{{sqrt 3 }}$ (đvđd).
Ta có $overrightarrow {B’D’} = ( – 1;1;0)$, $overrightarrow {B’C} = (0;1; – 1).$
$ Rightarrow overrightarrow {B’D’} wedge overrightarrow {B’C} $ $ = left( {left| {begin{array}{*{20}{r}}
1&0\
1&{ – 1}
end{array}} right|;left| {begin{array}{*{20}{r}}
0&{ – 1}\
{ – 1}&0
end{array}} right|;left| {begin{array}{*{20}{c}}
{ – 1}&1\
0&1
end{array}} right|} right)$ $ = ( – 1; – 1; – 1).$
Suy ra $left( {B’D’C} right)$ có phương trình: $ – 1(x – 1) – 1(y – 0) – 1(z – 1) = 0$ hay $x + y + z – 2 = 0.$
Suy ra khoảng cách từ đỉnh $A$ đến $(B’D’C)$ là: $dleft( {A,left( {B’D’C} right)} right)$ $ = frac{{|0 + 0 + 0 – 2|}}{{sqrt {{1^2} + {1^2} + {1^2}} }}$ $ = frac{2}{{sqrt 3 }}$ (đvđd).
Để lại một phản hồi